名校
1 . 在 中,
中, 的平分线交AC于点D,
的平分线交AC于点D,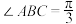 ,
,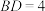 ,则
,则 面积的最小值为( )
面积的最小值为( )
 中,
中, 的平分线交AC于点D,
的平分线交AC于点D,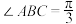 ,
,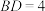 ,则
,则 面积的最小值为( )
面积的最小值为( )A.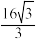 | B.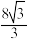 | C.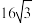 | D.16 |
您最近半年使用:0次
2024高三·全国·专题练习
解题方法
2 . 已知 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且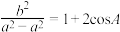 ,
, ,
, 的面积
的面积 ,则
,则 ( )
( )
 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且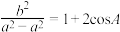 ,
, ,
, 的面积
的面积 ,则
,则 ( )
( )A. | B.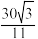 | C. 或 或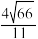 | D.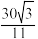 或 或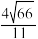 |
您最近半年使用:0次
解题方法
3 . 设 ,函数
,函数 图象的两条相邻对称轴之间的距离为
图象的两条相邻对称轴之间的距离为 .
.
(1)求函数 的解析式;
的解析式;
(2)在 中,设角
中,设角 、
、 及
及 所对边的边长分别为
所对边的边长分别为 、
、 及
及 ,若
,若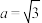 ,
, ,
,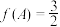 ,求角
,求角 .
.
 ,函数
,函数 图象的两条相邻对称轴之间的距离为
图象的两条相邻对称轴之间的距离为 .
.(1)求函数
 的解析式;
的解析式;(2)在
 中,设角
中,设角 、
、 及
及 所对边的边长分别为
所对边的边长分别为 、
、 及
及 ,若
,若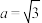 ,
, ,
,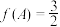 ,求角
,求角 .
.
您最近半年使用:0次
名校
4 . 已知函数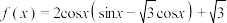 .
.
(1)求 的最小正周期和
的最小正周期和 的单调递减区间;
的单调递减区间;
(2)当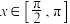 时,求函数
时,求函数 的值域及取得最小值时x的值.
的值域及取得最小值时x的值.
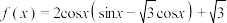 .
.(1)求
 的最小正周期和
的最小正周期和 的单调递减区间;
的单调递减区间;(2)当
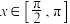 时,求函数
时,求函数 的值域及取得最小值时x的值.
的值域及取得最小值时x的值.
您最近半年使用:0次
解题方法
5 . 在锐角 中,内角
中,内角 ,
, ,
, 所对边分别为
所对边分别为 ,
, ,
, ,
,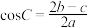 .
.
(1)求角 ;
;
(2)设 是角
是角 的平分线,与
的平分线,与 边交于
边交于 ,若
,若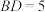 ,
,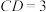 ,求
,求 ,
, ;
;
(3)若 ,求
,求 面积的取值范围.
面积的取值范围.
 中,内角
中,内角 ,
, ,
, 所对边分别为
所对边分别为 ,
, ,
, ,
,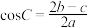 .
.(1)求角
 ;
;(2)设
 是角
是角 的平分线,与
的平分线,与 边交于
边交于 ,若
,若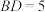 ,
,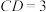 ,求
,求 ,
, ;
;(3)若
 ,求
,求 面积的取值范围.
面积的取值范围.
您最近半年使用:0次
名校
6 . 已知函数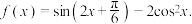
(1)求 的最小正周期;
的最小正周期;
(2)求 的最大值及取得最大值时x的取值集合.
的最大值及取得最大值时x的取值集合.
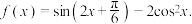
(1)求
 的最小正周期;
的最小正周期;(2)求
 的最大值及取得最大值时x的取值集合.
的最大值及取得最大值时x的取值集合.
您最近半年使用:0次
7 . 已知向量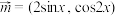 ,
,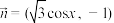 ,函数
,函数
(1)求 的单调递减区间;
的单调递减区间;
(2)在 中,内角A,B,C所对的边分别为a,b,c,若
中,内角A,B,C所对的边分别为a,b,c,若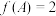 ,
,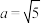 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
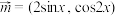 ,
,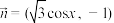 ,函数
,函数
(1)求
 的单调递减区间;
的单调递减区间;(2)在
 中,内角A,B,C所对的边分别为a,b,c,若
中,内角A,B,C所对的边分别为a,b,c,若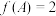 ,
,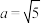 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
您最近半年使用:0次
8 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A.函数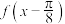 为奇函数 为奇函数 |
B.曲线 的对称轴为 的对称轴为 , ,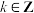 |
C. 在 在 上单调递增 上单调递增 |
D. 在 在 处取得极小值 处取得极小值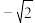 |
您最近半年使用:0次
解题方法
9 . 已知 的内角A,B,C的对边分别为a,b,c,且
的内角A,B,C的对边分别为a,b,c,且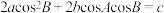 .
.
(1)求B;
(2)若 ,
, 的面积为S.周长为L,求
的面积为S.周长为L,求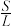 的最大值.
的最大值.
 的内角A,B,C的对边分别为a,b,c,且
的内角A,B,C的对边分别为a,b,c,且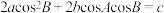 .
.(1)求B;
(2)若
 ,
, 的面积为S.周长为L,求
的面积为S.周长为L,求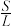 的最大值.
的最大值.
您最近半年使用:0次
7日内更新
|
197次组卷
|
2卷引用:青海省部分学校2023-2024学年高三下学期联考模拟预测理科数学试题
解题方法
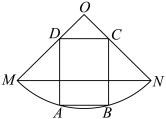
10 . 如图,有一块半径为1,圆心角为 的扇形木块
的扇形木块 ,现要分割出一块矩形
,现要分割出一块矩形 ,其中点
,其中点 ,
, 在弧
在弧 上,且线段
上,且线段 平行于线段
平行于线段 .
. ,
, 分别为弧
分别为弧 的两个三等分点,求矩形
的两个三等分点,求矩形 的面积
的面积 ;
;
(2)设
 ,当
,当 为何值时,矩形
为何值时,矩形 的面积
的面积 最大?最大值为多少?
最大?最大值为多少?
 的扇形木块
的扇形木块 ,现要分割出一块矩形
,现要分割出一块矩形 ,其中点
,其中点 ,
, 在弧
在弧 上,且线段
上,且线段 平行于线段
平行于线段 .
.
 ,
, 分别为弧
分别为弧 的两个三等分点,求矩形
的两个三等分点,求矩形 的面积
的面积 ;
;(2)设

 ,当
,当 为何值时,矩形
为何值时,矩形 的面积
的面积 最大?最大值为多少?
最大?最大值为多少?
您最近半年使用:0次
7日内更新
|
214次组卷
|
2卷引用:湖北省宜荆荆随恩重点高中教研协作体2023-2024学年高一下学期3月联考数学试卷



