名校
1 . 已知函数 ,把
,把 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则( )
的图象,则( )
 ,把
,把 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则( )
的图象,则( )A. 是偶函数 是偶函数 | B. 的图象关于直线 的图象关于直线 对称 对称 |
C. 的图象关于直线 的图象关于直线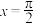 对称 对称 | D. 的图象关于点 的图象关于点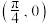 中心对称 中心对称 |
您最近半年使用:0次
2 . 已知函数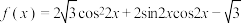 ,则下列结论正确的是( )
,则下列结论正确的是( )
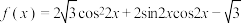 ,则下列结论正确的是( )
,则下列结论正确的是( )A.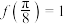 | B. 在 在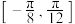 上单调递增 上单调递增 |
C. 的值域为 的值域为 | D.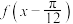 的图象关于直线 的图象关于直线 对称 对称 |
您最近半年使用:0次
3 . 若函数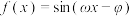 (
( ,
, )的最小正周期为
)的最小正周期为 ,且
,且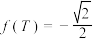 ,若
,若 在区间
在区间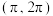 内没有零点,则
内没有零点,则 的取值范围为
的取值范围为_________ .
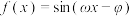 (
( ,
, )的最小正周期为
)的最小正周期为 ,且
,且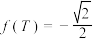 ,若
,若 在区间
在区间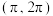 内没有零点,则
内没有零点,则 的取值范围为
的取值范围为
您最近半年使用:0次
4 . 函数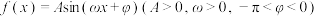 的部分图象如图所示,则( )
的部分图象如图所示,则( )
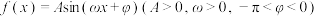 的部分图象如图所示,则( )
的部分图象如图所示,则( )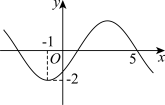
A. |
B. |
C. 的图象关于点 的图象关于点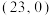 对称 对称 |
D.不等式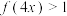 的解集为 的解集为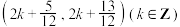 |
您最近半年使用:0次
解题方法
5 . 已知函数 ,其中
,其中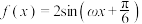 ,实数
,实数 ,下列选项中正确的是( )
,下列选项中正确的是( )
 ,其中
,其中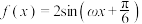 ,实数
,实数 ,下列选项中正确的是( )
,下列选项中正确的是( )A.若 ,函数 ,函数 关于直线 关于直线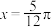 对称 对称 |
B.若 ,函数 ,函数 在 在 上是增函数 上是增函数 |
C.若函数 在 在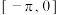 上最大值为1,则 上最大值为1,则 |
D.若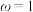 ,则函数 ,则函数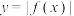 的最小正周期是 的最小正周期是 |
您最近半年使用:0次
6 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A.函数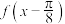 为奇函数 为奇函数 |
B.曲线 的对称轴为 的对称轴为 , ,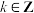 |
C. 在 在 上单调递增 上单调递增 |
D. 在 在 处取得极小值 处取得极小值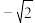 |
您最近半年使用:0次
7 . 已知函数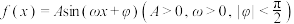 的部分图象如图所示,若
的部分图象如图所示,若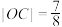 ,
, ,则( )
,则( )
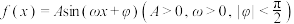 的部分图象如图所示,若
的部分图象如图所示,若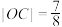 ,
, ,则( )
,则( )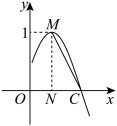
A.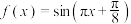 |
B. 的单调递增区间为 的单调递增区间为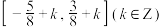 |
C. 图象关于点 图象关于点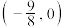 对称 对称 |
D. 图象关于直线 图象关于直线 对称 对称 |
您最近半年使用:0次
解题方法
8 . 已知函数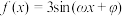 (
( ,
, )的部分图象如图所示,则下列说法正确的是( )
)的部分图象如图所示,则下列说法正确的是( )
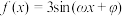 (
( ,
, )的部分图象如图所示,则下列说法正确的是( )
)的部分图象如图所示,则下列说法正确的是( )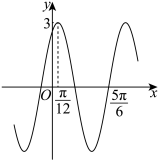
A.函数 的解析式 的解析式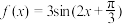 |
B.直线 是函数 是函数 图象的一条对称轴 图象的一条对称轴 |
C. 在区间 在区间 上单调递增 上单调递增 |
D.不等式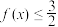 的解集为 的解集为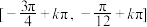 , ,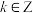 |
您最近半年使用:0次
名校
9 . 已知函数 ,其中
,其中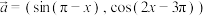 ,
,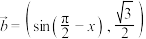 ,
, .
.
(1)求函数 的最小正周期和对称轴;
的最小正周期和对称轴;
(2)求函数 在
在 上的单调递减区间;
上的单调递减区间;
(3)已知函数 在
在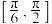 上存在零点,求实数
上存在零点,求实数 的取值范围.
的取值范围.
 ,其中
,其中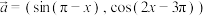 ,
,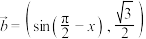 ,
, .
.(1)求函数
 的最小正周期和对称轴;
的最小正周期和对称轴;(2)求函数
 在
在 上的单调递减区间;
上的单调递减区间;(3)已知函数
 在
在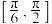 上存在零点,求实数
上存在零点,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
名校
10 . 已知函数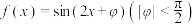 ,若把函数
,若把函数 的图像向右平移
的图像向右平移 个单位长度后得到的图像关于原点对称,则( )
个单位长度后得到的图像关于原点对称,则( )
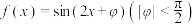 ,若把函数
,若把函数 的图像向右平移
的图像向右平移 个单位长度后得到的图像关于原点对称,则( )
个单位长度后得到的图像关于原点对称,则( )A.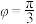 |
B.函数 的图象关于点 的图象关于点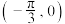 对称 对称 |
C.函数 在区间 在区间 上单调递减 上单调递减 |
D.函数 在 在 上有2个零点 上有2个零点 |
您最近半年使用:0次



