1 . 已知函数 ,则( )
,则( )
 ,则( )
,则( )A. 的图象关于直线 的图象关于直线 对称 对称 |
B. 是周期函数,且其中一个周期是 是周期函数,且其中一个周期是 |
C. 的值域是 的值域是 |
D. 在 在 上单调递增 上单调递增 |
您最近一年使用:0次
2 . 设函数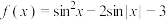 ,则( )
,则( )
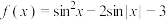 ,则( )
,则( )A. 是偶函数 是偶函数 | B. 在 在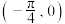 上单调递减 上单调递减 |
C. 的最小值是 的最小值是 | D. 在 在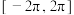 上有 上有 个零点 个零点 |
您最近一年使用:0次
3 . 已知函数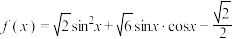 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)求函数 在区间
在区间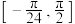 上的值域.
上的值域.
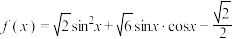 .
.(1)求函数
 的单调递增区间;
的单调递增区间;(2)求函数
 在区间
在区间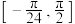 上的值域.
上的值域.
您最近一年使用:0次
4 . 已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 的单调递减区间.
的单调递减区间.
 .
.(1)求
 的最小正周期;
的最小正周期;(2)求
 的单调递减区间.
的单调递减区间.
您最近一年使用:0次
5 . 已知函数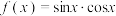 ,则( )
,则( )
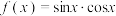 ,则( )
,则( )A. 是奇函数 是奇函数 | B. 的最小正周期为 的最小正周期为 |
C. 的最小值为 的最小值为 | D. 在 在 上单调递增 上单调递增 |
您最近一年使用:0次
6 . 函数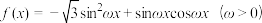 .若
.若 两相邻对称轴之间的距离为
两相邻对称轴之间的距离为 .
.
(1)求 的单调增区间;
的单调增区间;
(2)若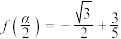 ,
, ,求
,求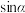 .
.
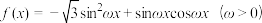 .若
.若 两相邻对称轴之间的距离为
两相邻对称轴之间的距离为 .
.(1)求
 的单调增区间;
的单调增区间;(2)若
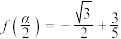 ,
, ,求
,求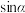 .
.
您最近一年使用:0次
7 . 已知向量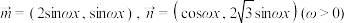 ,函数
,函数 的最小正周期为
的最小正周期为 ,
,
(1)求 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)求函数 在
在 上的值域.
上的值域.
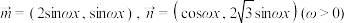 ,函数
,函数 的最小正周期为
的最小正周期为 ,
,(1)求
 的解析式和单调递增区间;
的解析式和单调递增区间;(2)求函数
 在
在 上的值域.
上的值域.
您最近一年使用:0次
8 . 已知函数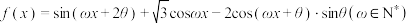 ,若函数
,若函数 在
在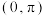 上恰好有两个零点.
上恰好有两个零点.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)当 时,关于
时,关于 的方程
的方程 有两个不同的实根,求实数
有两个不同的实根,求实数 的取值范围;
的取值范围;
(3)在 中,设内角
中,设内角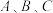 所对的边分别为
所对的边分别为 ,其中
,其中 ,
, 的角平分线交
的角平分线交 于
于 ,求线段
,求线段 的长度.
的长度.
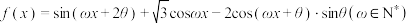 ,若函数
,若函数 在
在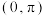 上恰好有两个零点.
上恰好有两个零点.(1)求函数
 的单调递增区间;
的单调递增区间;(2)当
 时,关于
时,关于 的方程
的方程 有两个不同的实根,求实数
有两个不同的实根,求实数 的取值范围;
的取值范围;(3)在
 中,设内角
中,设内角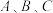 所对的边分别为
所对的边分别为 ,其中
,其中 ,
, 的角平分线交
的角平分线交 于
于 ,求线段
,求线段 的长度.
的长度.
您最近一年使用:0次
名校
9 . 已知函数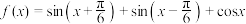 ,
,
(1)求 的单调递减区间;
的单调递减区间;
(2)在 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若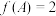 ,
, ,
,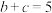 ,求
,求 的面积
的面积 .
.
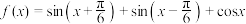 ,
,(1)求
 的单调递减区间;
的单调递减区间;(2)在
 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若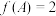 ,
, ,
,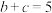 ,求
,求 的面积
的面积 .
.
您最近一年使用:0次
10 . 如图是函数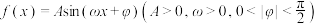 图象的一部分.
图象的一部分. 的解析式;
的解析式;
(2)求函数 的单调区间;
的单调区间;
(3)记方程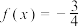 在
在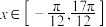 上的根从小到大依次为
上的根从小到大依次为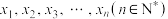 ,若
,若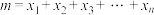 ,试求
,试求 与
与 的值.
的值.
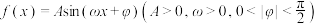 图象的一部分.
图象的一部分.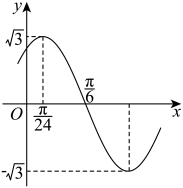
 的解析式;
的解析式;(2)求函数
 的单调区间;
的单调区间;(3)记方程
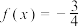 在
在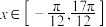 上的根从小到大依次为
上的根从小到大依次为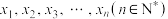 ,若
,若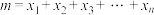 ,试求
,试求 与
与 的值.
的值.
您最近一年使用:0次
7日内更新
|
133次组卷
|
2卷引用:河北省张家口市2023-2024学年高一下学期期末考试数学试题



