2024高三·全国·专题练习
解题方法
1 . 已知锐角三角形 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,
, ,则
,则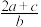 的取值范围是( )
的取值范围是( )
 的内角
的内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,
, ,则
,则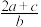 的取值范围是( )
的取值范围是( )A.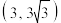 | B. | C.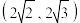 | D.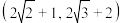 |
您最近半年使用:0次
名校
解题方法
2 . 在 中,角A、B、C的对边分别为a、b、c,已知
中,角A、B、C的对边分别为a、b、c,已知
(1)求角C的大小;
(2)若 ,求
,求 的周长的取值范围.
的周长的取值范围.
 中,角A、B、C的对边分别为a、b、c,已知
中,角A、B、C的对边分别为a、b、c,已知
(1)求角C的大小;
(2)若
 ,求
,求 的周长的取值范围.
的周长的取值范围.
您最近半年使用:0次
解题方法
3 . 在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足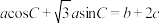 .则角
.则角
_______ .
 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足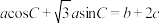 .则角
.则角
您最近半年使用:0次
名校
解题方法
4 . 在 中,角A,B,C的对边分别为a,b,c,S为
中,角A,B,C的对边分别为a,b,c,S为 的面积,且
的面积,且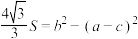 ,
, ,则
,则 的取值范围为( )
的取值范围为( )
 中,角A,B,C的对边分别为a,b,c,S为
中,角A,B,C的对边分别为a,b,c,S为 的面积,且
的面积,且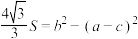 ,
, ,则
,则 的取值范围为( )
的取值范围为( )A.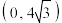 | B.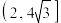 | C.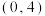 | D. |
您最近半年使用:0次
名校
解题方法
5 . 在锐角 中,已知角A,B,C所对的边分别为a,b,c,且
中,已知角A,B,C所对的边分别为a,b,c,且 .
.
(1)求角C的大小;
(2)求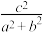 的取值范围.
的取值范围.
 中,已知角A,B,C所对的边分别为a,b,c,且
中,已知角A,B,C所对的边分别为a,b,c,且 .
.(1)求角C的大小;
(2)求
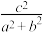 的取值范围.
的取值范围.
您最近半年使用:0次
名校
6 . 在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且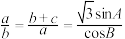 .
.
(1)求 .
.
(2)若 ,点
,点 是边
是边 上的两个动点,当
上的两个动点,当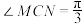 时,求
时,求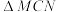 面积的取值范围.
面积的取值范围.
(3)若点 是直线
是直线 上的两个动点,记
上的两个动点,记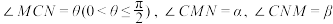 .若
.若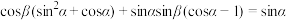 恒成立,求
恒成立,求 的值.
的值.
 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且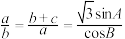 .
.(1)求
 .
.(2)若
 ,点
,点 是边
是边 上的两个动点,当
上的两个动点,当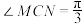 时,求
时,求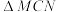 面积的取值范围.
面积的取值范围.(3)若点
 是直线
是直线 上的两个动点,记
上的两个动点,记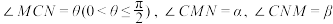 .若
.若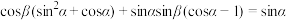 恒成立,求
恒成立,求 的值.
的值.
您最近半年使用:0次
解题方法
7 . 在 中,
中,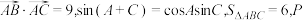 为线段
为线段 上的动点,且
上的动点,且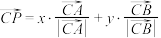 ,则
,则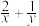 的最小值为( )
的最小值为( )
 中,
中,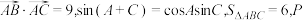 为线段
为线段 上的动点,且
上的动点,且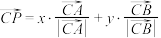 ,则
,则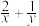 的最小值为( )
的最小值为( )A.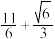 | B. | C.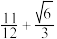 | D. |
您最近半年使用:0次
昨日更新
|
540次组卷
|
4卷引用:湖南省株洲市第十三中学2023-2024学年高一下学期3月月考数学试卷
湖南省株洲市第十三中学2023-2024学年高一下学期3月月考数学试卷(已下线)6.4.3.2?正弦定理15种常考题型归类(2)-高频考点通关与解题策略(人教A版2019必修第二册)浙江省嘉兴市第五高级中学2023-2024学年高一下学期4月月考数学试题(已下线)6.4.3.2 正弦定理——课堂例题
名校
解题方法
8 . 已知 的内角A,B,C所对的边分别为a,b,c,以下说法正确的是( )
的内角A,B,C所对的边分别为a,b,c,以下说法正确的是( )
 的内角A,B,C所对的边分别为a,b,c,以下说法正确的是( )
的内角A,B,C所对的边分别为a,b,c,以下说法正确的是( )A.若 , ,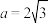 , , ,则 ,则 有两解 有两解 |
B.若 ,则 ,则 为等腰三角形 为等腰三角形 |
C.若 为锐角三角形,则 为锐角三角形,则 |
D.若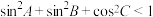 ,则 ,则 为钝角三角形 为钝角三角形 |
您最近半年使用:0次
名校
9 . 在 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .已知向量
.已知向量 ,
,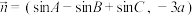 ,且
,且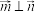 .
.
(1)求角 的大小;
的大小;
(2)若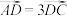 ,
,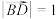 ,求
,求 的面积的最大值.
的面积的最大值.
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .已知向量
.已知向量 ,
,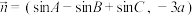 ,且
,且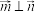 .
.(1)求角
 的大小;
的大小;(2)若
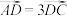 ,
,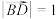 ,求
,求 的面积的最大值.
的面积的最大值.
您最近半年使用:0次
昨日更新
|
270次组卷
|
3卷引用:贵州省毕节市金沙县实验高级中学2023-2024学年高一下学期第一次月考数学试题
解题方法
10 . 在锐角 中,内角
中,内角 ,
, ,
, 所对边分别为
所对边分别为 ,
, ,
, ,
,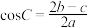 .
.
(1)求角 ;
;
(2)设 是角
是角 的平分线,与
的平分线,与 边交于
边交于 ,若
,若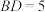 ,
,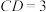 ,求
,求 ,
, ;
;
(3)若 ,求
,求 面积的取值范围.
面积的取值范围.
 中,内角
中,内角 ,
, ,
, 所对边分别为
所对边分别为 ,
, ,
, ,
,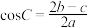 .
.(1)求角
 ;
;(2)设
 是角
是角 的平分线,与
的平分线,与 边交于
边交于 ,若
,若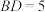 ,
,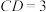 ,求
,求 ,
, ;
;(3)若
 ,求
,求 面积的取值范围.
面积的取值范围.
您最近半年使用:0次



