名校
解题方法
1 . 设 .
.
(1)若不等式 对一切实数x恒成立,求实数m的取值范围;
对一切实数x恒成立,求实数m的取值范围;
(2)在(1)的条件下,求 的最小值;
的最小值;
(3)解关于x的不等式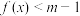 .
.
 .
.(1)若不等式
 对一切实数x恒成立,求实数m的取值范围;
对一切实数x恒成立,求实数m的取值范围;(2)在(1)的条件下,求
 的最小值;
的最小值;(3)解关于x的不等式
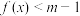 .
.
您最近半年使用:0次
名校
解题方法
2 . 若函数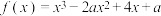 不存在极值,则
不存在极值,则 的取值范围是( )
的取值范围是( )
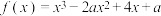 不存在极值,则
不存在极值,则 的取值范围是( )
的取值范围是( )A. | B.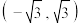 | C. | D.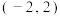 |
您最近半年使用:0次
7日内更新
|
1340次组卷
|
5卷引用:山东省大联考2023-2024学年高二下学期3月质量检测联合调考数学试题
山东省大联考2023-2024学年高二下学期3月质量检测联合调考数学试题(已下线)高二 模块3 专题2 小题进阶提升练广东省佛山市顺德区镇街联考2023-2024学年高二下学期4月月考数学试题(已下线)5.3.2.1函数的极值——课后作业(基础版)安徽省淮南第二中学2023-2024学年高二下学期期中教学检测数学试题
名校
解题方法
3 . 设m为给定的实常数,命题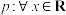 ,
, ,则“
,则“ ”是“p为真命题”的( )
”是“p为真命题”的( )
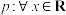 ,
, ,则“
,则“ ”是“p为真命题”的( )
”是“p为真命题”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
解题方法
4 . 已知不等式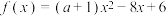 ,
, 的解集是
的解集是 .
.
(1)求常数 的值;
的值;
(2)若关于 的不等式
的不等式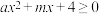 的解集为
的解集为 ,求
,求 的取值范围.
的取值范围.
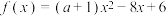 ,
, 的解集是
的解集是 .
.(1)求常数
 的值;
的值;(2)若关于
 的不等式
的不等式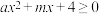 的解集为
的解集为 ,求
,求 的取值范围.
的取值范围.
您最近半年使用:0次
2024-04-18更新
|
223次组卷
|
2卷引用:湖南省株洲市第十三中学2023-2024学年高一下学期3月月考数学试卷
解题方法
5 . 下列说法正确的是( )
A.若函数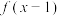 的定义域为 的定义域为 ,则函数 ,则函数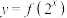 的定义域为 的定义域为 |
B.当 时,不等式 时,不等式 恒成立,则 恒成立,则 的取值范围是 的取值范围是 |
C.函数 在区间 在区间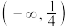 上单调递减 上单调递减 |
D.若函数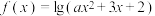 的值域为 的值域为 ,则实数 ,则实数 的取值范围是 的取值范围是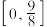 |
您最近半年使用:0次
名校
解题方法
6 . 命题“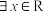 ,
, ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )
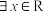 ,
, ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )A.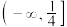 | B.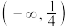 | C.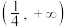 | D.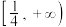 |
您最近半年使用:0次
名校
解题方法
7 . 已知条件 :“不等式
:“不等式 的解集是空集”,则条件
的解集是空集”,则条件 : “
: “ ”是条件
”是条件 的( )
的( )
 :“不等式
:“不等式 的解集是空集”,则条件
的解集是空集”,则条件 : “
: “ ”是条件
”是条件 的( )
的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
2024-04-13更新
|
552次组卷
|
2卷引用:山东省菏泽市第一中学南京路校区2024届高三下学期2月月考数学试题
解题方法
8 . 已知集合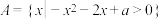 ,
, ,若
,若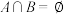 ,则
,则 的取值范围是
的取值范围是________ .
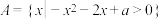 ,
, ,若
,若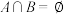 ,则
,则 的取值范围是
的取值范围是
您最近半年使用:0次
9 . 对于函数 ,若存在
,若存在 ,使得
,使得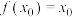 ,则称
,则称 是
是 的一个不动点.已知函数
的一个不动点.已知函数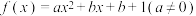 对于任意
对于任意 恒有两个相异的不动点,则实数
恒有两个相异的不动点,则实数 的取值范围是
的取值范围是______ .
 ,若存在
,若存在 ,使得
,使得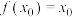 ,则称
,则称 是
是 的一个不动点.已知函数
的一个不动点.已知函数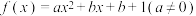 对于任意
对于任意 恒有两个相异的不动点,则实数
恒有两个相异的不动点,则实数 的取值范围是
的取值范围是
您最近半年使用:0次
名校
10 . 条件 是
是 的充分不必要条件是( )
的充分不必要条件是( )
 是
是 的充分不必要条件是( )
的充分不必要条件是( )A.函数 定义域为 定义域为 , , : : 在A上成立. 在A上成立. : : 为增函数; 为增函数; |
B. : : 成立, 成立, : :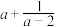 最小值为4; 最小值为4; |
C.p:函数 在区间 在区间 恰有一个零点,q: 恰有一个零点,q: 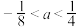 ; ; |
D.p:函数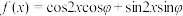 为偶函数( 为偶函数( ),q: ),q: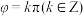 |
您最近半年使用:0次



