已知函数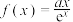 和
和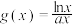 有相同的最大值
有相同的最大值 .
.
(1)求 ;
;
(2)证明:存在直线 ,其与两条曲线
,其与两条曲线 和
和 共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.
共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.
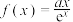 和
和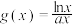 有相同的最大值
有相同的最大值 .
.(1)求
 ;
;(2)证明:存在直线
 ,其与两条曲线
,其与两条曲线 和
和 共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.
共有三个不同的交点,并且从左到右的三个交点的横坐标成等比数列.
22-23高三下·安徽池州·阶段练习 查看更多[3]
安徽省池州市贵池区池州市第一中学2022-2023学年高三4月月考数学试题(已下线)重难点突破11 导数中的同构问题(六大题型)(已下线)拔高点突破03 导数中的朗博同构、双元同构、指对同构与二次同构问题(九大题型)
更新时间:2023/05/11 16:36:45
|
相似题推荐
解答题-问答题
|
较难
(0.4)
【推荐1】设函数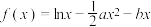 在点
在点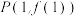 处的切线方程是
处的切线方程是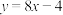
(1)求实数 的值.
的值.
(2)若方程 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.
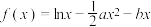 在点
在点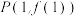 处的切线方程是
处的切线方程是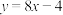
(1)求实数
 的值.
的值.(2)若方程
 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐2】已知函数 ,曲线
,曲线 在
在 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)函数 在区间
在区间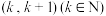 上存在零点,求
上存在零点,求 的值;
的值;
(3)记函数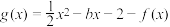 ,设
,设 (
( )是函数
)是函数 的两个极值点,若
的两个极值点,若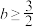 ,且
,且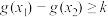 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
 ,曲线
,曲线 在
在 处的切线方程为
处的切线方程为 .
.(1)求
 的值;
的值;(2)函数
 在区间
在区间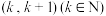 上存在零点,求
上存在零点,求 的值;
的值;(3)记函数
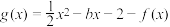 ,设
,设 (
( )是函数
)是函数 的两个极值点,若
的两个极值点,若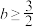 ,且
,且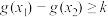 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐3】已知函数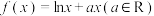 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若 ,且存在
,且存在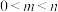 ,使得
,使得 在
在 上的值域
上的值域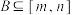 ,求实数a的取值范围.
,求实数a的取值范围.
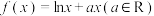 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
 ,且存在
,且存在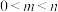 ,使得
,使得 在
在 上的值域
上的值域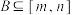 ,求实数a的取值范围.
,求实数a的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐1】(1)已知函数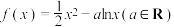 .若函数
.若函数 在
在 时取得极值,求实数
时取得极值,求实数 的值;
的值;
(2)已知函数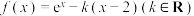 .试探求函数
.试探求函数 零点的个数,并证明你的结论.
零点的个数,并证明你的结论.
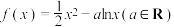 .若函数
.若函数 在
在 时取得极值,求实数
时取得极值,求实数 的值;
的值;(2)已知函数
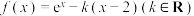 .试探求函数
.试探求函数 零点的个数,并证明你的结论.
零点的个数,并证明你的结论.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】已知 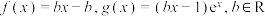 .
.
(1)若 ,讨论
,讨论 的单调性;
的单调性;
(2)若不等式 有且仅有两个整数解,求
有且仅有两个整数解,求 的取值范围.
的取值范围.
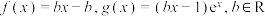 .
.(1)若
 ,讨论
,讨论 的单调性;
的单调性;(2)若不等式
 有且仅有两个整数解,求
有且仅有两个整数解,求 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐1】已知函数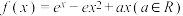 .
.
(1)若 在
在 上单调,求
上单调,求 的取值范围.
的取值范围.
(2)若 的图像恒在
的图像恒在 轴上方,求
轴上方,求 的取值范围.
的取值范围.
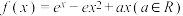 .
.(1)若
 在
在 上单调,求
上单调,求 的取值范围.
的取值范围.(2)若
 的图像恒在
的图像恒在 轴上方,求
轴上方,求 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】设函数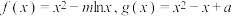 .
.
(1)当 时,
时, 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,若函数
时,若函数 在
在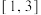 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围;
的取值范围;
(3)是否存在常数 ,使函数
,使函数 和函数
和函数 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
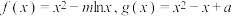 .
.(1)当
 时,
时, 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;(2)当
 时,若函数
时,若函数 在
在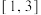 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围;
的取值范围;(3)是否存在常数
 ,使函数
,使函数 和函数
和函数 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐3】已知函数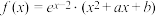 ,
, 的图象在点
的图象在点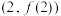 处的切线方程为
处的切线方程为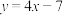 .
.
(1)求 在
在 上的最值.
上的最值.
(2)若 的解集为
的解集为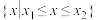 ,且在
,且在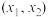 内有且只有两个整数,求实数
内有且只有两个整数,求实数 的取值范围.
的取值范围.
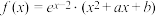 ,
, 的图象在点
的图象在点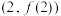 处的切线方程为
处的切线方程为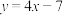 .
.(1)求
 在
在 上的最值.
上的最值.(2)若
 的解集为
的解集为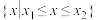 ,且在
,且在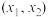 内有且只有两个整数,求实数
内有且只有两个整数,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】已知函数
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若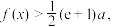 求实数
求实数 的取值范围(e是常数对数的底数且e=2.71828...).
的取值范围(e是常数对数的底数且e=2.71828...).

(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若
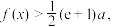 求实数
求实数 的取值范围(e是常数对数的底数且e=2.71828...).
的取值范围(e是常数对数的底数且e=2.71828...).
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若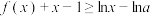 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
 .
.(1)讨论函数
 的单调性;
的单调性;(2)若
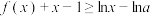 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐3】已知 .
.
(1)求函数 在区间
在区间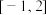 上的值域;
上的值域;
(2)当 时,
时,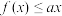 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)求函数
 在区间
在区间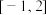 上的值域;
上的值域;(2)当
 时,
时,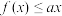 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次

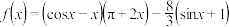 ,
,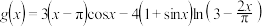 .证明:
.证明: 上单调递减,且存在唯一
上单调递减,且存在唯一 ,使得
,使得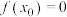 ;
;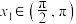 ,使得
,使得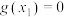 ,且对(1)中的
,且对(1)中的 有:
有: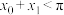 .
.


