解题方法
1 . 对集合 ,定义其特征函数
,定义其特征函数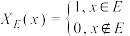 ,考虑集合
,考虑集合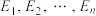 和正实数
和正实数 ,定义
,定义 为
为 和式函数.设
和式函数.设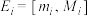 ,则
,则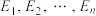 为闭区间列;如果集合
为闭区间列;如果集合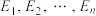 对任意
对任意 ,有
,有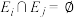 ,则称
,则称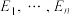 是无交集合列,设集合
是无交集合列,设集合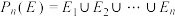 .
.
(1)证明:L和式函数的值域为有限集合;
(2)设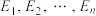 为闭区间列,
为闭区间列,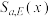 是定义在
是定义在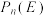 上的函数.已知存在唯一的正整数
上的函数.已知存在唯一的正整数 ,各项不同的非零实数
,各项不同的非零实数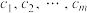 ,和无交集合列
,和无交集合列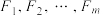 使得
使得 ,并且
,并且 ,称
,称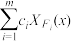 为
为 和式函数
和式函数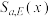 的典范形式.设
的典范形式.设 为
为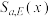 的典范数.
的典范数.
(i)设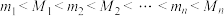 ,证明:
,证明: ;
;
(ii)给定正整数 ,任取正实数
,任取正实数 和闭区间列
和闭区间列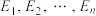 ,判断
,判断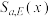 的典范数
的典范数 最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
 ,定义其特征函数
,定义其特征函数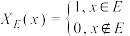 ,考虑集合
,考虑集合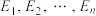 和正实数
和正实数 ,定义
,定义 为
为 和式函数.设
和式函数.设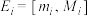 ,则
,则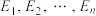 为闭区间列;如果集合
为闭区间列;如果集合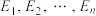 对任意
对任意 ,有
,有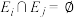 ,则称
,则称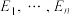 是无交集合列,设集合
是无交集合列,设集合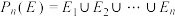 .
.(1)证明:L和式函数的值域为有限集合;
(2)设
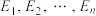 为闭区间列,
为闭区间列,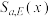 是定义在
是定义在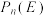 上的函数.已知存在唯一的正整数
上的函数.已知存在唯一的正整数 ,各项不同的非零实数
,各项不同的非零实数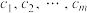 ,和无交集合列
,和无交集合列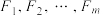 使得
使得 ,并且
,并且 ,称
,称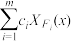 为
为 和式函数
和式函数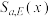 的典范形式.设
的典范形式.设 为
为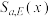 的典范数.
的典范数.(i)设
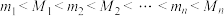 ,证明:
,证明: ;
;(ii)给定正整数
 ,任取正实数
,任取正实数 和闭区间列
和闭区间列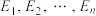 ,判断
,判断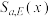 的典范数
的典范数 最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
最大值的存在性.如果存在,给出最大值;如果不存在,说明理由.
您最近一年使用:0次
2 . 对实数 ,不超过
,不超过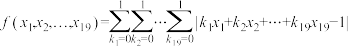 的最小值的最大整数为
的最小值的最大整数为__________ .
 ,不超过
,不超过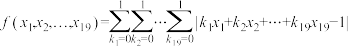 的最小值的最大整数为
的最小值的最大整数为
您最近一年使用:0次
3 . 已知集合 ,A是M的子集,当
,A是M的子集,当 时,
时, ,则集合A元素个数的最大值为
,则集合A元素个数的最大值为_______ .
 ,A是M的子集,当
,A是M的子集,当 时,
时, ,则集合A元素个数的最大值为
,则集合A元素个数的最大值为
您最近一年使用:0次
2021-09-16更新
|
861次组卷
|
3卷引用:全国高中数学联赛模拟试题(十五)
4 . 在复平面上,任取方程 的三个不同的根为顶点组成三角形,则不同的锐角三角形的数目为
的三个不同的根为顶点组成三角形,则不同的锐角三角形的数目为____________ .
 的三个不同的根为顶点组成三角形,则不同的锐角三角形的数目为
的三个不同的根为顶点组成三角形,则不同的锐角三角形的数目为
您最近一年使用:0次
5 . 设数列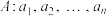 (
( )的各项均为正整数,且
)的各项均为正整数,且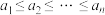 .若对任意
.若对任意 ,存在正整数
,存在正整数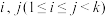 使得
使得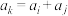 ,则称数列
,则称数列 具有性质
具有性质 .
.
(1)判断数列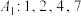 与数列
与数列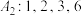 是否具有性质
是否具有性质 ;(只需写出结论)
;(只需写出结论)
(2)若数列 具有性质
具有性质 ,且
,且 ,
, ,
, ,求
,求 的最小值;
的最小值;
(3)若集合 ,且
,且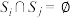 (任意
(任意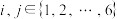 ,
,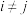 ).求证:存在
).求证:存在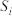 ,使得从
,使得从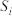 中可以选取若干元素(可重复选取)组成一个具有性质
中可以选取若干元素(可重复选取)组成一个具有性质 的数列.
的数列.
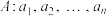 (
( )的各项均为正整数,且
)的各项均为正整数,且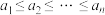 .若对任意
.若对任意 ,存在正整数
,存在正整数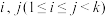 使得
使得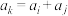 ,则称数列
,则称数列 具有性质
具有性质 .
.(1)判断数列
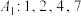 与数列
与数列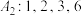 是否具有性质
是否具有性质 ;(只需写出结论)
;(只需写出结论)(2)若数列
 具有性质
具有性质 ,且
,且 ,
, ,
, ,求
,求 的最小值;
的最小值;(3)若集合
 ,且
,且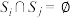 (任意
(任意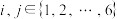 ,
,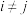 ).求证:存在
).求证:存在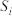 ,使得从
,使得从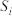 中可以选取若干元素(可重复选取)组成一个具有性质
中可以选取若干元素(可重复选取)组成一个具有性质 的数列.
的数列.
您最近一年使用:0次
2020-05-11更新
|
1306次组卷
|
8卷引用:2020届北京市朝阳区高三第一次模拟考试数学试题
2020届北京市朝阳区高三第一次模拟考试数学试题上海市2022届高三上学期一模暨春考模拟卷(四)数学试题北京师范大学第二附属中学2022届高三三模数学试题(已下线)北京市海淀区2023届高三上学期期末练习数学试题变式题16-21北京市2023届高三数学模拟试题北京卷专题18数列(解答题)北京市顺义区第一中学2023届高三高考考前适应性检测数学试题(已下线)数列的综合应用
6 . 设数组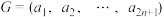 ,
, ,
,
 ,数
,数 称为数组
称为数组 的元素.对于数组
的元素.对于数组 ,规定:
,规定:
①数组 中所有元素的和为
中所有元素的和为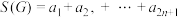 ;
;
②变换 ,
, 将数组
将数组 变换成数组
变换成数组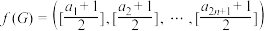 ,其中
,其中 表示不超过
表示不超过 的最大整数;
的最大整数;
③若数组 ,则当且仅当
,则当且仅当
 时,
时, .
.
如果对数组 中任意
中任意 个元素,存在一种分法,可将其分为两组,每组
个元素,存在一种分法,可将其分为两组,每组 个元素,使得两组所有元素的和相等,则称数组
个元素,使得两组所有元素的和相等,则称数组 具有性质
具有性质 .
.
(Ⅰ)已知数组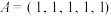 ,
,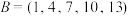 ,计算
,计算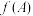 ,
, ,并写出数组
,并写出数组 是否具有性质
是否具有性质 ;
;
(Ⅱ)已知数组 具有性质
具有性质 ,证明:
,证明: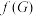 也具有性质
也具有性质 ;
;
(Ⅲ)证明:数组 具有性质
具有性质 的充要条件是
的充要条件是 .
.
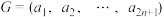 ,
, ,
,
 ,数
,数 称为数组
称为数组 的元素.对于数组
的元素.对于数组 ,规定:
,规定:①数组
 中所有元素的和为
中所有元素的和为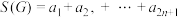 ;
;②变换
 ,
, 将数组
将数组 变换成数组
变换成数组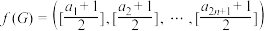 ,其中
,其中 表示不超过
表示不超过 的最大整数;
的最大整数;③若数组
 ,则当且仅当
,则当且仅当
 时,
时, .
.如果对数组
 中任意
中任意 个元素,存在一种分法,可将其分为两组,每组
个元素,存在一种分法,可将其分为两组,每组 个元素,使得两组所有元素的和相等,则称数组
个元素,使得两组所有元素的和相等,则称数组 具有性质
具有性质 .
.(Ⅰ)已知数组
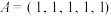 ,
,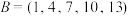 ,计算
,计算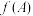 ,
, ,并写出数组
,并写出数组 是否具有性质
是否具有性质 ;
;(Ⅱ)已知数组
 具有性质
具有性质 ,证明:
,证明: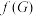 也具有性质
也具有性质 ;
;(Ⅲ)证明:数组
 具有性质
具有性质 的充要条件是
的充要条件是 .
.
您最近一年使用:0次
7 . 考查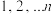 所有排列,将每种排列视为一个
所有排列,将每种排列视为一个 元有序实数组
元有序实数组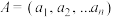 ,设
,设 且
且 ,设
,设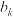 为
为 的最大项,其中
的最大项,其中 .记数组
.记数组 为
为 .例如,
.例如,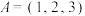 时,
时,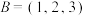 ;
;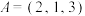 时,
时,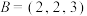 .若数组
.若数组 中的不同元素个数为2.
中的不同元素个数为2.
(1)若 ,求所有
,求所有 元有序实数组
元有序实数组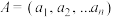 的个数;
的个数;
(2)求所有 元有序实数组
元有序实数组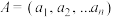 的个数.
的个数.
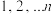 所有排列,将每种排列视为一个
所有排列,将每种排列视为一个 元有序实数组
元有序实数组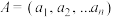 ,设
,设 且
且 ,设
,设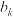 为
为 的最大项,其中
的最大项,其中 .记数组
.记数组 为
为 .例如,
.例如,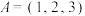 时,
时,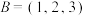 ;
;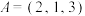 时,
时,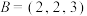 .若数组
.若数组 中的不同元素个数为2.
中的不同元素个数为2.(1)若
 ,求所有
,求所有 元有序实数组
元有序实数组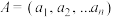 的个数;
的个数;(2)求所有
 元有序实数组
元有序实数组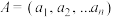 的个数.
的个数.
您最近一年使用:0次
名校
8 . 有限个元素组成的集合为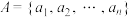 ,
, ,集合
,集合 中的元素个数记为
中的元素个数记为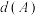 ,定义
,定义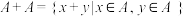 ,集合
,集合 的个数记为
的个数记为 ,当
,当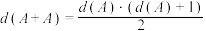 ,称集合
,称集合 具有性质
具有性质 .
.
(1)设集合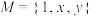 具有性质
具有性质 ,判断集合
,判断集合 中的三个元素是否能组成等差数列,请说明理由;
中的三个元素是否能组成等差数列,请说明理由;
(2) 设正数列 的前
的前 项和为
项和为 ,满足
,满足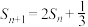 ,其中
,其中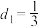 ,数列
,数列 中的前
中的前 项:
项: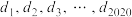 组成的集合
组成的集合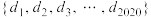 记作
记作 ,将集合
,将集合 中的所有元素
中的所有元素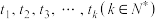 从小到大排序,即
从小到大排序,即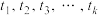 满足
满足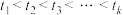 ,求
,求 ;
;
(3) 已知集合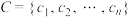 ,其中数列
,其中数列 是等比数列,
是等比数列, ,且公比是有理数,判断集合
,且公比是有理数,判断集合 是否具有性质
是否具有性质 ,说明理由.
,说明理由.
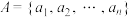 ,
, ,集合
,集合 中的元素个数记为
中的元素个数记为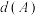 ,定义
,定义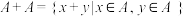 ,集合
,集合 的个数记为
的个数记为 ,当
,当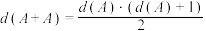 ,称集合
,称集合 具有性质
具有性质 .
.(1)设集合
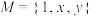 具有性质
具有性质 ,判断集合
,判断集合 中的三个元素是否能组成等差数列,请说明理由;
中的三个元素是否能组成等差数列,请说明理由;(2) 设正数列
 的前
的前 项和为
项和为 ,满足
,满足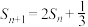 ,其中
,其中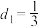 ,数列
,数列 中的前
中的前 项:
项: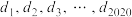 组成的集合
组成的集合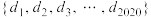 记作
记作 ,将集合
,将集合 中的所有元素
中的所有元素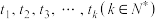 从小到大排序,即
从小到大排序,即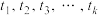 满足
满足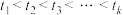 ,求
,求 ;
;(3) 已知集合
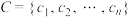 ,其中数列
,其中数列 是等比数列,
是等比数列, ,且公比是有理数,判断集合
,且公比是有理数,判断集合 是否具有性质
是否具有性质 ,说明理由.
,说明理由.
您最近一年使用:0次
2020-01-13更新
|
754次组卷
|
3卷引用:上海市奉贤区2019-2020学年高三上学期第一次模拟考试(期末)数学试题



