名校
解题方法
1 . 已知抛物线 的顶点是椭圆
的顶点是椭圆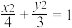 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.
(1)求抛物线 的方程;
的方程;
(2)已知动直线 过点
过点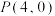 ,交抛物线
,交抛物线 于
于 、
、 两点,坐标原点
两点,坐标原点 为
为 中点,
中点,
①求证: ;
;
②是否存在垂直于 轴的直线
轴的直线 被以
被以 为直径的圆所截得的弦长恒为定值?如果存在,求出
为直径的圆所截得的弦长恒为定值?如果存在,求出 的方程;如果不存在,说明理由.
的方程;如果不存在,说明理由.
 的顶点是椭圆
的顶点是椭圆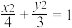 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.(1)求抛物线
 的方程;
的方程;(2)已知动直线
 过点
过点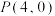 ,交抛物线
,交抛物线 于
于 、
、 两点,坐标原点
两点,坐标原点 为
为 中点,
中点,①求证:
 ;
;②是否存在垂直于
 轴的直线
轴的直线 被以
被以 为直径的圆所截得的弦长恒为定值?如果存在,求出
为直径的圆所截得的弦长恒为定值?如果存在,求出 的方程;如果不存在,说明理由.
的方程;如果不存在,说明理由.
您最近一年使用:0次
2024-06-03更新
|
425次组卷
|
9卷引用:2020年浙江省名校高考仿真训练卷(四)
2020年浙江省名校高考仿真训练卷(四)浙江省金华一中2018届高三下学期5月高考模拟考试数学试题河北省秦皇岛市新世纪高级中学2023-2024学年高二下学期开学考试数学试卷上海市2022届高三上学期一模暨春考模拟卷(四)数学试题上海市2022届高三上学期一模暨春考模拟卷(三)数学试题黑龙江省哈尔滨市第九中学校2023-2024学年高二下学期期中考试数学学科试卷(已下线)专题4 抛物线切线与阿基米德三角形【练】(压轴题大全)(已下线)重难点突破15 圆锥曲线中的经典七大名圆问题(七大题型)(已下线)重组8 高二期中真题重组卷(辽宁卷)B提升卷
名校
解题方法
2 . 设椭圆 的左,右焦点分别为
的左,右焦点分别为 ,其离心率为
,其离心率为 ,且点
,且点 在C上.
在C上.
(1)求C的方程;
(2)O为坐标原点,P为C上任意一点.若M为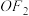 的中点,过M且平行于
的中点,过M且平行于 的直线l交椭圆C于A,B两点,是否存在实数
的直线l交椭圆C于A,B两点,是否存在实数 ,使得
,使得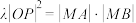 ?若存在,求
?若存在,求 值;若不存在,说明理由.
值;若不存在,说明理由.
 的左,右焦点分别为
的左,右焦点分别为 ,其离心率为
,其离心率为 ,且点
,且点 在C上.
在C上.(1)求C的方程;
(2)O为坐标原点,P为C上任意一点.若M为
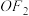 的中点,过M且平行于
的中点,过M且平行于 的直线l交椭圆C于A,B两点,是否存在实数
的直线l交椭圆C于A,B两点,是否存在实数 ,使得
,使得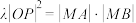 ?若存在,求
?若存在,求 值;若不存在,说明理由.
值;若不存在,说明理由.
您最近一年使用:0次
2022-02-21更新
|
854次组卷
|
18卷引用:河北省秦皇岛市抚宁区第一中学2019-2020学年高二上学期期末数学试题
河北省秦皇岛市抚宁区第一中学2019-2020学年高二上学期期末数学试题贵州省贵阳市第一中学2020届高三上学期第三次月考数学(文)试题宁夏石嘴山市第三中学2019-2020学年高二上学期期末考试数学(理)试题河北省唐山市2019-2020学年高二上学期期末数学试题2020届江西省赣州市赣县三中高三1月考前适应性考试数学(理)试题海南省海南枫叶国际学校2019-2020学年高二上学期期末考试数学试题(已下线)专题05 圆锥曲线中的证明问题、探究性问题(第五篇)-2020高考数学压轴题命题区间探究与突破四川省宜宾市叙州区第二中学校2020届高三第一次高考适应性考试数学(理)试题四川省宜宾市叙州区第二中学校2020届高三第一次高考适应性考试数学(文)试题(已下线)专题19 圆锥曲线综合-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)专题19 圆锥曲线综合-2020年高考数学(文)母题题源解密(全国Ⅱ专版)西藏山南市第二高级中学2020届高三第三次模拟考试数学(文)试题西藏山南市第二高级中学2020届高三第三次模拟考试数学(理)试题广西桂林市2021-2022学年高二上学期期末考试数学(理)试题(已下线)解密18 椭圆 (讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(全国通用)(已下线)专题29 弦长问题及长度和、差、商、积问题-2第三章 圆锥曲线的方程单元测试(基础版)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)江西省南昌市铁路第一中学2022-2023学年高二下学期3月月考数学试题
解题方法
3 . 已知数列 的前
的前 项和为
项和为 ,
, ,
, ,数列
,数列 满足
满足 ,
, ,对任意
,对任意 ,都有
,都有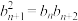 .
.
(1)求数列 、
、 的通项公式.
的通项公式.
(2)令 ,若对任意的
,若对任意的 ,不等式
,不等式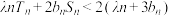 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
 的前
的前 项和为
项和为 ,
, ,
, ,数列
,数列 满足
满足 ,
, ,对任意
,对任意 ,都有
,都有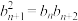 .
.(1)求数列
 、
、 的通项公式.
的通项公式.(2)令
 ,若对任意的
,若对任意的 ,不等式
,不等式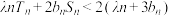 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 已知抛物线 :
:
 上一点
上一点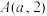 到焦点的距离为2.
到焦点的距离为2.
(1)求抛物线 的标准方程;
的标准方程;
(2)若在 轴上存在点
轴上存在点 ,过点
,过点 的直线
的直线 分别与抛物线
分别与抛物线 相交于
相交于 、
、 两点,若
两点,若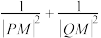 为定值,求点
为定值,求点 的坐标及此定值.
的坐标及此定值.
 :
:
 上一点
上一点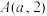 到焦点的距离为2.
到焦点的距离为2.(1)求抛物线
 的标准方程;
的标准方程; (2)若在
 轴上存在点
轴上存在点 ,过点
,过点 的直线
的直线 分别与抛物线
分别与抛物线 相交于
相交于 、
、 两点,若
两点,若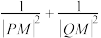 为定值,求点
为定值,求点 的坐标及此定值.
的坐标及此定值.
您最近一年使用:0次
解题方法
5 . 对于函数 ,
, ,如果存在实数s,使得
,如果存在实数s,使得 ,
, 同时成立,则称函数
同时成立,则称函数 和
和 互为“亲密函数”.若函数
互为“亲密函数”.若函数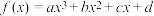 ,
,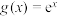 (其中a,b,c,d为实数,e为自然对数的底数).
(其中a,b,c,d为实数,e为自然对数的底数).
(1)当 ,
,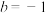 ,
, 时,判断函数
时,判断函数 和
和 是否互为“亲密函数”,并说明理由;
是否互为“亲密函数”,并说明理由;
(2)当 时,若函数
时,若函数 和
和 互为“亲密函数”,求证:对任意的实数x都满足
互为“亲密函数”,求证:对任意的实数x都满足 .
.
 ,
, ,如果存在实数s,使得
,如果存在实数s,使得 ,
, 同时成立,则称函数
同时成立,则称函数 和
和 互为“亲密函数”.若函数
互为“亲密函数”.若函数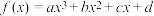 ,
,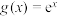 (其中a,b,c,d为实数,e为自然对数的底数).
(其中a,b,c,d为实数,e为自然对数的底数).(1)当
 ,
,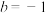 ,
, 时,判断函数
时,判断函数 和
和 是否互为“亲密函数”,并说明理由;
是否互为“亲密函数”,并说明理由;(2)当
 时,若函数
时,若函数 和
和 互为“亲密函数”,求证:对任意的实数x都满足
互为“亲密函数”,求证:对任意的实数x都满足 .
.
您最近一年使用:0次
2020-07-24更新
|
162次组卷
|
2卷引用:江苏省苏州市2019-2020学年高二下学期期末数学试题
6 . 已知函数 ,对任意
,对任意 ,都有
,都有 .
.
(1)求实数m的取值范围;
(2)若当 时,
时,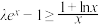 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,对任意
,对任意 ,都有
,都有 .
.(1)求实数m的取值范围;
(2)若当
 时,
时,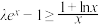 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-07-04更新
|
238次组卷
|
2卷引用:湖北省武汉市武昌区2020届高三下学期六月供题文科数学试题
名校
7 . 设函数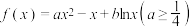
(1)若 是函数
是函数 的一个极值点,求函数
的一个极值点,求函数 的单调区间;
的单调区间;
(2)当 时,对于任意的
时,对于任意的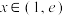 (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
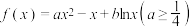
(1)若
 是函数
是函数 的一个极值点,求函数
的一个极值点,求函数 的单调区间;
的单调区间;(2)当
 时,对于任意的
时,对于任意的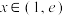 (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-04-15更新
|
215次组卷
|
2卷引用:河北省秦皇岛市抚宁区第一中学2019-2020学年高二下学期3月阶段性考试数学(理)试题
8 . 已知函数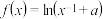 .
.
(1)设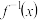 是
是 的反函数.当
的反函数.当 时,解不等式
时,解不等式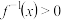 ;
;
(2)若关于 的方程
的方程 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数 的值;
的值;
(3)设 ,若对任意
,若对任意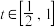 ,函数
,函数 在区间
在区间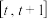 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过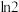 ,求
,求 的取值范围.
的取值范围.
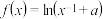 .
.(1)设
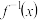 是
是 的反函数.当
的反函数.当 时,解不等式
时,解不等式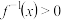 ;
;(2)若关于
 的方程
的方程 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数 的值;
的值;(3)设
 ,若对任意
,若对任意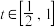 ,函数
,函数 在区间
在区间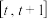 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过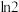 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2020-02-01更新
|
284次组卷
|
2卷引用:上海市杨浦区2018届高三上学期期中数学试题
名校
9 . 已知:椭圆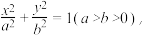 过点
过点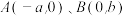 直线倾斜角为
直线倾斜角为 原点到该直线的距离为
原点到该直线的距离为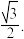
(1)求椭圆的方程;
(2)斜率大于零的直线过D(-1,0)与椭圆交于E、F两点,若 求直线EF的方程;
求直线EF的方程;
(3)是否存在实数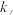 直线
直线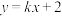 交椭圆于P、Q两点,以PQ为直径的圆过点D(-1,0)?若存在,求出
交椭圆于P、Q两点,以PQ为直径的圆过点D(-1,0)?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
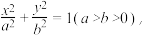 过点
过点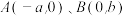 直线倾斜角为
直线倾斜角为 原点到该直线的距离为
原点到该直线的距离为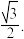
(1)求椭圆的方程;
(2)斜率大于零的直线过D(-1,0)与椭圆交于E、F两点,若
 求直线EF的方程;
求直线EF的方程;(3)是否存在实数
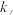 直线
直线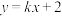 交椭圆于P、Q两点,以PQ为直径的圆过点D(-1,0)?若存在,求出
交椭圆于P、Q两点,以PQ为直径的圆过点D(-1,0)?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2019-11-10更新
|
579次组卷
|
2卷引用:上海市吴淞中学2018-2019学年高二上学期期末数学试题
名校
10 . 定义在非零实数集上的函数 对任意非零实数
对任意非零实数 满足:
满足: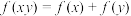 ,且当
,且当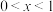 时
时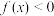 .
.
(1)求 及
及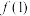 的值;
的值;
(2)求证: 是偶函数;
是偶函数;
(3)解不等式: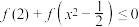 .
.
 对任意非零实数
对任意非零实数 满足:
满足: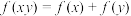 ,且当
,且当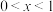 时
时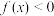 .
.(1)求
 及
及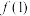 的值;
的值;(2)求证:
 是偶函数;
是偶函数;(3)解不等式:
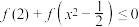 .
.
您最近一年使用:0次
2019-10-23更新
|
1117次组卷
|
5卷引用:贵州省遵义市凤冈县第一中学2019-2020学年高一上学期第一次月考数学试题



