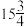1 . 在等差数列 中,填写下表:
中,填写下表:
思考填表过程,你能得出什么结论?
 中,填写下表:
中,填写下表:题号 |
|
|
|
|
(1) | 8 |
|
| |
(2) | 2 | 9 | 18 | |
(3) |
| 30 |
| |
(4) | 3 | 2 | 21 |
您最近一年使用:0次
2023-10-10更新
|
154次组卷
|
2卷引用:北师大版(2019)选择性必修第二册课本例题2.1 等差数列的概念及其通项公式
解题方法
2 . 作为上海市副中心之一,徐汇区的建设不仅是上海市发展战略的关键节点,也肩负着医治上海市“大城市病”的历史重任,因此,徐汇区的发展备受瞩目.2017年发布的《上海市徐汇区统计年鉴(2017)》显示:2016年徐汇区全区完成全社会固定资产投资939.9亿元,比上年增长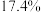 ,下面给出的是徐汇区2011~2016年全社会固定资产投资及增长率,如图一.又根据徐汇区统计局2018年1月25日发布:2017年徐汇区全区完成全社会固定资产投资1054.5亿元,比上年增长
,下面给出的是徐汇区2011~2016年全社会固定资产投资及增长率,如图一.又根据徐汇区统计局2018年1月25日发布:2017年徐汇区全区完成全社会固定资产投资1054.5亿元,比上年增长 .
.
(2)通过计算2011~2017这7年的平均增长率约为 ,现从2011~2017这7年中随机选取2个年份,记X为“选取的2个年份中,增长率高于
,现从2011~2017这7年中随机选取2个年份,记X为“选取的2个年份中,增长率高于 的年份的个数”,求X的分布列及数学期望.
的年份的个数”,求X的分布列及数学期望.
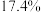 ,下面给出的是徐汇区2011~2016年全社会固定资产投资及增长率,如图一.又根据徐汇区统计局2018年1月25日发布:2017年徐汇区全区完成全社会固定资产投资1054.5亿元,比上年增长
,下面给出的是徐汇区2011~2016年全社会固定资产投资及增长率,如图一.又根据徐汇区统计局2018年1月25日发布:2017年徐汇区全区完成全社会固定资产投资1054.5亿元,比上年增长 .
.
(2)通过计算2011~2017这7年的平均增长率约为
 ,现从2011~2017这7年中随机选取2个年份,记X为“选取的2个年份中,增长率高于
,现从2011~2017这7年中随机选取2个年份,记X为“选取的2个年份中,增长率高于 的年份的个数”,求X的分布列及数学期望.
的年份的个数”,求X的分布列及数学期望.
您最近一年使用:0次
2023·浙江宁波·模拟预测
名校
3 . 浙江省是第一批新高考改革省份,取消文理分科,变成必考科目和选考科目.其中必考科目是语文、数学、外语,选考科目由考生在思想政治、历史、地理、物理、化学、生物、技术7个科目中自主选择其中3个科目参加等级性考试.为了调查学生对物理、化学、生物的选考情况,从镇海中学高三在物理、化学、生物三个科目中至少选考一科的学生中随机抽取100名学生进行调查,他们选考物理、化学、生物的科目数及人数统计如表:
(1)从这100名学生中任选2名,求他们选考物理、化学、生物科目数相等的概率;
(2)从这100名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数之差的绝对值,求随机变量X的数学期望;
(3)学校还调查了这100位学生的性别情况,研究男女生中纯理科生大概的比例,得到的数据如下表:(定文同时选考物理、化学、生物三科的学生为纯理科生)
请补齐表格,并说明依据小概率值 的独立性检验,能否认为同时选考物理、化学、生物三科与学生性别有关.
的独立性检验,能否认为同时选考物理、化学、生物三科与学生性别有关.
参考公式: ,其中
,其中 .
.
附表:
选考物理、化学、生物的科目数 | 1 | 2 | 3 |
人数 | 20 | 40 | 40 |
(2)从这100名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数之差的绝对值,求随机变量X的数学期望;
(3)学校还调查了这100位学生的性别情况,研究男女生中纯理科生大概的比例,得到的数据如下表:(定文同时选考物理、化学、生物三科的学生为纯理科生)
性别 | 纯理科生 | 非纯理科生 | 总计 |
男性 | 30 | ||
女性 | 5 | ||
总计 | 100 |
 的独立性检验,能否认为同时选考物理、化学、生物三科与学生性别有关.
的独立性检验,能否认为同时选考物理、化学、生物三科与学生性别有关.参考公式:
 ,其中
,其中 .
.附表:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
22-23高二上·上海浦东新·期中
名校
4 . 下列各图符合立体几何作图规范要求的是( )

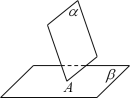
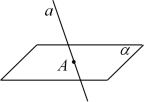

| A.直线在平面内 | B.平面与平面相交 | C.直线与平面相交 | D.两直线异面 |
您最近一年使用:0次
2022-11-25更新
|
728次组卷
|
9卷引用:专题01平面及其基本性质(9个知识点6种考法)(3)
(已下线)专题01平面及其基本性质(9个知识点6种考法)(3)上海市建平中学2022-2023学年高二上学期期中数学试题(已下线)期中真题必刷基础60题(21个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)第06讲 8.4.1 平面-【帮课堂】(人教A版2019必修第二册)(已下线)专题16 平面-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)专题17 平面的基本性质-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)8.4. 空间点、直线、平面之间的位置关系-同步题型分类归纳讲与练(人教A版2019必修第二册)(已下线)11.2平面的基本事实与推论-同步精品课堂(人教B版2019必修第四册)(已下线)11.1.2 构成空间几何体的基本元素-【帮课堂】(人教B版2019必修第四册)
2024高三·全国·专题练习
5 . 图中的树形图形为:第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该线段成135°角的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段.重复前面的作法作图至第n层.设树的第n层的最高点至水平线的距离为n层的树形的高度.试求:
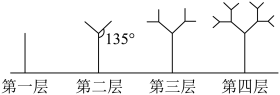
(1)第三层及第四层的树形图的高度
(2)第n层的树形图的高度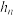
(3)若树形图的高度大于2,则称树形图为“高大”否则则称“矮小”.试判断该树形图是“高大”还是“矮小”的?

(1)第三层及第四层的树形图的高度
(2)第n层的树形图的高度
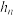
(3)若树形图的高度大于2,则称树形图为“高大”否则则称“矮小”.试判断该树形图是“高大”还是“矮小”的?
您最近一年使用:0次
6 . 如图,正方形 的边长为2cm,取正方形
的边长为2cm,取正方形 各边的中点E,F,G,H,作第二个正方形
各边的中点E,F,G,H,作第二个正方形 ,然后再取正方形
,然后再取正方形 各边的中点I,J,K,L,作第三个正方形,依此方法一直继续下去,如果这个作图过程可以一直继续下去,当操作次数无限增大时,所有这些正方形的面积之和将无限趋近于常数
各边的中点I,J,K,L,作第三个正方形,依此方法一直继续下去,如果这个作图过程可以一直继续下去,当操作次数无限增大时,所有这些正方形的面积之和将无限趋近于常数_______________ .
 的边长为2cm,取正方形
的边长为2cm,取正方形 各边的中点E,F,G,H,作第二个正方形
各边的中点E,F,G,H,作第二个正方形 ,然后再取正方形
,然后再取正方形 各边的中点I,J,K,L,作第三个正方形,依此方法一直继续下去,如果这个作图过程可以一直继续下去,当操作次数无限增大时,所有这些正方形的面积之和将无限趋近于常数
各边的中点I,J,K,L,作第三个正方形,依此方法一直继续下去,如果这个作图过程可以一直继续下去,当操作次数无限增大时,所有这些正方形的面积之和将无限趋近于常数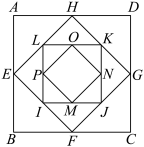
您最近一年使用:0次
22-23高二上·上海宝山·期中
名校
7 . 已知正三棱柱 的底面边长为3cm,高为3cm,M、N、P分别是
的底面边长为3cm,高为3cm,M、N、P分别是 、
、 、
、 的中点.
的中点.
(1)用“斜二测”画法,作出此正三棱柱的直观图(严格按照直尺刻度);
(2)在(1)中作出过M、N、P三点的正三棱柱的截面(保留作图痕迹).
 的底面边长为3cm,高为3cm,M、N、P分别是
的底面边长为3cm,高为3cm,M、N、P分别是 、
、 、
、 的中点.
的中点.(1)用“斜二测”画法,作出此正三棱柱的直观图(严格按照直尺刻度);
(2)在(1)中作出过M、N、P三点的正三棱柱的截面(保留作图痕迹).
您最近一年使用:0次
2022-11-17更新
|
744次组卷
|
10卷引用:专题01平面及其基本性质(9个知识点6种考法)(3)
(已下线)专题01平面及其基本性质(9个知识点6种考法)(3)上海交通大学附属中学2022-2023学年高二上学期期中数学试题上海市向明中学2021-2022学年高二上学期期中数学试题(已下线)第11章 简单几何体(易错必刷30题6种题型专项训练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)期中真题必刷易错40题(17个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)模块一 专题5 基本立体图形和直观图 讲(已下线)第八章 立体几何初步(二)(知识归纳+题型突破)(1)-单元速记·巧练(人教A版2019必修第二册)(已下线)8.2立体图形的直观图--课后作业(提升版)(已下线)重难点专题09 立体几何中的截面问题-【帮课堂】(苏教版2019必修第二册)(已下线)第25讲 平面的交线截面问题
23-24高三下·四川绵阳·阶段练习
名校
8 . 乒乓球,被称为中国的“国球”.某中学对学生参加乒乓球运动的情况进行调查,将每周参加乒乓球运动超过2小时的学生称为“乒乓球爱好者”,否则称为“非乒乓球爱好者”,从调查结果中随机抽取100份进行分析,得到数据如表所示:
(1)补全 列联表,并判断我们能否有
列联表,并判断我们能否有 的把握认为是否为“乒乓球爱好者”与性别有关?
的把握认为是否为“乒乓球爱好者”与性别有关?
(2)为了解学生的乒乓球运动水平,现从抽取的“乒乓球爱好者”学生中按性别采用分层抽样的方法抽取3人,与体育老师进行乒乓球比赛,其中男乒乓球爱好者获胜的概率为 ,女乒乓球爱好者获胜的概率为
,女乒乓球爱好者获胜的概率为 ,每次比赛结果相互独立,记这3人获胜的人数为
,每次比赛结果相互独立,记这3人获胜的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式: .
.
乒乓球爱好者 | 非乒乓球爱好者 | 总计 | |
男 | 40 | 56 | |
女 | 24 | ||
总计 | 100 |
 列联表,并判断我们能否有
列联表,并判断我们能否有 的把握认为是否为“乒乓球爱好者”与性别有关?
的把握认为是否为“乒乓球爱好者”与性别有关?(2)为了解学生的乒乓球运动水平,现从抽取的“乒乓球爱好者”学生中按性别采用分层抽样的方法抽取3人,与体育老师进行乒乓球比赛,其中男乒乓球爱好者获胜的概率为
 ,女乒乓球爱好者获胜的概率为
,女乒乓球爱好者获胜的概率为 ,每次比赛结果相互独立,记这3人获胜的人数为
,每次比赛结果相互独立,记这3人获胜的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
| 0.05 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
 .
.
您最近一年使用:0次
2024-04-10更新
|
932次组卷
|
5卷引用:8.3.1分类变量与列联表+8.3.2独立性检验 第三练 能力提升拔高
(已下线)8.3.1分类变量与列联表+8.3.2独立性检验 第三练 能力提升拔高(已下线)第八章 成对数据的统计分析总结 第一课归纳本章考点辽宁省大连市第八中学2023-2024学年高二下学期期中考试数学试题四川省绵阳市三台中学校2024届高三下学期第三学月(4月)月考理科数学试题四川省成都市石室阳安学校2023-2024学年高三下学期4月月考数学(理)试题
2024·全国·模拟预测
解题方法
9 . 杭州第19届亚运会又称“2022年杭州亚运会”,是继1990年北京亚运会、2010年广州亚运会之后,中国第三次举办亚洲最高规格的国际综合性体育赛事.某高校部分学生十分关注杭州亚运会,若将累计关注杭州亚运会赛事消息50次及以上的学生称为“亚运会达人”,未达到50次的学生称为“非亚运会达人”.现从该校随机抽取100名学生,得到数据如表所示:
(1)补全 列联表,并判断能否有99%的把握认为是否为“亚运会达人”与性别有关?
列联表,并判断能否有99%的把握认为是否为“亚运会达人”与性别有关?
(2)现从样本的“亚运会达人”中按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取3人,记这3人中女生的人数为X,求X的分布列和数学期望.
附: ,
, .
.
| 亚运会达人 | 非亚运会达人 | 合计 | |
| 男生 | 40 | 56 | |
| 女生 | 24 | ||
| 合计 |
 列联表,并判断能否有99%的把握认为是否为“亚运会达人”与性别有关?
列联表,并判断能否有99%的把握认为是否为“亚运会达人”与性别有关?(2)现从样本的“亚运会达人”中按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取3人,记这3人中女生的人数为X,求X的分布列和数学期望.
附:
 ,
, .
. | 0.050 | 0.010 | 0.005 |
| k | 3.841 | 6.635 | 7.879 |
您最近一年使用:0次
10 . 乒乓球,被称为中国的“国球”,是一项集力量、速度、柔韧、灵敏和耐力素质为一体的球类运动,同时又是技术和战术完美结合的典型.打乒乓球能使眼球内部不断运动,血液循环增强,眼神经机能提高,因而能使眼睛疲劳消除或减轻,起到预防治疗近视的作用.乒乓球的球体小,速度快,攻防转换迅速,技术打法丰富多样,既要考虑技术的发挥,又要考虑战术的运用.乒乓球运动中要求大脑快速紧张地思考,这样可以促进大脑的血液循环,供给大脑充分的能量,具有很好的健脑功能.乒乓球运动中既要有一定的爆发力,又要有动作的高度精确,要做到眼到、手到和步伐到,提高了身体的协调和平衡能力.不管学习还是工作,每天都或多或少有点压抑,打球能使大脑的兴奋与抑制过程合理交替,避免神经系统过度紧张.某中学对学生参加乒乓球运动的情况进行调查,将每周参加乒乓球运动超过2小时的学生称为“乒乓球爱好者”,否则称为“非乒乓球爱好者”,从调查结果中随机抽取100份进行分析,得到数据如表所示:
(1)补全 列联表,并判断我们能否有
列联表,并判断我们能否有 的把握认为是否为“乒乓球爱好者”与性别有关?
的把握认为是否为“乒乓球爱好者”与性别有关?
(2)为了解学生的乒乓球运动水平,现从抽取的“乒乓球爱好者”学生中按性别采用分层抽样的方法抽取3人,与体育老师进行乒乓球比赛,其中男乒乓球爱好者获胜的概率为 ,女乒乓球爱好者获胜的概率为
,女乒乓球爱好者获胜的概率为 ,每次比赛结果相互独立,记这3人获胜的人数为X,求X的分布列和数学期望.
,每次比赛结果相互独立,记这3人获胜的人数为X,求X的分布列和数学期望.
参考公式: ,
, .
.
乒乓球爱好者 | 非乒乓球爱好者 | 总计 | |
男 | 40 | 56 | |
女 | 24 | ||
总计 | 100 |
(1)补全
 列联表,并判断我们能否有
列联表,并判断我们能否有 的把握认为是否为“乒乓球爱好者”与性别有关?
的把握认为是否为“乒乓球爱好者”与性别有关?(2)为了解学生的乒乓球运动水平,现从抽取的“乒乓球爱好者”学生中按性别采用分层抽样的方法抽取3人,与体育老师进行乒乓球比赛,其中男乒乓球爱好者获胜的概率为
 ,女乒乓球爱好者获胜的概率为
,女乒乓球爱好者获胜的概率为 ,每次比赛结果相互独立,记这3人获胜的人数为X,求X的分布列和数学期望.
,每次比赛结果相互独立,记这3人获胜的人数为X,求X的分布列和数学期望.参考公式:
 ,
, .
.
| 0.05 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-03-20更新
|
550次组卷
|
7卷引用:辽宁省本溪市第一中学2023-2024学年高二下学期寒假验收考试数学试题
辽宁省本溪市第一中学2023-2024学年高二下学期寒假验收考试数学试题(已下线)9.2 独立性检验(五大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)辽宁省大连金石高级中学、志德高级中学中2023-2024学年高二下学期4月考试数学试卷(已下线)模块一 专题1 《线性回归与相关性和独立性检验》(北师大版高二期中)B拔高卷(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(6)辽宁省朝阳市2022-2023学年高二下学期期末数学试题辽宁省朝阳市建平县2022-2023学年高二下学期期末数学试题