名校
1 . 英国物理学家牛顿用“作切线”的方法求函数零点时,给出了“牛顿数列”,它在航空航天中应用非常广泛.其定义是:对于函数 ,若满足
,若满足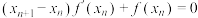 ,则称数列
,则称数列 为牛顿数列.已知
为牛顿数列.已知 ,在横坐标为
,在横坐标为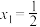 的点处作
的点处作 的切线,切线与
的切线,切线与 轴交点的横坐标为
轴交点的横坐标为 ,继续牛顿法的操作得到数列
,继续牛顿法的操作得到数列 .设
.设 ,数列
,数列 的前
的前 项积为
项积为 .若对任意的
.若对任意的 恒成立,则整数
恒成立,则整数 的最小值为
的最小值为_____________ .
 ,若满足
,若满足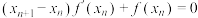 ,则称数列
,则称数列 为牛顿数列.已知
为牛顿数列.已知 ,在横坐标为
,在横坐标为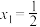 的点处作
的点处作 的切线,切线与
的切线,切线与 轴交点的横坐标为
轴交点的横坐标为 ,继续牛顿法的操作得到数列
,继续牛顿法的操作得到数列 .设
.设 ,数列
,数列 的前
的前 项积为
项积为 .若对任意的
.若对任意的 恒成立,则整数
恒成立,则整数 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
2 . 欧拉恒等式 (
( 为虚数单位,
为虚数单位, 为自然对数的底数)被称为数学中最奇妙的公式.它是复分析中欧拉公式
为自然对数的底数)被称为数学中最奇妙的公式.它是复分析中欧拉公式 的特例:当自变量
的特例:当自变量 时,
时,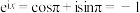 ,得
,得 .根据欧拉公式,复数
.根据欧拉公式,复数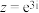 在复平面上所对应的点在( )
在复平面上所对应的点在( )
 (
( 为虚数单位,
为虚数单位, 为自然对数的底数)被称为数学中最奇妙的公式.它是复分析中欧拉公式
为自然对数的底数)被称为数学中最奇妙的公式.它是复分析中欧拉公式 的特例:当自变量
的特例:当自变量 时,
时,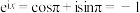 ,得
,得 .根据欧拉公式,复数
.根据欧拉公式,复数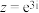 在复平面上所对应的点在( )
在复平面上所对应的点在( )| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
您最近一年使用:0次
2024-07-20更新
|
126次组卷
|
3卷引用:福建省福州市闽侯县闽江口协作校(七校)2023-2024学年高一下学期7月期末联考数学试题
3 . 在“杨辉三角”中,每一个数都是它“肩上”两个数的和,它开头几行如图所示.那么,在“杨辉三角”中,第_____________ 行会出现三个相邻的数,其比为2:3:4.

您最近一年使用:0次
解题方法
4 . 我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”有一个题目:“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里,里法三百步.欲知为田几何?”其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实;一为从隅,开平方得积.”这就是秦九韶推出的“三斜求积”公式.若 的内角
的内角 的对应边分别为
的对应边分别为 ,面积为
,面积为 ,则“三斜求积”公式为
,则“三斜求积”公式为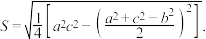
(1)用“三斜求积”公式证明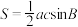 ;
;
(2)若 ,且
,且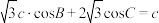 ,求
,求 面积的最大值;
面积的最大值;
(3)定义:四面体中,若异面棱长相等的四面体为等腰四面体.设等腰四面体 的外接球表面积为
的外接球表面积为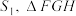 的外接圆面积为
的外接圆面积为 .已知
.已知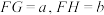 ,且
,且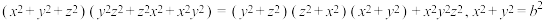 ,
,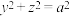 ,试用
,试用 表示
表示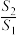 ,并求
,并求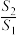 的取值范围.
的取值范围.
 的内角
的内角 的对应边分别为
的对应边分别为 ,面积为
,面积为 ,则“三斜求积”公式为
,则“三斜求积”公式为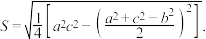
(1)用“三斜求积”公式证明
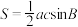 ;
;(2)若
 ,且
,且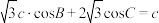 ,求
,求 面积的最大值;
面积的最大值;(3)定义:四面体中,若异面棱长相等的四面体为等腰四面体.设等腰四面体
 的外接球表面积为
的外接球表面积为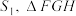 的外接圆面积为
的外接圆面积为 .已知
.已知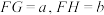 ,且
,且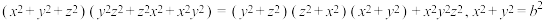 ,
,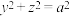 ,试用
,试用 表示
表示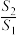 ,并求
,并求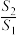 的取值范围.
的取值范围.
您最近一年使用:0次
5 . 威镇阁坐落于漳州市区战备大桥引桥左侧,是漳州市的标志性建筑之一.某同学为测量威镇阁的高度 ,在威镇阁的正北方向找到一座建筑物
,在威镇阁的正北方向找到一座建筑物 ,高约为
,高约为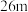 ,在地面上点
,在地面上点 处(
处(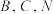 三点共线)测得建筑物顶部
三点共线)测得建筑物顶部 ,威镇阁顶部
,威镇阁顶部 的仰角分别为
的仰角分别为 和
和 ,在
,在 处测得威镇阁顶部
处测得威镇阁顶部 的仰角为
的仰角为 ,威镇阁的高度约为( )
,威镇阁的高度约为( )
 ,在威镇阁的正北方向找到一座建筑物
,在威镇阁的正北方向找到一座建筑物 ,高约为
,高约为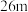 ,在地面上点
,在地面上点 处(
处(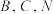 三点共线)测得建筑物顶部
三点共线)测得建筑物顶部 ,威镇阁顶部
,威镇阁顶部 的仰角分别为
的仰角分别为 和
和 ,在
,在 处测得威镇阁顶部
处测得威镇阁顶部 的仰角为
的仰角为 ,威镇阁的高度约为( )
,威镇阁的高度约为( )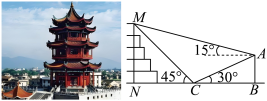
A.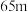 | B.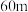 | C.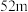 | D. |
您最近一年使用:0次
6 . 《九章算术》中将正四棱台(上、下底面均为正方形)称为“方亭”.现有一方亭,上底面边长为2,下底面边长为4,侧棱与下底面所成的角为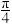 ,则此方亭的体积为( )
,则此方亭的体积为( )
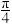 ,则此方亭的体积为( )
,则此方亭的体积为( )A.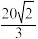 | B.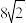 |
C.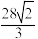 | D.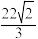 |
您最近一年使用:0次
2024-07-07更新
|
315次组卷
|
3卷引用:福建省福州市九县(市、区)一中2023-2024学年高一下学期7月期末联考数学试题
福建省福州市九县(市、区)一中2023-2024学年高一下学期7月期末联考数学试题(已下线)专题5 角的大小 作角转化(经典好题母题)【练】山西省山西大学附属中学校2024-2025学年高二上学期9月模块诊断考试数学试题
7 . 国家二级文化保护遗址玉皇阁的台基可近似看作上、下底面边长分别为 ,
,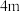 ,侧棱长为
,侧棱长为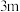 的正四棱台,则该台基的体积约为( )
的正四棱台,则该台基的体积约为( )
 ,
,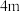 ,侧棱长为
,侧棱长为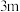 的正四棱台,则该台基的体积约为( )
的正四棱台,则该台基的体积约为( )A.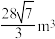 | B.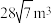 | C.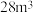 | D.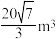 |
您最近一年使用:0次
2024-06-04更新
|
1033次组卷
|
6卷引用:福建省部分学校教学联盟2023~2024学年高一下学期期末质量检测数学试题
8 . 我国汉代数学家赵爽为了证明勾股定理,创造了一幅“勾股圆方图”,后人称其为“赵爽弦图”.类比赵爽弦图,用3个全等的小三角形拼成了如图所示的等边 ,若
,若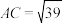 ,
,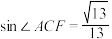 ,则
,则
__________ .
 ,若
,若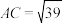 ,
,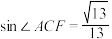 ,则
,则

您最近一年使用:0次
2024-05-27更新
|
559次组卷
|
3卷引用:福建省泉州市2023-2024学年高一下学期期末质量检测数学模拟训练试题(3)
解题方法
9 . 《算学启蒙》作者是元代著名数学家朱世杰,这是一部在中国乃至世界最早的科学普及著作.里面涉及一些“堆垛”问题,主要利用“堆垛”研究数列以及数列的求和问题.某同学模仿“堆垛”问题,将108根相同的铅笔刚好全部堆放成纵断面为等腰梯形的“垛”,要求层数不小于2,且从上往下,每一层比下一层少1根,则该“等腰梯形垛”最多可以堆放__________ 层.
您最近一年使用:0次
名校
解题方法
10 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程为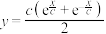 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数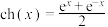 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正、余弦函数导数之间的关系,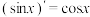 ,
,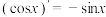 ,请写出
,请写出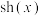 ,
,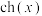 具有的类似的性质(不需要证明);
具有的类似的性质(不需要证明);
(2)当 时,
时,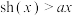 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求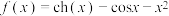 的最小值.
的最小值.
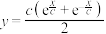 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数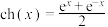 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正、余弦函数导数之间的关系,
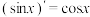 ,
,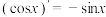 ,请写出
,请写出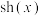 ,
,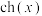 具有的类似的性质(不需要证明);
具有的类似的性质(不需要证明);(2)当
 时,
时,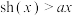 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)求
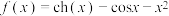 的最小值.
的最小值.
您最近一年使用:0次
2024-03-10更新
|
1351次组卷
|
22卷引用:福建省龙岩市上杭县第一中学2023-2024学年高二下学期数学期末复习卷试题(八)
福建省龙岩市上杭县第一中学2023-2024学年高二下学期数学期末复习卷试题(八)福建省龙岩市连城县第一中学2023-2024学年高二下学期5月月考(2)数学试题河南省三门峡市2023-2024学年高二下学期5月期末调研考试数学试题辽宁省锦州市2023-2024学年高二下学期期末考试数学试卷福建省泉州市泉州科技中学2023-2024学年高二下学期第一次月考数学试题广西示范性高中2023-2024学年高二下学期3月调研测试数学试卷(已下线)模块一 专题3 导数在研究函数极值和最值中的应用(B)(已下线)综合检测卷(数列+导数)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)湖北省荆州市沙市中学2023-2024学年高二下学期3月月考数学试题广东省揭阳市惠来县第一中学2023-2024学年高二下学期3月月考数学试题(已下线)模块四 专题1 高考新题型专练(新定义专练)(人教A)(高二)(已下线)高二下学期第一次月考模拟卷(新题型)(导数+计数原理)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019)河北省正定中学2023-2024学年高二下学期第一次月考数学试题河北省邯郸市大名县第一中学2023-2024学年高二下学期3月月考数学试卷山东省临沂市第二十四中学2023-2024学年高二下学期3月月考数学试题吉林省长春外国语学校2023-2024学年高二下学期4月月考数学试卷(已下线)模块一 专题3 《导数在研究函数极值和最值中的应用》B提升卷(苏教版)(已下线)模块三 专题3 高考新题型专练 专题2 新定义专练(苏教版)广东省深圳市高级中学(集团)2023-2024学年高二下学期期中考试数学试卷(已下线)上海市四校(复兴高级中学、松江二中、奉贤中学、金山中学)2024届高三下学期3月联考数学试题变式题17-21四川省广元市川师大万达中学2023-2024学年高二下学期6月月考数学试题江苏省南京田家炳高级中学2023-2024学年高二下学期3月模拟考试数学试卷



