名校
解题方法
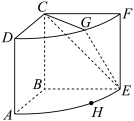
1 . 如图,几何体是以正方形ABCD的一边BC所在直线为旋转轴,其余三边旋转90°形成的面所围成的几何体,点G是圆弧 的中点,点H是圆弧
的中点,点H是圆弧 上的动点,
上的动点, ,给出下列四个结论:
,给出下列四个结论:
①不存在点H,使得平面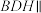 平面CEG;
平面CEG;
②存在点H,使得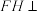 平面CEG;
平面CEG;
③不存在点H,使得点H到平面CEG的距离大于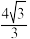 ;
;
④存在点H,使得直线DH与平而CEG所成角的正弦值为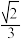 .
.
其中所有正确结论的序号是____________ .
 的中点,点H是圆弧
的中点,点H是圆弧 上的动点,
上的动点, ,给出下列四个结论:
,给出下列四个结论:①不存在点H,使得平面
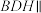 平面CEG;
平面CEG;②存在点H,使得
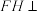 平面CEG;
平面CEG;③不存在点H,使得点H到平面CEG的距离大于
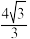 ;
;④存在点H,使得直线DH与平而CEG所成角的正弦值为
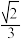 .
.其中所有正确结论的序号是
您最近一年使用:0次
2024-05-10更新
|
730次组卷
|
3卷引用:北京市通州区2024届高三下学期二模数学试题
2 . 如图,正方形 和矩形
和矩形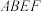 所在的平面互相垂直.点
所在的平面互相垂直.点 在正方形
在正方形 及其内部运动,点
及其内部运动,点 在矩形
在矩形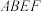 及其内部运动.设
及其内部运动.设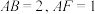 ,给出下列四个结论:
,给出下列四个结论: ,使
,使 ;
;
②存在点 ,使
,使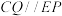 ;
;
③到直线 和
和 的距离相等的点
的距离相等的点 有无数个;
有无数个;
④若 ,则四面体
,则四面体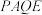 体积的最大值为
体积的最大值为 .
.
其中所有正确结论的序号是__________ .
 和矩形
和矩形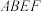 所在的平面互相垂直.点
所在的平面互相垂直.点 在正方形
在正方形 及其内部运动,点
及其内部运动,点 在矩形
在矩形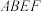 及其内部运动.设
及其内部运动.设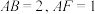 ,给出下列四个结论:
,给出下列四个结论:
 ,使
,使 ;
;②存在点
 ,使
,使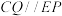 ;
;③到直线
 和
和 的距离相等的点
的距离相等的点 有无数个;
有无数个;④若
 ,则四面体
,则四面体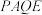 体积的最大值为
体积的最大值为 .
.其中所有正确结论的序号是
您最近一年使用:0次
2024-04-08更新
|
1099次组卷
|
3卷引用:北京市西城区2024届高三下学期统一测试(一模)数学试卷
名校
解题方法
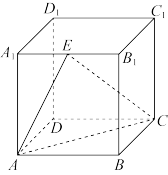
3 . 如图,在正方体 ,中,
,中, ,
, 分别为线段
分别为线段 ,
, 上的动点.给出下列四个结论:
上的动点.给出下列四个结论:
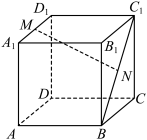
①存在点 ,存在点
,存在点 ,满足
,满足 ∥平面
∥平面 ;
;
②任意点 ,存在点
,存在点 ,满足
,满足 ∥平面
∥平面 ;
;
③任意点 ,存在点
,存在点 ,满足
,满足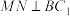 ;
;
④任意点 ,存在点
,存在点 ,满足
,满足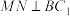 .
.
其中所有正确结论的序号是__________ .
 ,中,
,中, ,
, 分别为线段
分别为线段 ,
, 上的动点.给出下列四个结论:
上的动点.给出下列四个结论:
①存在点
 ,存在点
,存在点 ,满足
,满足 ∥平面
∥平面 ;
;②任意点
 ,存在点
,存在点 ,满足
,满足 ∥平面
∥平面 ;
;③任意点
 ,存在点
,存在点 ,满足
,满足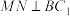 ;
;④任意点
 ,存在点
,存在点 ,满足
,满足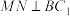 .
.其中所有正确结论的序号是
您最近一年使用:0次
2023-06-02更新
|
2197次组卷
|
10卷引用:北京大兴精华学校2023届高三高考适应性测试数学试题
北京大兴精华学校2023届高三高考适应性测试数学试题北京市东直门中学2024届高三考前练习数学试卷(已下线)专题10 空间向量与立体几何-3(已下线)模块一 情境7 以立体几何为背景(已下线)第05讲 空间向量及其应用(练习)(已下线)信息必刷卷01广东省东莞市东华高级中学、东华松山湖高级中学2022-2023学年高二下学期期末学习效率检测数学试题云南省保山市智源高级中学2023-2024学年高二下学期第二次(6月)月考数学试题宁夏青铜峡市宁朔中学2024-2025学年高二上学期9月月考数学试题(已下线)第三节 直线、平面平行的判定与性质【讲】北京专版
解题方法
4 . 如图所示,在正方体 中,
中, 是棱
是棱 上一点,平面
上一点,平面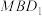 与棱
与棱 交于点
交于点 .给出下面几个结论:
.给出下面几个结论: 是平行四边形;
是平行四边形;
②四边形 可能是正方形;
可能是正方形;
③存在平面 与直线
与直线 垂直;
垂直;
④任意平面 与平面
与平面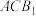 垂直;
垂直;
⑤平面 与平面
与平面 夹角余弦的最大值为
夹角余弦的最大值为 .
.
其中所有正确结论的序号是_______ .
 中,
中, 是棱
是棱 上一点,平面
上一点,平面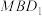 与棱
与棱 交于点
交于点 .给出下面几个结论:
.给出下面几个结论: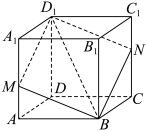
 是平行四边形;
是平行四边形;②四边形
 可能是正方形;
可能是正方形;③存在平面
 与直线
与直线 垂直;
垂直;④任意平面
 与平面
与平面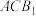 垂直;
垂直;⑤平面
 与平面
与平面 夹角余弦的最大值为
夹角余弦的最大值为 .
.其中所有正确结论的序号是
您最近一年使用:0次
2023-05-10更新
|
1470次组卷
|
7卷引用:北京市房山区2023届高三二模数学试题
北京市房山区2023届高三二模数学试题北京卷专题19B空间向量与立体几何(选择填空题)(已下线)1.4.1 用空间向量研究直线、平面的位置关系(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)(已下线)高二上学期期中考试填空题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)新疆阿克苏地区库车市第二中学2023-2024学年高二上学期第一次月数学试题(已下线)3.4.1 判断空间直线、平面的位置关系(六大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)(已下线)8.6.3平面与平面垂直——课后作业(提升版)
名校
解题方法
5 . 如图,在长方体 中,
中,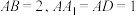 ,动点
,动点 分别在线段
分别在线段 和
和 上.给出下列四个结论:
上.给出下列四个结论:
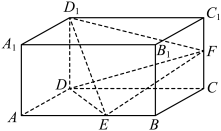
①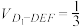 ;
;
②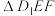 不可能是等边三角形;
不可能是等边三角形;
③当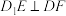 时,
时, ;
;
④至少存在两组 ,使得三棱锥
,使得三棱锥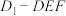 的四个面均为直角三角形.
的四个面均为直角三角形.
其中所有正确结论的序号是__________ .
 中,
中,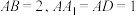 ,动点
,动点 分别在线段
分别在线段 和
和 上.给出下列四个结论:
上.给出下列四个结论:
①
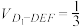 ;
;②
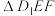 不可能是等边三角形;
不可能是等边三角形;③当
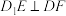 时,
时, ;
;④至少存在两组
 ,使得三棱锥
,使得三棱锥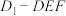 的四个面均为直角三角形.
的四个面均为直角三角形.其中所有正确结论的序号是
您最近一年使用:0次
2023-05-07更新
|
1240次组卷
|
6卷引用:北京市昌平区2023届高三二模数学试题
北京市昌平区2023届高三二模数学试题北京卷专题19B空间向量与立体几何(选择填空题)(已下线)北京市第四中学2024届高三上学期开学测试数学试题(已下线)2024年全国高考名校名师联席命制数学(理)信息卷(十)(已下线)专题01 空间向量与立体几何(6)四川省宜宾市兴文第二中学校2024届高三下学期开学考试数学(理)试题
名校
解题方法
6 . 如图,在正方体 中,
中, 是
是 的中点,平面
的中点,平面 将正方体分成体积分别为
将正方体分成体积分别为 ,
, (
( ) 的两部分,则
) 的两部分,则
_______
 中,
中, 是
是 的中点,平面
的中点,平面 将正方体分成体积分别为
将正方体分成体积分别为 ,
, (
( ) 的两部分,则
) 的两部分,则
您最近一年使用:0次
2023-05-05更新
|
2577次组卷
|
10卷引用:北京市东城区2023届高三二模数学试题
北京市东城区2023届高三二模数学试题(已下线)上海市华东师范大学第二附属中学2023届高三三模数学试题湖南省永州市宁远县第二中学2022-2023学年高一下学期5月质量检测数学试题辽宁省沈阳市第一二〇中学2022-2023学年高一下学期第三次质量监测数学试题(已下线)第七章 立体几何与空间向量 第三节?第一课时直线,平面平行的判定与性质(A素养养成卷)辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学试题(已下线)周测14 空间几何体及其体积和表面积 (一轮好卷北京专版 )(已下线)周测15 空间平行与垂直的关系(北京专版 )(已下线)第一节 基本立体图形及表面积与体积【讲】(高三大一轮基础版)(已下线)第三节 直线、平面平行的判定与性质【同步课时】北京专项
名校
解题方法
7 . 如图,在直角梯形 中,E为
中,E为 的中点,
的中点, ,
,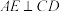 ,M,N分别是
,M,N分别是 ,
, 的中点,将
的中点,将 沿
沿 折起,使点D不在平面
折起,使点D不在平面 内,则下命题中正确的序号为
内,则下命题中正确的序号为______ .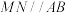 ;
;
②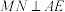 ;
;
③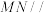 平面
平面 ;
;
④存在某折起位置,使得平面 平面
平面 .
.
 中,E为
中,E为 的中点,
的中点, ,
,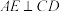 ,M,N分别是
,M,N分别是 ,
, 的中点,将
的中点,将 沿
沿 折起,使点D不在平面
折起,使点D不在平面 内,则下命题中正确的序号为
内,则下命题中正确的序号为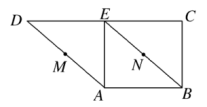
 ;
;②
 ;
;③
 平面
平面 ;
;④存在某折起位置,使得平面
 平面
平面 .
.
您最近一年使用:0次
2023-03-29更新
|
1901次组卷
|
11卷引用:北京市八一学校2023届高三模拟测试数学试题
北京市八一学校2023届高三模拟测试数学试题北京市汇文中学教育集团2023-2024学年高三下学期开学考数学试题(已下线)第四节 直线、平面垂直的判定及性质【同步课时】北京专项 (已下线)1.4.1 用空间向量研究直线、平面的位置关系(AB分层训练)-【冲刺满分】2023-2024学年高二数学重难点突破+分层训练同步精讲练(人教A版2019选择性必修第一册)(已下线)第七章 立体几何与空间向量 第五节 空间向量与线、面位置关系(B素养提升卷)(已下线)第一章 点线面位置关系 专题二 空间垂直关系的判定与证明 微点2 空间直线垂直的判定与证明综合训练【培优版】(已下线)1.4.1 用空间向量研究直线、平面的位置关系【第三练】(已下线)3.4.1 判断空间直线、平面的位置关系(六大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)(已下线)第05讲 空间向量的应用(一)-【暑假预科讲义】(人教A版2019选择性必修第一册)(已下线)6.2 空间几何中的平行与垂直(已下线)空间直线、平面的垂直-一轮复习考点专练
名校
解题方法
8 . 如图,在棱长为 的正方体
的正方体 中,点
中,点 ,
, 分别在线段
分别在线段 和
和 上.
上.
① 的最小值为
的最小值为 ;
;
②四面体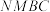 的体积为
的体积为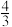 ;
;
③有且仅有一条直线 与
与 垂直;
垂直;
④存在点 ,
, ,使
,使 为等边三角形.
为等边三角形.
其中所有正确结论的序号是____ .
 的正方体
的正方体 中,点
中,点 ,
, 分别在线段
分别在线段 和
和 上.
上.
①
 的最小值为
的最小值为 ;
;②四面体
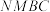 的体积为
的体积为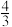 ;
;③有且仅有一条直线
 与
与 垂直;
垂直;④存在点
 ,
, ,使
,使 为等边三角形.
为等边三角形.其中所有正确结论的序号是
您最近一年使用:0次
2023-03-27更新
|
2228次组卷
|
10卷引用:北京市西城区2023届高三一模数学试题
北京市西城区2023届高三一模数学试题专题12压轴题汇总(10、15、21题)专题08空间向量与立体几何北京卷专题19B空间向量与立体几何(选择填空题)北京市昌平区第一中学2024届高三上学期期中考试数学试题北京市陈经纶中学2023-2024学年高三上学期数学阶段性诊断练习6北京市顺义区第一中学2024-2025学年高三上学期期中考试数学试卷宁夏银川一中2022-2023学年高二下学期期中考试数学(理)试题(已下线)专题02 空间向量与空间角、空间距离【考题猜想】-2023-2024学年高二数学上学期期中考点大串讲(人教A版2019选择性必修第一册)(已下线)高二上期中真题精选(易错60题30个考点专练)【考题猜想】-2023-2024学年高二数学上学期期中考点大串讲(人教A版2019选择性必修第一册)
名校
解题方法
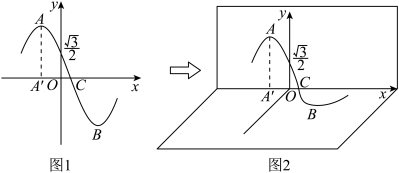
9 . 已知函数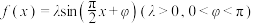 的部分图象如图1所示,
的部分图象如图1所示, 、
、 分别为图象的最高点和最低点,过
分别为图象的最高点和最低点,过 作
作 轴的垂线,交
轴的垂线,交 轴于
轴于 ,点
,点 为该部分图象与
为该部分图象与 轴的交点.将绘有该图象的纸片沿
轴的交点.将绘有该图象的纸片沿 轴折成直二面角,如图2所示,此时
轴折成直二面角,如图2所示,此时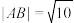 ,则
,则
______ .
①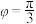 ;
;
②图2中,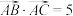 ;
;
③图2中,过线段 的中点且与
的中点且与 垂直的平面与
垂直的平面与 轴交于点
轴交于点 ;
;
④图2中, 是
是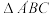 及其内部的点构成的集合.设集合
及其内部的点构成的集合.设集合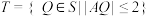 ,则
,则 表示的区域的面积大于
表示的区域的面积大于 .
.
其中所有正确结论的序号是______ .
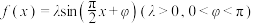 的部分图象如图1所示,
的部分图象如图1所示, 、
、 分别为图象的最高点和最低点,过
分别为图象的最高点和最低点,过 作
作 轴的垂线,交
轴的垂线,交 轴于
轴于 ,点
,点 为该部分图象与
为该部分图象与 轴的交点.将绘有该图象的纸片沿
轴的交点.将绘有该图象的纸片沿 轴折成直二面角,如图2所示,此时
轴折成直二面角,如图2所示,此时 ,则
,则
①
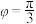 ;
;②图2中,
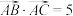 ;
;③图2中,过线段
 的中点且与
的中点且与 垂直的平面与
垂直的平面与 轴交于点
轴交于点 ;
;④图2中,
 是
是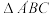 及其内部的点构成的集合.设集合
及其内部的点构成的集合.设集合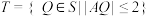 ,则
,则 表示的区域的面积大于
表示的区域的面积大于 .
.其中所有正确结论的序号是
您最近一年使用:0次
2023-03-27更新
|
2543次组卷
|
14卷引用:北京市东城区2023届高三一模数学试题
北京市东城区2023届高三一模数学试题专题12压轴题汇总(10、15、21题)专题03三角函数与解三角形专题08空间向量与立体几何北京卷专题06三角函数(填空题)北京工业大学附属中学2022-2023学年高一下学期期中考试数学试题北京市海淀区首都师范大学附属中学2024届高三上学期10月阶段检测数学试题北京高一专题09立体几何北京市育英学校2024-2025学年高三上学期10月月考数学试卷(已下线)模块七 第6套 迎接高考之必做基础热身题( 概率与立几)新疆乌鲁木齐市第一中学2024届高三上学期第二次月考数学试题(已下线)空间向量与立体几何(已下线)第8题 由空间距离求夹角(压轴小题)(已下线)重组3 高二期中真题重组卷(广东卷)B提升卷
10 . 已知正方体 的棱长为1,
的棱长为1, 是空间中任意一点.给出下列四个结论:
是空间中任意一点.给出下列四个结论:
①若点 在线段
在线段 上运动,则始终有
上运动,则始终有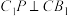 ;
;
②若点 在线段
在线段 上运动,则过
上运动,则过 ,
, ,
, 三点的正方体截面面积的最小值为
三点的正方体截面面积的最小值为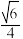 ;
;
③若点 在线段
在线段 上运动,三棱锥
上运动,三棱锥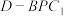 体积为定值;
体积为定值;
④若点 在线段
在线段 上运动,则
上运动,则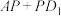 的最小值为
的最小值为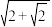 .
.
其中所有正确结论的序号有
您最近一年使用:0次
2023-03-22更新
|
1411次组卷
|
8卷引用:北京市第四中学2023届高三阶段性考试(零模)数学试题
(已下线)北京市第四中学2023届高三阶段性考试(零模)数学试题北京市回民学校2023届高三下学期数学统测试题(四)北京市第一六一中学2023-2024学年高三下学期开学测试数学试卷北京市顺义区杨镇第一中学2024届高三下学期3月检测数学试题(已下线)高二上学期第一次月考填空题压轴题50题专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)重庆市涪陵区部分学校2023-2024学年高二上学期第一次月考数学试题(已下线)第一次月考检测模拟试卷(原卷版)(已下线)专题01 空间向量与立体几何(5)



