名校
解题方法
1 . 如图,在边长为1的正△ABC中,E,F分别是边AB,AC上的点,若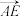 =m
=m ,
,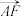 =n
=n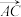 ,m,n∈(0,1).设EF的中点为M,BC的中点为N.
,m,n∈(0,1).设EF的中点为M,BC的中点为N.
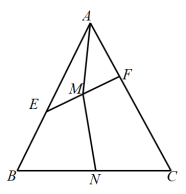
(1)若A,M,N三点共线,求证:m=n;
(2)若m+n=1,求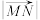 的最小值.
的最小值.
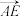 =m
=m ,
,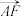 =n
=n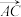 ,m,n∈(0,1).设EF的中点为M,BC的中点为N.
,m,n∈(0,1).设EF的中点为M,BC的中点为N.
(1)若A,M,N三点共线,求证:m=n;
(2)若m+n=1,求
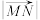 的最小值.
的最小值.
您最近一年使用:0次
2021-10-20更新
|
722次组卷
|
12卷引用:专题6.4 平面向量的应用--几何、物理(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)
(已下线)专题6.4 平面向量的应用--几何、物理(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)江苏省苏州市三中2020-2021学年高一下学期3月月考数学试题江苏省镇江市第一中学2020-2021学年高一下学期期中数学试题山东省枣庄市薛城区2020-2021学年高一下学期期中考试数学试题山东省枣庄市第八中学2020-2021学年高一下学期期中考试数学试题(已下线)8.1 向量的概念和线性运算(作业)-【上好课】2020-2021学年高一数学下册同步备课系列(沪教版2020必修第二册)上海市第二中学2019-2020学年高二上学期期中数学试题四川省眉山市彭山区第一中学2019-2020学年高一下学期期中考试数学试题山东省济宁市兖州区2021-2022学年高一下学期期中数学试题沪教版(2020) 一轮复习 堂堂清 第六单元 6.2 向量的分解定理山东省滨州市博兴县第二中学2022-2023学年高一下学期第二次月考数学试题四川省凉山州民族中学2023-2024学年高一下学期3月月考数学试题
名校
解题方法
2 . 已知函数 ,
,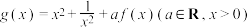 .
.
(1)求 的值域;
的值域;
(2)讨论 在
在 上的单调性;
上的单调性;
(3)设 ,
,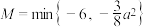 ,证明:
,证明: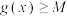 .
.
 ,
,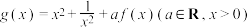 .
.(1)求
 的值域;
的值域;(2)讨论
 在
在 上的单调性;
上的单调性;(3)设
 ,
,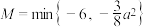 ,证明:
,证明: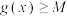 .
.
您最近一年使用:0次
解题方法
3 . 已知函数 .
.
(1)求 的定义域和值域.
的定义域和值域.
(2)用定义法证明:函数 在
在 上是减函数.
上是减函数.
 .
.(1)求
 的定义域和值域.
的定义域和值域.(2)用定义法证明:函数
 在
在 上是减函数.
上是减函数.
您最近一年使用:0次
解题方法
4 . 已知 ,且函数 .
.
(1)判断 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)设 ,对任意的
,对任意的 ,总存在
,总存在 ,使得g(x1)=h(x2)成立,求实数c的取值范围.
,使得g(x1)=h(x2)成立,求实数c的取值范围.
在以下①,②两个条件中,选择一个条件,将上面的题目补充完整,先求出a,b的值,并解答本题.
①函数 在定义域
在定义域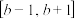 上为偶函数;
上为偶函数;
②函数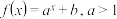 在
在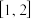 上的值域为
上的值域为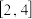 ;
;
 .
.(1)判断
 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;(2)设
 ,对任意的
,对任意的 ,总存在
,总存在 ,使得g(x1)=h(x2)成立,求实数c的取值范围.
,使得g(x1)=h(x2)成立,求实数c的取值范围.在以下①,②两个条件中,选择一个条件,将上面的题目补充完整,先求出a,b的值,并解答本题.
①函数
 在定义域
在定义域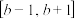 上为偶函数;
上为偶函数;②函数
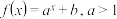 在
在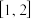 上的值域为
上的值域为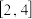 ;
;
您最近一年使用:0次



