名校
解题方法
1 . 若函数 与
与 满足:对任意的
满足:对任意的 ,总存在唯一的
,总存在唯一的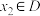 ,使
,使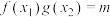 成立,则称
成立,则称 是
是 在区间
在区间 上的“
上的“ 阶伴随函数”;当
阶伴随函数”;当 时,则称
时,则称 为区间
为区间 上的“m阶自伴函数”.
上的“m阶自伴函数”.
(1)判断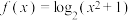 是否为区间
是否为区间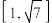 上的“2阶自伴函数”?并说明理由;
上的“2阶自伴函数”?并说明理由;
(2)若函数 为区间
为区间 上的“1阶自伴函数”,求
上的“1阶自伴函数”,求 的值;
的值;
(3)若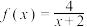 是
是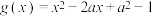 在区间
在区间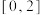 上的“2阶伴随函数”,求实数
上的“2阶伴随函数”,求实数 的取值范围.
的取值范围.
 与
与 满足:对任意的
满足:对任意的 ,总存在唯一的
,总存在唯一的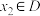 ,使
,使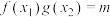 成立,则称
成立,则称 是
是 在区间
在区间 上的“
上的“ 阶伴随函数”;当
阶伴随函数”;当 时,则称
时,则称 为区间
为区间 上的“m阶自伴函数”.
上的“m阶自伴函数”.(1)判断
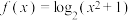 是否为区间
是否为区间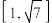 上的“2阶自伴函数”?并说明理由;
上的“2阶自伴函数”?并说明理由;(2)若函数
 为区间
为区间 上的“1阶自伴函数”,求
上的“1阶自伴函数”,求 的值;
的值;(3)若
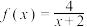 是
是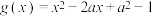 在区间
在区间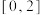 上的“2阶伴随函数”,求实数
上的“2阶伴随函数”,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知函数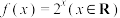 ,记
,记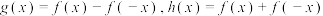 .
.
(1)求不等式的解集: ;
;
(2)设 为实数,若存在实数
为实数,若存在实数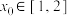 ,使得
,使得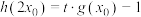 成立,求
成立,求 的取值范围;
的取值范围;
(3)记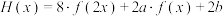 (其中
(其中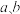 均为实数),若对于任意的
均为实数),若对于任意的 ,均有
,均有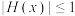 ,求
,求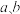 的值.
的值.
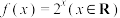 ,记
,记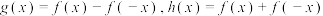 .
.(1)求不等式的解集:
 ;
;(2)设
 为实数,若存在实数
为实数,若存在实数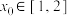 ,使得
,使得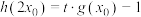 成立,求
成立,求 的取值范围;
的取值范围;(3)记
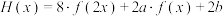 (其中
(其中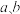 均为实数),若对于任意的
均为实数),若对于任意的 ,均有
,均有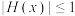 ,求
,求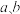 的值.
的值.
您最近一年使用:0次
名校
解题方法
3 . 设 是一个定义域为
是一个定义域为 的函数.若
的函数.若 是
是 的一个非空子集,且对于任意的
的一个非空子集,且对于任意的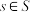 ,都有
,都有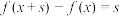 ,则称
,则称 是
是 关联的.
关联的.
(1)判断函数 和函数
和函数 是否是
是否是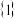
 关联的,无需说明理由.(
关联的,无需说明理由.( 表示不超过
表示不超过 的最大整数)
的最大整数)
(2)若函数 是
是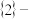 关联的,且在
关联的,且在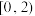 上,
上, ,解不等式
,解不等式 .
.
(3)已知正实数 满足
满足 ,且函数
,且函数 是
是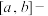 关联的,求
关联的,求 的解析式.
的解析式.
 是一个定义域为
是一个定义域为 的函数.若
的函数.若 是
是 的一个非空子集,且对于任意的
的一个非空子集,且对于任意的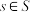 ,都有
,都有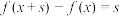 ,则称
,则称 是
是 关联的.
关联的.(1)判断函数
 和函数
和函数 是否是
是否是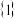
 关联的,无需说明理由.(
关联的,无需说明理由.( 表示不超过
表示不超过 的最大整数)
的最大整数)(2)若函数
 是
是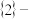 关联的,且在
关联的,且在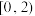 上,
上, ,解不等式
,解不等式 .
.(3)已知正实数
 满足
满足 ,且函数
,且函数 是
是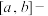 关联的,求
关联的,求 的解析式.
的解析式.
您最近一年使用:0次
名校
4 . 已知函数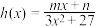 为奇函数,
为奇函数,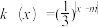 ,其中
,其中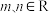 .
.
(1)若函数h(x)的图象过点A(1,1),求实数m和n的值;
(2)若m=3,试判断函数 在
在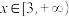 上的单调性并证明;
上的单调性并证明;
(3)设函数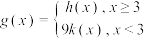 ,若对每一个不小于3的实数
,若对每一个不小于3的实数 ,都恰有一个小于3的实数
,都恰有一个小于3的实数 ,使得
,使得 成立,求实数m的取值范围.
成立,求实数m的取值范围.
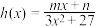 为奇函数,
为奇函数,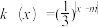 ,其中
,其中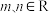 .
.(1)若函数h(x)的图象过点A(1,1),求实数m和n的值;
(2)若m=3,试判断函数
 在
在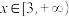 上的单调性并证明;
上的单调性并证明;(3)设函数
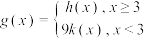 ,若对每一个不小于3的实数
,若对每一个不小于3的实数 ,都恰有一个小于3的实数
,都恰有一个小于3的实数 ,使得
,使得 成立,求实数m的取值范围.
成立,求实数m的取值范围.
您最近一年使用:0次
2022-03-27更新
|
949次组卷
|
10卷引用:上海市复旦大学附属中学2018-2019学年高三上学期期中数学试题
上海市复旦大学附属中学2018-2019学年高三上学期期中数学试题上海市复旦大学附属中学2019-2020学年高三上学期开学摸底数学试题湖南省长沙市明德中学2019-2020学年高一上学期期末数学试题上海市行知中学2020-2021学年高一上学期12月月考数学试题(已下线)4.2 指数函数-2021-2022学年高一数学尖子生同步培优题典(人教A版2019必修第一册)江苏省常州市第一中学2020-2021学年高一上学期期末数学试题(已下线)第8章 函数应用(培优卷)-【满分计划】2022-2023学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)期末测试卷02(培优卷)-【满分计划】2022-2023学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)专题07 函数恒成立等综合大题归类江苏省西安交通大学苏州附属中学2022-2023学年高一下学期开学考试数学试卷
5 . (1) 是以
是以 为定义域的减函数,且对于任意
为定义域的减函数,且对于任意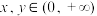 ,恒有
,恒有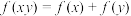 ,写出一个满足条件的函数
,写出一个满足条件的函数 的解析式;
的解析式;
(2) 是以
是以 为定义域的奇函数,且对于任意
为定义域的奇函数,且对于任意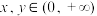 ,恒有
,恒有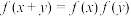 ,写出一个满足条件的函数
,写出一个满足条件的函数 的解析式;
的解析式;
(3) 都是以
都是以 为定义域的函数,写出一组满足下列条件的函数
为定义域的函数,写出一组满足下列条件的函数 的解析式,对于下列三组条件,只需选做一组,满分分别是①,②,③;若选择了多于一种的情形,则按照序号较小的解答计分.
的解析式,对于下列三组条件,只需选做一组,满分分别是①,②,③;若选择了多于一种的情形,则按照序号较小的解答计分.
①对于任意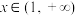 ,恒有
,恒有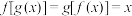 ;
;
②对于任意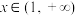 ,恒有
,恒有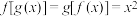 ;
;
③对于任意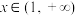 ,恒有
,恒有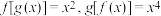 .
.
 是以
是以 为定义域的减函数,且对于任意
为定义域的减函数,且对于任意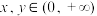 ,恒有
,恒有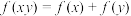 ,写出一个满足条件的函数
,写出一个满足条件的函数 的解析式;
的解析式;(2)
 是以
是以 为定义域的奇函数,且对于任意
为定义域的奇函数,且对于任意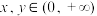 ,恒有
,恒有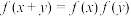 ,写出一个满足条件的函数
,写出一个满足条件的函数 的解析式;
的解析式;(3)
 都是以
都是以 为定义域的函数,写出一组满足下列条件的函数
为定义域的函数,写出一组满足下列条件的函数 的解析式,对于下列三组条件,只需选做一组,满分分别是①,②,③;若选择了多于一种的情形,则按照序号较小的解答计分.
的解析式,对于下列三组条件,只需选做一组,满分分别是①,②,③;若选择了多于一种的情形,则按照序号较小的解答计分.①对于任意
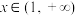 ,恒有
,恒有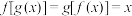 ;
;②对于任意
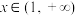 ,恒有
,恒有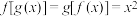 ;
;③对于任意
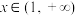 ,恒有
,恒有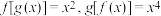 .
.
您最近一年使用:0次
6 . 已知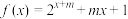 ,其中
,其中 是实常数.
是实常数.
(1)若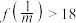 ,求
,求 的取值范围;
的取值范围;
(2)若 ,求证:函数
,求证:函数 的零点有且仅有一个;
的零点有且仅有一个;
(3)若 ,设函数
,设函数 的反函数为
的反函数为 ,若
,若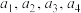 是公差
是公差 的等差数列且均在函数
的等差数列且均在函数 的值域中,求证:
的值域中,求证: .
.
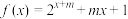 ,其中
,其中 是实常数.
是实常数.(1)若
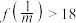 ,求
,求 的取值范围;
的取值范围;(2)若
 ,求证:函数
,求证:函数 的零点有且仅有一个;
的零点有且仅有一个;(3)若
 ,设函数
,设函数 的反函数为
的反函数为 ,若
,若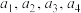 是公差
是公差 的等差数列且均在函数
的等差数列且均在函数 的值域中,求证:
的值域中,求证: .
.
您最近一年使用:0次



