解题方法
1 . 已知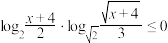 .
.
(1)求x的取值的集合A;
(2) 时,求函数
时,求函数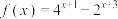 的值域;
的值域;
(3)设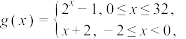 若
若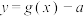 有两个零点
有两个零点 、
、 (
( ),求
),求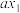 的取值范围.
的取值范围.
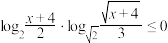 .
.(1)求x的取值的集合A;
(2)
 时,求函数
时,求函数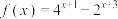 的值域;
的值域;(3)设
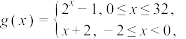 若
若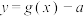 有两个零点
有两个零点 、
、 (
( ),求
),求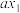 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
2 . 已知函数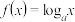 (
( ,且
,且 ),且
),且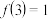 .
.
(1)求 的值,并写出函数
的值,并写出函数 的定义域;
的定义域;
(2)设函数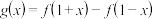 ,试判断
,试判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)若不等式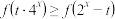 对任意
对任意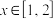 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
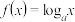 (
( ,且
,且 ),且
),且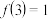 .
.(1)求
 的值,并写出函数
的值,并写出函数 的定义域;
的定义域;(2)设函数
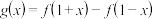 ,试判断
,试判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;(3)若不等式
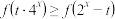 对任意
对任意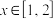 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-09-13更新
|
3148次组卷
|
17卷引用:湖南省地质中学2019-2020学年度高一上学期期中数学试题
湖南省地质中学2019-2020学年度高一上学期期中数学试题湖南省2016年普通高中学业水平考试数学试题2016年湖南省普通高中学业水平考试数学试题湖北省黄冈市黄梅国际育才高级中学2019-2020学年高一上学期12月月考数学试题(已下线)考点08 对数与对数函数-备战2021年高考数学(文)一轮复习考点一遍过(已下线)考点08 对数与对数函数-备战2021年高考数学(理)一轮复习考点一遍过(已下线)专题19+4.4对数函数(重点练)-2020-2021学年高一数学十分钟同步课堂专练(人教A版2019必修第一册)四川省江油中学2020-2021学年高三上学期开学考试数学(理)试题江苏省南通市四校(四星级学校)2020-2021学年高三上学期第一次联考数学试题江苏省南京大学附属中学2020-2021学年高三上学期第一次阶段检测数学试题(已下线)4.2.3 对数函数的性质与图像-2020-2021学年高一数学课时同步练(新人教B版必修第二册)陕西省咸阳市武功县普集高级中学2020-2021学年高三上学期第一次月考理科数学试题(已下线)专题4.4 指数函数、对数函数与幂函数(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教B版)江苏省盐城市响水中学2020-2021学年高一上学期期末数学试题(已下线)江苏省苏州三中2020-2021学年高一下学期3月期初数学试题(已下线)第8章 函数应用(基础卷)-【满分计划】2022-2023学年高一数学阶段性复习测试卷(苏教版2019必修第一册)(已下线)期末测试卷02(基础卷)-【满分计划】2022-2023学年高一数学阶段性复习测试卷(苏教版2019必修第一册)
名校
3 . 已知函数 .
.
(1)若函数 的最大值是
的最大值是 ,求
,求 的值;
的值;
(2)已知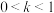 ,若存在两个不同的正数
,若存在两个不同的正数 ,当函数
,当函数 的定义域为
的定义域为 时,
时, 的值域为
的值域为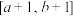 ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 的最大值是
的最大值是 ,求
,求 的值;
的值;(2)已知
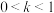 ,若存在两个不同的正数
,若存在两个不同的正数 ,当函数
,当函数 的定义域为
的定义域为 时,
时, 的值域为
的值域为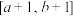 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-02-20更新
|
835次组卷
|
3卷引用:湖南省长沙市第一中学2019-2020学年高一上学期期末数学试题
13-14高三·全国·课后作业
名校
4 . 已知 图像关于
图像关于 轴对称.
轴对称.
(1)求 的值;
的值;
(2)若方程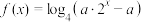 有且只有一个实根,求实数
有且只有一个实根,求实数 的取值范围.
的取值范围.
 图像关于
图像关于 轴对称.
轴对称.(1)求
 的值;
的值;(2)若方程
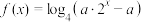 有且只有一个实根,求实数
有且只有一个实根,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-12-27更新
|
460次组卷
|
13卷引用:湖南省岳阳县第一中学2018届高三上学期第一次月考数学(文)试题
湖南省岳阳县第一中学2018届高三上学期第一次月考数学(文)试题(已下线)2014届上海交大附中高三数学理总复习二基本初等函数等练习卷(已下线)2013-2014学年江苏省无锡江阴市高二下学期期中考试文科数学试卷(已下线)2013-2014学年江苏省江阴祝塘中学五校高二下学期期中文科数学试卷2015-2016学年河北省邯郸市大名一中高二下第一次月考文科数学试卷河北省衡水市安平中学2017-2018学年高一上学期第二次月考数学试题1广东省深圳市第二实验学校2019-2020学年高一上学期期末数学试题内蒙古赤峰二中2020-2021学年高一上学期第二次月考数学(理)试题重庆市重庆第七中学2020-2021学年高一上学期12月月考数学试题湖南省怀化市2021-2022学年高一上学期期末数学试题广东省广州市第七中学2022-2023学年高一上学期期末(问卷)数学试题(已下线)第四章 幂函数、指数函数与对数函数(单元重点综合测试)-速记·巧练(沪教版2020必修第一册)(已下线)第四章 幂函数、指数函数与对数函数(压轴题专练)-速记·巧练(沪教版2020必修第一册)
名校
5 . 已知函数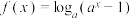 (
( ,
, )
)
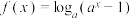 (
( ,
, )
)(1)当 时,求函数
时,求函数 的定义域;
的定义域;
(2)当 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;
(3)当 时,若不等式
时,若不等式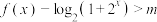 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2018-10-09更新
|
7189次组卷
|
20卷引用:江苏省南京师范大学附属中学2017-2018学年高一上学期期中考试数学试题
江苏省南京师范大学附属中学2017-2018学年高一上学期期中考试数学试题【校级联考】江苏省南京师大附中2017-2018学年高一第一学期期中考试数学试卷人教A版(2019) 必修第一册 突围者 第四章 第四节 对数函数江苏省扬州市邗江区2019-2020学年高一上学期期中数学试题浙江省金华市曙光学校2019-2020学年高二下学期返校测试数学试题河北省辛集中学2020-2021学年高一上学期第三次月考数学试题湖南省长沙市长沙县2021-2022学年高二下学期期末数学试题河北省邯郸市曲周县第一中学2020-2021学年高一下学期开学考试数学试题上海市华东师范大学第三附属中学2021-2022学年高二上学期第一次月考数学试题山西省怀仁市第一中学校云东校区2021-2022学年高一上学期第三次月考数学试题广东省韶关市武江区广东北江实验中学2020-2021学年高一下学期月考数学试题山西省怀仁市2021-2022学年高一上学期期末数学试题(已下线)专题01 《幂函数、指数函数和对数函数》中的典型题-2021-2022学年高一数学上册同步培优训练系列(苏教版2019)吉林省长春市协作校2022-2023学年高一上学期期中考试数学试题湖北省孝感市2022-2023学年高一下学期收心(开学)考试数学试题内蒙古呼伦贝尔市满洲里远方中学2022-2023学年高一下学期摸底考试数学试题北师大版(2019) 必修第一册 数学奇书 学业评价(三十二)对数函数 y=logax的图象和性质4.4.2 对数函数的图象与性质练习吉林省长春市汽车经济技术开发区第三中学2023-2024学年高一上学期期中考试数学试题(已下线)【第三练】4.4.1对数函数的概念+4.4.2对数函数的图象和性质 上好三课,做好三套题,高中数学素养晋级之路
名校
6 . 已知函数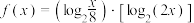 ,函数
,函数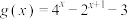 .
.
(1)求函数 的值域;
的值域;
(2)若不等式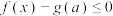 对任意实数
对任意实数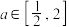 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
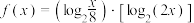 ,函数
,函数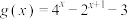 .
.(1)求函数
 的值域;
的值域;(2)若不等式
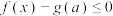 对任意实数
对任意实数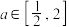 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2018-09-01更新
|
4813次组卷
|
17卷引用:【市级联考】辽宁省沈阳市2017-2018学年高一上学期期末数学试题
【市级联考】辽宁省沈阳市2017-2018学年高一上学期期末数学试题(已下线)2019年一轮复习讲练测【新课标版理】专题2.7 对数与对数函数(测)(已下线)2019年一轮复习讲练测【新课标版文】专题2.7 对数与对数函数(测)河北省邯郸市大名一中2019-2020学年度高一上学期实验班10月月考数学试题(已下线)4.4+对数函数-2020-2021学年新教材导学导练高中数学必修第一册(人教A版)湘鄂冀三省七校(益阳平高学校、长沙市平高中学等)2021-2022学年高一上学期12月联考数学试题(已下线)专题24 函数、不等式恒成立问题(测)-2021年高三数学二轮复习讲练测(新高考版)(已下线)2021年高三数学二轮复习讲练测之测案 专题十八 函数、不等式恒成立问题(文理通用)云南师范大学附属中学2021-2022年高一上学期期中考数学试题新疆石河子第二中学2021-2022学年高一上学期第二次月考数学试题北师大版(2019) 必修第一册 名校名师卷 第八单元 对数运算与对数函数A卷2023版 苏教版(2019) 必修第一册 名校名师卷 第九单元 对数函数 A卷2023版 湘教版(2019) 必修第一册 名师精选卷 第八单元 对数函数A卷江西省丰城中学2023届高三上学期第二次月考数学(理)试题江苏省镇江市句容碧桂园学校2022-2023学年高三上学期12月第二次月考模拟数学试题吉林省四平市第一高级中学2023-2024学年高一上学期第二次月考数学试题四川省德阳市绵竹中学2023-2024学年高一下学期第三次(6月)月考数学试题
7 . 已知集合A=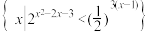 ,B={x|
,B={x|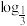 (9-x2)<
(9-x2)<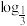 (6-2x)},又A∩B={x|x2+ax+b<0},求a+b的值.
(6-2x)},又A∩B={x|x2+ax+b<0},求a+b的值.
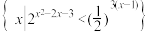 ,B={x|
,B={x|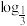 (9-x2)<
(9-x2)<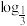 (6-2x)},又A∩B={x|x2+ax+b<0},求a+b的值.
(6-2x)},又A∩B={x|x2+ax+b<0},求a+b的值.
您最近一年使用:0次
2018-06-30更新
|
600次组卷
|
5卷引用:湖南省长沙市宁乡市2019-2020学年高一下学期期末数学试题
湖南省长沙市宁乡市2019-2020学年高一下学期期末数学试题【全国百强校】广东省广州市荔湾区实验中学2016-2017学年高一下学期期末考试数学试题(已下线)《2018-2019学年同步单元双基双测AB卷》必修一 月考二 第二章单元测试卷 B卷(已下线)第3章 章末检测-2018-2019版数学创新设计课堂讲义同步系列(苏教版必修5)福建省龙岩市连城县第一中学2019-2020学年高一上学期第一次月考数学试题
8 . 已知函数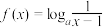 ,
,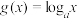
 且
且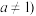 .
.
(1)当 时,设集合
时,设集合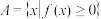 ,求集合
,求集合 ;
;
(2)在(1)的条件下,若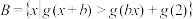 ,且满足
,且满足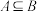 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若对任意的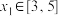 ,存在
,存在 ,使不等式
,使不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
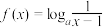 ,
,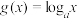
 且
且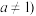 .
.(1)当
 时,设集合
时,设集合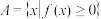 ,求集合
,求集合 ;
;(2)在(1)的条件下,若
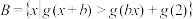 ,且满足
,且满足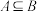 ,求实数
,求实数 的取值范围;
的取值范围;(3)若对任意的
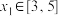 ,存在
,存在 ,使不等式
,使不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次



