1 . 已知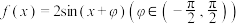 ,对任意
,对任意 都有
都有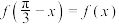 ,
,
(1)求 的值:
的值:
(2)若当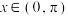 时方程
时方程 有唯一实根,求
有唯一实根,求 的范围.
的范围.
(3)已知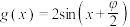 ,若对任意
,若对任意 都有
都有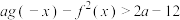 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
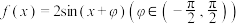 ,对任意
,对任意 都有
都有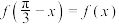 ,
,(1)求
 的值:
的值:(2)若当
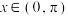 时方程
时方程 有唯一实根,求
有唯一实根,求 的范围.
的范围.(3)已知
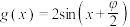 ,若对任意
,若对任意 都有
都有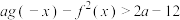 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2 . 若函数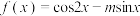 在
在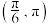 上有
上有 个零点,则
个零点,则 的取值范围是
的取值范围是__________ .
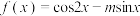 在
在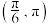 上有
上有 个零点,则
个零点,则 的取值范围是
的取值范围是
您最近一年使用:0次
2024-07-20更新
|
755次组卷
|
2卷引用:辽宁省辽阳市2023-2024学年高一下学期期末考试数学试卷
3 . 已知函数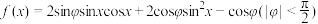 ,且
,且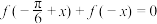 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(3)若函数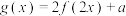 在区间
在区间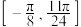 上恰有3个零点
上恰有3个零点 ,求a的取值范围和
,求a的取值范围和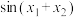 的值.
的值.
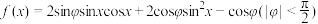 ,且
,且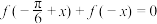 .
.(1)求函数
 的解析式;
的解析式;(2)求函数
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(3)若函数
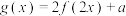 在区间
在区间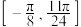 上恰有3个零点
上恰有3个零点 ,求a的取值范围和
,求a的取值范围和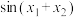 的值.
的值.
您最近一年使用:0次
名校
4 . 已知函数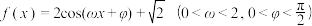 .
.
请在下面的三个条件中任选两个解答问题.
①函数 的图象过点
的图象过点 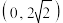 ;
;
②函数 的图象关于点
的图象关于点 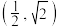 对称;
对称;
③函数 相邻对称轴与对称中心之间距离为1.
相邻对称轴与对称中心之间距离为1.
(1)求函数 的解析式;
的解析式;
(2)若 是函数
是函数  的零点,求
的零点,求 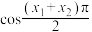 的值组成的集合;
的值组成的集合;
(3)当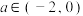 时,是否存在
时,是否存在 满足不等式
满足不等式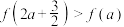 ?若存在,求出
?若存在,求出  的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
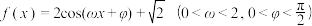 .
.请在下面的三个条件中任选两个解答问题.
①函数
 的图象过点
的图象过点 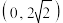 ;
;②函数
 的图象关于点
的图象关于点 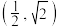 对称;
对称;③函数
 相邻对称轴与对称中心之间距离为1.
相邻对称轴与对称中心之间距离为1.(1)求函数
 的解析式;
的解析式;(2)若
 是函数
是函数  的零点,求
的零点,求 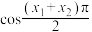 的值组成的集合;
的值组成的集合;(3)当
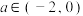 时,是否存在
时,是否存在 满足不等式
满足不等式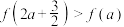 ?若存在,求出
?若存在,求出  的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
您最近一年使用:0次
2024-07-16更新
|
326次组卷
|
4卷引用:辽宁省名校联盟2023-2024学年高一下学期7月期末数学试题
辽宁省名校联盟2023-2024学年高一下学期7月期末数学试题辽宁省名校联盟2023-2024学年高一下学期7月期末考试数学试题(已下线)数学03(全国通用)-新高二上学期数学开学摸底考试卷海南省文昌中学2025届高三上学期第一次模拟考试数学试题
名校
解题方法
5 . 已知函数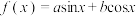 ,称非零向量
,称非零向量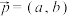 为
为 的“特征向量”,
的“特征向量”, 为
为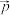 的“特征函数”.
的“特征函数”.
(1)设函数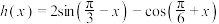 ,求函数
,求函数 的“特征向量”;
的“特征向量”;
(2)若函数 的“特征向量”为
的“特征向量”为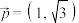 ,求当
,求当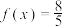 且
且 时
时 的值;
的值;
(3)若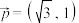 的“特征函数”为
的“特征函数”为 ,
,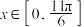 且方程
且方程 存在4个不相等的实数根,求实数a的取值范围.
存在4个不相等的实数根,求实数a的取值范围.
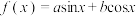 ,称非零向量
,称非零向量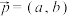 为
为 的“特征向量”,
的“特征向量”, 为
为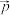 的“特征函数”.
的“特征函数”.(1)设函数
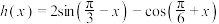 ,求函数
,求函数 的“特征向量”;
的“特征向量”;(2)若函数
 的“特征向量”为
的“特征向量”为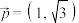 ,求当
,求当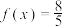 且
且 时
时 的值;
的值;(3)若
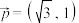 的“特征函数”为
的“特征函数”为 ,
,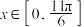 且方程
且方程 存在4个不相等的实数根,求实数a的取值范围.
存在4个不相等的实数根,求实数a的取值范围.
您最近一年使用:0次
2024-07-09更新
|
574次组卷
|
2卷引用:辽宁省抚顺市六校协作体2023-2024学年高一下学期期末考试数学试卷
解题方法
6 . 已知函数
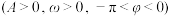 的部分图象如图所示.
的部分图象如图所示. 的解析式;
的解析式;
(2)当 时,关于x的方程
时,关于x的方程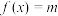 有两个不同的实根
有两个不同的实根 ,且
,且 ,求
,求 的最小值.
的最小值.

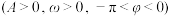 的部分图象如图所示.
的部分图象如图所示.
 的解析式;
的解析式;(2)当
 时,关于x的方程
时,关于x的方程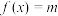 有两个不同的实根
有两个不同的实根 ,且
,且 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
7 . 已知函数 在
在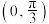 上有且仅有4个零点,则
上有且仅有4个零点,则 的值可能为( )
的值可能为( )
 在
在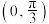 上有且仅有4个零点,则
上有且仅有4个零点,则 的值可能为( )
的值可能为( )| A.7 | B.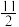 | C.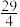 | D.6 |
您最近一年使用:0次
名校
8 . 定义非零向量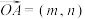 ,若函数解析式满足
,若函数解析式满足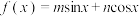 ,则称
,则称 为向量
为向量 的“
的“ 件生函数”,向量
件生函数”,向量 为函数
为函数 的“源向量”.
的“源向量”.
(1)已知向量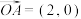 为函数
为函数 的“源向量”,若方程
的“源向量”,若方程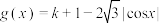 在
在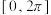 上有且仅有四个不相等的实数根,求实数k的取值范围;
上有且仅有四个不相等的实数根,求实数k的取值范围;
(2)已知点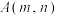 满足
满足 ,向量
,向量 的“
的“ 伴生函数”在
伴生函数”在 时取得最大值,当点A运动时,求
时取得最大值,当点A运动时,求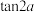 的取值范围;
的取值范围;
(3)已知向量 的“
的“ 件生函数”
件生函数” 在
在 时的取值为
时的取值为 .若
.若 中
中 ,
, ,点O为该三角形的外心,求
,点O为该三角形的外心,求 的最大值.
的最大值.
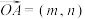 ,若函数解析式满足
,若函数解析式满足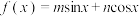 ,则称
,则称 为向量
为向量 的“
的“ 件生函数”,向量
件生函数”,向量 为函数
为函数 的“源向量”.
的“源向量”.(1)已知向量
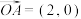 为函数
为函数 的“源向量”,若方程
的“源向量”,若方程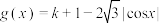 在
在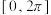 上有且仅有四个不相等的实数根,求实数k的取值范围;
上有且仅有四个不相等的实数根,求实数k的取值范围;(2)已知点
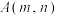 满足
满足 ,向量
,向量 的“
的“ 伴生函数”在
伴生函数”在 时取得最大值,当点A运动时,求
时取得最大值,当点A运动时,求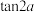 的取值范围;
的取值范围;(3)已知向量
 的“
的“ 件生函数”
件生函数” 在
在 时的取值为
时的取值为 .若
.若 中
中 ,
, ,点O为该三角形的外心,求
,点O为该三角形的外心,求 的最大值.
的最大值.
您最近一年使用:0次
2024-06-21更新
|
248次组卷
|
2卷引用:辽宁省大连市第八中学2023-2024学年高一下学期6月阶段测试数学试题
名校
9 . 已知函数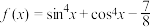 .
.
(1)若 ,函数
,函数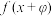 为偶函数,求
为偶函数,求 的最小值;
的最小值;
(2)若 在
在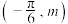 上恰有4个零点,求
上恰有4个零点,求 的取值范围;
的取值范围;
(3)若不等式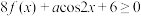 对任意的
对任意的 恒成立,求
恒成立,求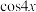 的取值范围.
的取值范围.
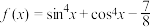 .
.(1)若
 ,函数
,函数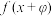 为偶函数,求
为偶函数,求 的最小值;
的最小值;(2)若
 在
在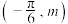 上恰有4个零点,求
上恰有4个零点,求 的取值范围;
的取值范围;(3)若不等式
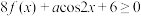 对任意的
对任意的 恒成立,求
恒成立,求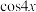 的取值范围.
的取值范围.
您最近一年使用:0次
名校
10 . 在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.在适当的直角坐标系下,某个简谐运动可以用函数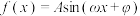 (
( ,
, ,
,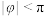 )的部分图象如图所示,则下列结论正确的是( )
)的部分图象如图所示,则下列结论正确的是( )
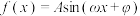 (
( ,
, ,
,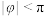 )的部分图象如图所示,则下列结论正确的是( )
)的部分图象如图所示,则下列结论正确的是( )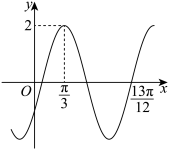
A. ,频率为 ,频率为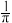 ,初相为 ,初相为 |
B.函数 的图象关于直线 的图象关于直线 对称 对称 |
C.函数 在 在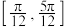 上的值域为 上的值域为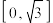 |
D.若 在 在 上恰有4个零点,则m的取值范围是 上恰有4个零点,则m的取值范围是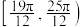 |
您最近一年使用:0次



