1 . 已知函数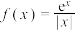 ,若函数
,若函数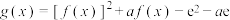 恰有5个不同的零点,则实数
恰有5个不同的零点,则实数 的取值范围是( )
的取值范围是( )
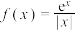 ,若函数
,若函数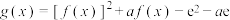 恰有5个不同的零点,则实数
恰有5个不同的零点,则实数 的取值范围是( )
的取值范围是( )A.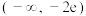 | B.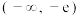 | C. | D. |
您最近一年使用:0次
2024-08-26更新
|
1359次组卷
|
6卷引用:辽宁省部分学校2024届高三抢分卷(二)数学试题
名校
解题方法
2 . 已知函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)若函数 在区间
在区间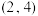 上不是单调函数,求
上不是单调函数,求 的取值范围;
的取值范围;
(3)若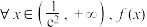 无零点,求
无零点,求 的取值范围.
的取值范围.
 .
.(1)当
 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;(2)若函数
 在区间
在区间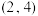 上不是单调函数,求
上不是单调函数,求 的取值范围;
的取值范围;(3)若
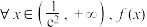 无零点,求
无零点,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-08-05更新
|
374次组卷
|
2卷引用:辽宁省七校协作体2024-2025学年高三上学期期初联考数学试题
3 . 已知函数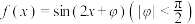 满足
满足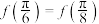 ,若
,若 在区间
在区间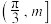 上恰有2个零点,则
上恰有2个零点,则 的取值范围为
的取值范围为____________ .(用区间表示)
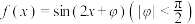 满足
满足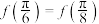 ,若
,若 在区间
在区间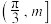 上恰有2个零点,则
上恰有2个零点,则 的取值范围为
的取值范围为
您最近一年使用:0次
4 . 已知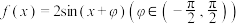 ,对任意
,对任意 都有
都有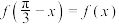 ,
,
(1)求 的值:
的值:
(2)若当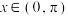 时方程
时方程 有唯一实根,求
有唯一实根,求 的范围.
的范围.
(3)已知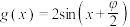 ,若对任意
,若对任意 都有
都有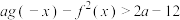 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
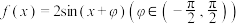 ,对任意
,对任意 都有
都有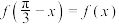 ,
,(1)求
 的值:
的值:(2)若当
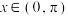 时方程
时方程 有唯一实根,求
有唯一实根,求 的范围.
的范围.(3)已知
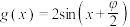 ,若对任意
,若对任意 都有
都有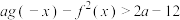 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
5 . 若函数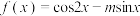 在
在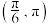 上有
上有 个零点,则
个零点,则 的取值范围是
的取值范围是__________ .
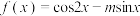 在
在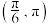 上有
上有 个零点,则
个零点,则 的取值范围是
的取值范围是
您最近一年使用:0次
2024-07-20更新
|
755次组卷
|
2卷引用:辽宁省辽阳市2023-2024学年高一下学期期末考试数学试卷
6 . 已知函数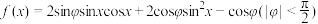 ,且
,且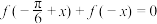 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(3)若函数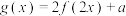 在区间
在区间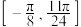 上恰有3个零点
上恰有3个零点 ,求a的取值范围和
,求a的取值范围和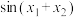 的值.
的值.
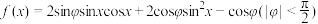 ,且
,且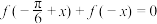 .
.(1)求函数
 的解析式;
的解析式;(2)求函数
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(3)若函数
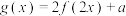 在区间
在区间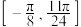 上恰有3个零点
上恰有3个零点 ,求a的取值范围和
,求a的取值范围和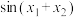 的值.
的值.
您最近一年使用:0次
名校
7 . 若函数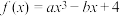 ,当
,当 时,函数
时,函数 有极值
有极值 .
.
(1)求函数的极值;
(2)若关于 的方程
的方程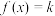 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
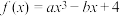 ,当
,当 时,函数
时,函数 有极值
有极值 .
.(1)求函数的极值;
(2)若关于
 的方程
的方程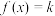 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-17更新
|
553次组卷
|
2卷引用:辽宁省沈阳市第二中学2023-2024学年高二下学期期末考试数学试卷
名校
8 . 已知函数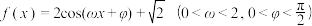 .
.
请在下面的三个条件中任选两个解答问题.
①函数 的图象过点
的图象过点 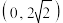 ;
;
②函数 的图象关于点
的图象关于点 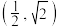 对称;
对称;
③函数 相邻对称轴与对称中心之间距离为1.
相邻对称轴与对称中心之间距离为1.
(1)求函数 的解析式;
的解析式;
(2)若 是函数
是函数  的零点,求
的零点,求 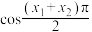 的值组成的集合;
的值组成的集合;
(3)当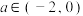 时,是否存在
时,是否存在 满足不等式
满足不等式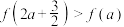 ?若存在,求出
?若存在,求出  的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
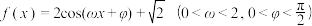 .
.请在下面的三个条件中任选两个解答问题.
①函数
 的图象过点
的图象过点 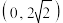 ;
;②函数
 的图象关于点
的图象关于点 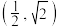 对称;
对称;③函数
 相邻对称轴与对称中心之间距离为1.
相邻对称轴与对称中心之间距离为1.(1)求函数
 的解析式;
的解析式;(2)若
 是函数
是函数  的零点,求
的零点,求 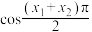 的值组成的集合;
的值组成的集合;(3)当
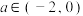 时,是否存在
时,是否存在 满足不等式
满足不等式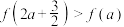 ?若存在,求出
?若存在,求出  的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
您最近一年使用:0次
2024-07-16更新
|
328次组卷
|
4卷引用:辽宁省名校联盟2023-2024学年高一下学期7月期末数学试题
辽宁省名校联盟2023-2024学年高一下学期7月期末数学试题辽宁省名校联盟2023-2024学年高一下学期7月期末考试数学试题(已下线)数学03(全国通用)-新高二上学期数学开学摸底考试卷海南省文昌中学2025届高三上学期第一次模拟考试数学试题
解题方法
9 . 已知函数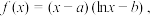 其中
其中 .
.
(1)若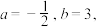 证明:当
证明:当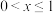 时,
时,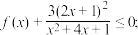
(2)若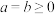 ,求证:
,求证: 有唯一极值点
有唯一极值点 ,且
,且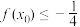 ;
;
(3)若 ,函数
,函数 有三个极值点
有三个极值点 证明:
证明: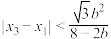 .
.
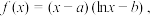 其中
其中 .
.(1)若
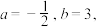 证明:当
证明:当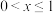 时,
时,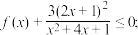
(2)若
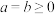 ,求证:
,求证: 有唯一极值点
有唯一极值点 ,且
,且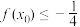 ;
;(3)若
 ,函数
,函数 有三个极值点
有三个极值点 证明:
证明: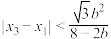 .
.
您最近一年使用:0次
名校
10 . 已知函数 ,下列选项中正确的是( )
,下列选项中正确的是( )
 ,下列选项中正确的是( )
,下列选项中正确的是( )A. 在 在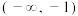 上单调递增,在 上单调递增,在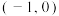 上单调递减 上单调递减 |
B. 有极大值 有极大值 |
C. 无最小值 无最小值 |
D.若函数 恰有6个零点,则实数 恰有6个零点,则实数 的取值范围是 的取值范围是 |
您最近一年使用:0次
2024-07-15更新
|
305次组卷
|
2卷引用:辽宁省锦州市2023-2024学年高二下学期期末考试数学试卷



