1 . 已知 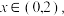
(1)比较 , x的大小, 并证明;
, x的大小, 并证明;
(2)求证: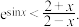
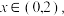
(1)比较
 , x的大小, 并证明;
, x的大小, 并证明;(2)求证:
您最近一年使用:0次
名校
2 . 已知 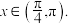
(1)将 ,
, ,
, ,
,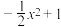 按由小到大排列,并证明;
按由小到大排列,并证明;
(2)令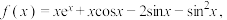 求证:
求证:  在
在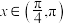 内无零点.
内无零点.
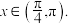
(1)将
 ,
, ,
, ,
,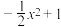 按由小到大排列,并证明;
按由小到大排列,并证明;(2)令
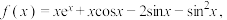 求证:
求证:  在
在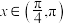 内无零点.
内无零点.
您最近一年使用:0次
2024-08-20更新
|
498次组卷
|
3卷引用:内蒙古赤峰市2024届高三下学期4.20模拟考试理科数学试题
3 . 已知函数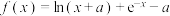 ,
,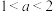 .
.
(1)求证: 有且仅有三零点.
有且仅有三零点.
(2)设 为最小的零点,证明:当
为最小的零点,证明:当 ,
,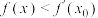 .
.
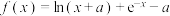 ,
,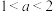 .
.(1)求证:
 有且仅有三零点.
有且仅有三零点.(2)设
 为最小的零点,证明:当
为最小的零点,证明:当 ,
,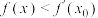 .
.
您最近一年使用:0次
名校
解题方法
4 . 已知函数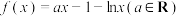 .
.
(1)若 ,求
,求 在区间
在区间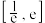 上的极值;
上的极值;
(2)讨论函数 的单调性;
的单调性;
(3)当 时,求证:
时,求证: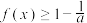 .
.
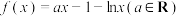 .
.(1)若
 ,求
,求 在区间
在区间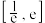 上的极值;
上的极值;(2)讨论函数
 的单调性;
的单调性;(3)当
 时,求证:
时,求证: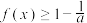 .
.
您最近一年使用:0次
名校
5 . 已知函数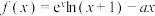 .
.
(1) 在
在 处切线斜率为2,求
处切线斜率为2,求 ;
;
(2)当 时,
时,
① ,证明:
,证明: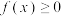 ;
;
②判断 的零点个数,并说明理由.
的零点个数,并说明理由.
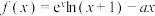 .
.(1)
 在
在 处切线斜率为2,求
处切线斜率为2,求 ;
;(2)当
 时,
时,①
 ,证明:
,证明: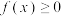 ;
;②判断
 的零点个数,并说明理由.
的零点个数,并说明理由.
您最近一年使用:0次
6 . 定义在区间 上的函数
上的函数 满足:若对任意
满足:若对任意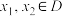 ,且
,且 ,都有
,都有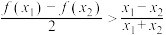 ,则称
,则称 是
是 上的“好函数”.
上的“好函数”.
(1)若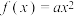 是
是 上的“好函数”,求
上的“好函数”,求 的取值范围.
的取值范围.
(2)(ⅰ)证明: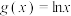 是
是 上的“好函数”.
上的“好函数”.
(ⅱ)设 ,证明:
,证明: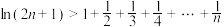 .
.
 上的函数
上的函数 满足:若对任意
满足:若对任意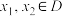 ,且
,且 ,都有
,都有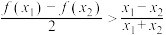 ,则称
,则称 是
是 上的“好函数”.
上的“好函数”.(1)若
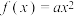 是
是 上的“好函数”,求
上的“好函数”,求 的取值范围.
的取值范围.(2)(ⅰ)证明:
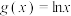 是
是 上的“好函数”.
上的“好函数”.(ⅱ)设
 ,证明:
,证明: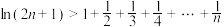 .
.
您最近一年使用:0次
2024-07-15更新
|
565次组卷
|
7卷引用:内蒙古自治区巴彦淖尔市2023-2024学年高二下学期7月期末考试数学试题
名校
7 . 对于函数 ,若实数
,若实数 满足
满足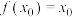 ,则
,则 称为
称为 的不动点.已知函数
的不动点.已知函数 .
.
(1)当 时,求证
时,求证 ;
;
(2)当 时,求函数
时,求函数 的不动点的个数;
的不动点的个数;
(3)设 ,证明
,证明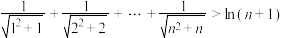 .
.
 ,若实数
,若实数 满足
满足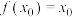 ,则
,则 称为
称为 的不动点.已知函数
的不动点.已知函数 .
.(1)当
 时,求证
时,求证 ;
;(2)当
 时,求函数
时,求函数 的不动点的个数;
的不动点的个数;(3)设
 ,证明
,证明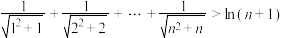 .
.
您最近一年使用:0次
2024-07-01更新
|
537次组卷
|
4卷引用:2024届内蒙古呼和浩特市高三第二次质量数据监测文数试卷
8 . 已知函数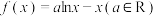 .
.
(1)若函数 在其定义域内有两个不同的零点,求实数
在其定义域内有两个不同的零点,求实数 的取值范围;
的取值范围;
(2)若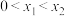 ,且
,且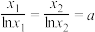 ,证明:
,证明: .
.
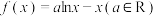 .
.(1)若函数
 在其定义域内有两个不同的零点,求实数
在其定义域内有两个不同的零点,求实数 的取值范围;
的取值范围;(2)若
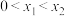 ,且
,且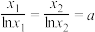 ,证明:
,证明: .
.
您最近一年使用:0次
名校
解题方法
9 . 已知函数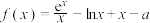 .
.
(1)当 ,求函数
,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(2)若 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)证明:若 有两个零点
有两个零点 ,则
,则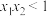 .
.
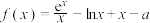 .
.(1)当
 ,求函数
,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)若
 恒成立,求a的取值范围;
恒成立,求a的取值范围;(3)证明:若
 有两个零点
有两个零点 ,则
,则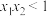 .
.
您最近一年使用:0次
2024-06-20更新
|
757次组卷
|
6卷引用:内蒙古自治区锡林郭勒盟2023-2024学年高二下学期末学业质量抽测数学试题
名校
解题方法
10 . 已知函数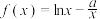 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)若 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)证明: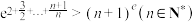 .
.
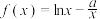 .
.(1)当
 时,求
时,求 的极值;
的极值;(2)若
 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)证明:
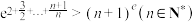 .
.
您最近一年使用:0次
2024-06-13更新
|
346次组卷
|
11卷引用:内蒙古自治区兴安盟乌兰浩特市第四中学2023-2024学年高二下学期期末考试数学试题
内蒙古自治区兴安盟乌兰浩特市第四中学2023-2024学年高二下学期期末考试数学试题四川省成都市郫都区2024届高三上学期阶段检测(三)文科数学试卷河北省邯郸市十校联考2023-2024学年高二下学期一调考试数学试题重庆市第十八中学2023-2024学年高二下学期中期学习能力摸底考试数学试题重庆市巴南育才实验中学校2023-2024学年高二下学期期中质量监测数学试题(已下线)专题5 导数与不等式恒成立问题【练】福建省泉州第一中学2023-2024学年高三下学期适应性测试数学试卷广东省广州市黄广中学2023-2024学年高二下学期期中考试数学试卷(已下线)专题19 导数综合(5大考向真题解读)陕西省榆林市神木市第四中学2024-2025学年高三上学期第二次检测考试数学试题陕西省榆林市府谷县府谷中学、府谷县第一中学2025届高三上学期第二次月考数学试题



