名校
1 . 记 为数列
为数列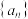 的前
的前 项和.若
项和.若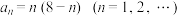 ,则( )
,则( )
 为数列
为数列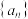 的前
的前 项和.若
项和.若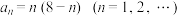 ,则( )
,则( )A.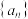 有最大项, 有最大项,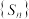 有最大项 有最大项 | B.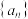 有最大项, 有最大项,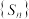 有最小项 有最小项 |
C.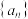 有最小项, 有最小项,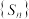 有最大项 有最大项 | D.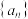 有最小项, 有最小项,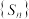 有最小项 有最小项 |
您最近一年使用:0次
2021-08-06更新
|
1434次组卷
|
12卷引用:陕西省咸阳市泾阳县2021-2022学年高二上学期期中文科数学试题
陕西省咸阳市泾阳县2021-2022学年高二上学期期中文科数学试题陕西省咸阳市泾阳县2021-2022学年高二上学期期中理科数学试题陕西省汉中市宁强县天津高级中学2021-2022学年高二上学期期中数学试题北京市西城区2020-2021学年高二下学期期末数学试题陕西省咸阳市武功县普集高中2021-2022学年高二上学期第三次月考文科数学试题北京师范大学第二附属中学2022届高三三模数学试题北京市育才学校2022届高三下学期仿真测试数学试题北京市北京理工大学附属中学2021-2022学年高二6月月考数学试题甘肃省庆阳市宁县第二中学2022-2023学年高二上学期第一次月考数学试题上海市2023届高三上学期二模暨秋考模拟1数学试题江西省宜春市宜丰县宜丰中学2023-2024学年高三上学期9月月考数学试题北京市怀柔区第一中学2023-2024学年高二下学期4月月考数学试题
名校
解题方法
2 . 已知数列 的前
的前 项和
项和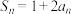 ,
, ,在等差数列
,在等差数列 中,
中, ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)求数列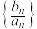 的最大值.
的最大值.
 的前
的前 项和
项和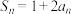 ,
, ,在等差数列
,在等差数列 中,
中, ,
, .
.(1)求
 的通项公式;
的通项公式;(2)求数列
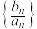 的最大值.
的最大值.
您最近一年使用:0次
2021-07-14更新
|
377次组卷
|
3卷引用:陕西省西安市高新一中2020-2021学年高一下学期期中数学试题
名校
解题方法
3 . 已知数列 的前
的前 项和为
项和为 ,且
,且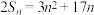 ,若
,若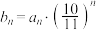 ,则数列
,则数列 的最大项为( )
的最大项为( )
 的前
的前 项和为
项和为 ,且
,且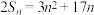 ,若
,若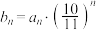 ,则数列
,则数列 的最大项为( )
的最大项为( )| A.第5项 | B.第6项 | C.第7项 | D.第8项 |
您最近一年使用:0次
2021-06-20更新
|
2308次组卷
|
13卷引用:河南省实验中学2021-2022学年高二上学期期中考试数学(理)试题
河南省实验中学2021-2022学年高二上学期期中考试数学(理)试题河南省正阳县高级中学2021届高三下学期第五次素质检测数学(理)试题(已下线)专题7.1 数列的概念与简单表示(讲)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题08 数列-2021年高考真题和模拟题数学(理)专项汇编(全国通用)(已下线)4.1数列(B 能力培优练)-2021-2022学年高二数学同步双培优检测(苏教版2019选择性必修第一册)(已下线)专题16数列的概念及其表示-2022年高三毕业班数学常考点归纳与变式演练(文理通用)福建省龙岩第一中学2021-2022学年高二上学期开学考试数学试题河南省豫南重点高中2021-2022学年高二上学期精英对抗赛理科数学试题(已下线)4.1 数列-2021-2022学年高二数学尖子生同步培优题典(苏教版2019选择性必修第一册)(已下线)专题15 盘点与数列有关的最值问题——备战2022年高考数学二轮复习常考点专题突破2023版 苏教版(2019) 选修第一册 名师精选卷 高考水平模拟性测试卷(二)重庆市第七中学校2023-2024学年高二上学期第四次月考数学试题(已下线)专题28 数列的概念与简单表示
4 . 已知数列 的前n项和为
的前n项和为 ,
,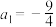 ,且
,且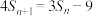 .
.
(1)求数列 的通项;
的通项;
(2)设数列 满足
满足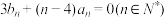 ,记
,记 的前n项和为
的前n项和为 ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的前n项和为
的前n项和为 ,
, ,且
,且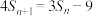 .
.(1)求数列
 的通项;
的通项;(2)设数列
 满足
满足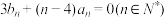 ,记
,记 的前n项和为
的前n项和为 ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-06-09更新
|
29862次组卷
|
77卷引用:河北省高碑店市崇德实验中学2023届高三上学期期中数学试题
河北省高碑店市崇德实验中学2023届高三上学期期中数学试题2021年浙江省高考数学试题(已下线)【新教材精创】第五章-复习与小结 -B提高练 四川省成都市玉林中学2020-2021学年高一下学期期末数学试题(已下线)专题7.11 数列大题(错位相减求和)-2022届高三数学一轮复习精讲精练(已下线)一轮复习大题专练31—数列(恒成立问题)-2022届高三数学一轮复习(已下线)2021年秋季高三数学开学摸底考试卷02(浙江专用)(已下线)第28讲 等比数列及其前n项和(讲)- 2022年高考数学一轮复习讲练测(课标全国版)(已下线)考点16 等比数列及其前n项和-备战2022年高考数学(理)一轮复习考点微专题(已下线)考点21 数列的概念与简单表示法-备战2022年高考数学(理)一轮复习考点帮(已下线)考点22 数列的综合应用-备战2022年高考数学一轮复习考点帮(浙江专用)(已下线)考点20 数列的概念与简单表示法-备战2022年高考数学(文)一轮复习考点帮(已下线)考向28 等比数列及其前n项和(重点)-备战2022年高考数学一轮复习考点微专题(新高考地区专用)(已下线)考向26 数列的概念与简单表示(重点)-备战2022年高考数学一轮复习考点微专题(新高考地区专用)(已下线)专题05 数列-十年(2012-2021)高考数学真题分项汇编(浙江专用)(已下线)专题09 数列-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)专题08 数列-2021年高考真题和模拟题数学(理)专项汇编(全国通用)(已下线)专题08 数列-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(已下线)考向15 等比数列-备战2022年高考数学一轮复习考点微专题(上海专用)(已下线)专题7.7 《数列与数学归纳法》单元测试卷 - 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题7.3 等比数列及其前n项和(练)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)2021年新高考浙江数学高考真题变式题17-22题山西省晋城市第一中学2021-2022学年高二上学期第七次学霸联赛数学试题(已下线)专题04数列求和及综合应用之讲案(文科)第一篇 热点、难点突破篇-《2022年高考文科数学二轮复习讲练测》(全国课标版)(已下线)专题08 数列的通项、求和及综合应用(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题二检测 数列(练)-2022年高考数学二轮复习讲练测(新教材地区专用)(已下线)专题04数列求和及综合应用 讲案 (理科)第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测》(全国课标版)(已下线)专题17 盘点数列与其它知识交汇问题——备战2022年高考数学二轮复习常考点专题突破(已下线)考点25 数列求和及其运用-备战2022年高考数学典型试题解读与变式(已下线)专题23 数列通项公式的求解策略-学会解题之高三数学万能解题模板【2022版】(已下线)专题24 数列求和的常见方法-学会解题之高三数学万能解题模板【2022版】河南省驻马店市第一高级中学2021-2022学年高二上学期10月月考数学(理)试题人教B版(2019) 选修第三册 必杀技 第五章 素养检测人教B版(2019) 选修第三册 一蹴而就 第五章 高考真题(已下线)技巧03 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)4.3等比数列B卷(已下线)思想04 化归与转化思想(讲)--第三篇 思想方法篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)专题24 真题优选重组第一卷-备战2022年高考数学冲刺横向强化精练精讲(新高考专用)湖南师范大学附属中学2022届高三下学期一模数学试题(已下线)押新高考第18题 数列-备战2022年高考数学临考题号押题(新高考专用)(已下线)解密08 数列(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)(已下线)查补易混易错点04 数列-【查漏补缺】2022年高考数学三轮冲刺过关(新高考专用)(已下线)押全国卷(文科)第17题 解三角形与数列-备战2022年高考数学(文)临考题号押题(全国卷)(已下线)2022年高考考前20天终极冲刺攻略(三)【数学】(新高考地区专用)(5月31日)(已下线)押全国卷(理科)第17题 解三角形与数列-备战2022年高考数学(理)临考题号押题(全国卷)广东省佛山市南海区狮山石门高级中学2021-2022学年高二下学期第二次大测数学试题(已下线)6.4 求和方法(精讲)2023版 湘教版(2019) 选修第一册 过关斩将 第1章 1.3.3 等比数列的前n项的和(已下线)第01讲 数列的概念与简单表示法(练)(已下线)专题07 数列(测)(已下线)专题6-1 数列递推与通项公式22种归类-3(已下线)专题6-2 数列求和归类-2广东省中山市小榄中学2023届高三上学期第三次月考数学试题(已下线)专题5 数列 第2讲 数列通项与求和河南省三门峡市2022-2023学年高三上学期第一次大练习(期末)数学(理科)试题(已下线)重组卷04(已下线)拓展五:近五年数列高考真题分类汇编(2)甘肃省天水市麦积区第二中学2023-2024学年高二上学期10月月考数学试题广东省深圳市云顶学校2024届高三上学期8月质量检测数学试题(已下线)第04讲 数列的通项公式(练习)-2(已下线)考点12 数列中的不等关系 2024届高考数学考点总动员(已下线)专题04 数列(4)(已下线)重难点03:数列近3年高考真题赏析-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)专题10 数列不等式的放缩问题 (7大核心考点)(讲义)(已下线)专题05 数列 第三讲 数列与不等关系(解密讲义)(已下线)专题05 数列 第二讲 数列的求和(解密讲义)(已下线)专题05 数列 第一讲 数列的递推关系(解密讲义)黑龙江省齐齐哈尔市第八中学校2023-2024学年高二下学期3月月考数学试题江西省宜春市丰城市第九中学2023-2024学年高二下学期第一次月考数学试题吉林省四平市第一高级中学2023-2024学年高二下学期第一次月考数学试题(已下线)专题21 数列解答题(文科)-3(已下线)专题21 数列解答题(理科)-4(已下线)模块三 失分陷阱4 模块融合题找不准解题方法湖南省吉首市2024届高三下学期5月模拟考试数学试题(已下线)第03讲 等比数列及其前n项和(九大题型)(练习)(已下线)4.3.2等比数列的前n项和公式 第三课 知识扩展延伸江苏省苏州三中2024-2025学年高二上学期10月月考数学试题
名校
解题方法
5 . 已知等比数列 中,
中,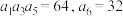 ,若
,若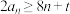 恒成立,则实数
恒成立,则实数 的最大值为( )
的最大值为( )
 中,
中,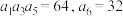 ,若
,若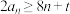 恒成立,则实数
恒成立,则实数 的最大值为( )
的最大值为( )A.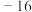 | B.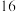 | C. | D. |
您最近一年使用:0次
2021-05-10更新
|
1637次组卷
|
10卷引用:宁夏石嘴山市平罗中学2022届高三上学期期中考试数学(理)试题
宁夏石嘴山市平罗中学2022届高三上学期期中考试数学(理)试题数学-学科网2021年高三5月大联考(山东卷)数学-学科网2021年高三5月大联考(广东卷)宁夏石嘴山市第三中学2021届高三四模数学(理)试题(已下线)专题7.4 等比数列-2022届高三数学一轮复习精讲精练(已下线)考点16 等比数列及其前n项和-备战2022年高考数学(理)一轮复习考点微专题(已下线)考点21 数列的概念与简单表示法-备战2022年高考数学(理)一轮复习考点帮甘肃省武威市武威六中2020-2021学年高三第十次诊断考试数学(理)试题陕西省渭南市集才中学老城分校2021-2022学年高三上学期期末理科数学试题(已下线)专题 12等比数列性质及应用归类(3)
名校
解题方法
6 . 已知数列{an}的通项公式 ,前n项和为Sn,若m>n,则Sm﹣Sn的最大值是( )
,前n项和为Sn,若m>n,则Sm﹣Sn的最大值是( )
 ,前n项和为Sn,若m>n,则Sm﹣Sn的最大值是( )
,前n项和为Sn,若m>n,则Sm﹣Sn的最大值是( )| A.5 | B.10 | C.15 | D.20 |
您最近一年使用:0次
2021-04-22更新
|
1054次组卷
|
13卷引用:四川省成都市双流区成都棠湖外国语学校2020-2021学年高二下学期期中数学理科试题
四川省成都市双流区成都棠湖外国语学校2020-2021学年高二下学期期中数学理科试题宁夏银川市一中2018-2019学年高一下学期期末数学试题河北省石家庄市第二中学2019-2020学年高二上学期开学考试数学试题河北省张家口市宣化区宣化第一中学2020-2021学年高二上学期期初数学试题(已下线)第04章 数列(B卷提高卷)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教A版)安徽省蚌埠市第二中学2021届高三下学期高考最后一模理科数学试题(已下线)专题01 数列【专项训练】-2020-2021学年高二数学下学期期末专项复习(新人教B版2019)安徽省蚌埠市第二中学2021届高三下学期高考最后一模文科数学试题(已下线)4.1数列的概念-【优质课堂】2021-2022学年高二数学同步课时优练测(人教A版2019选择性必修第二册)(已下线)4.1 数列-2021-2022学年高二数学链接教材精准变式练(苏教版2019选择性必修第一册)(已下线)4.1 数列(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)江苏省扬州中学2021-2022学年高三下学期3月月考数学试题吉林省松原市前郭尔罗斯蒙古族自治县第五中学2020-2021学年高三5月月考数学试题
7 . 已知数列{an}是递增的等比数列,前3项和为13,且a1+3,3a2,a3+5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{bn}的首项b1=1,其前n项和为Sn,且 ,若数列{cn}满足cn=anbn,{cn}的前n项和为Tn,求Tn的最小值.
在如下三个条件中任意选择一个,填入上面横线处,并根据题意解决问题.
①3Sn+bn=4;②bn=bn-1+2(n≥2);③5bn=-bn-1(n≥2).
(1)求数列{an}的通项公式;
(2)数列{bn}的首项b1=1,其前n项和为Sn,且 ,若数列{cn}满足cn=anbn,{cn}的前n项和为Tn,求Tn的最小值.
在如下三个条件中任意选择一个,填入上面横线处,并根据题意解决问题.
①3Sn+bn=4;②bn=bn-1+2(n≥2);③5bn=-bn-1(n≥2).
您最近一年使用:0次
2021-02-26更新
|
739次组卷
|
9卷引用:江苏省南通市启东市2020-2021学年高二上学期期中数学试题
江苏省南通市启东市2020-2021学年高二上学期期中数学试题(已下线)练习5+数列求和-2020-2021学年【补习教材·寒假作业】高二数学(苏教版)(已下线)高二上学期期末综合测试二+(B卷提升卷)-2020-2021学年高二数学上学期同步单元AB卷(苏教版,新课改地区专用)(已下线)思想05 第三篇 思想方法(测试卷)-2021年高考二轮复习讲练测(浙江专用)(已下线)押第20题数列-备战2021年高考数学临考题号押题(浙江专用)江苏省南京市第二十九中学2020-2021学年高二下学期3月月考数学试题江苏省南京市秦淮中学2020-2021学年高二下学期第一次月考数学试题(已下线)专题2.4 数列-结构不良型-2021年高考数学解答题挑战满分专项训练(新高考地区专用)江苏省南京市第二十九中学2020-2021学年高二上学期期末数学试题
8 . 在等差数列 中,
中,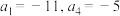 .记
.记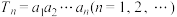 ,则数列
,则数列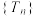 ( )
( )
 中,
中,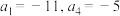 .记
.记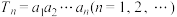 ,则数列
,则数列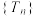 ( )
( )| A.有最大项,有最小项 | B.有最大项,无最小项 |
| C.无最大项,有最小项 | D.无最大项,无最小项 |
您最近一年使用:0次
2021-02-25更新
|
892次组卷
|
5卷引用:北京市第九中学2022-2023学年高二下学期期中考试数学试题
北京市第九中学2022-2023学年高二下学期期中考试数学试题江西省上饶市2021届高三年级第一次联考数学(文)试题(已下线)第四章 数列(基础测评卷)-2020-2021学年高二数学单元复习(人教A版2019选择性必修第二册)(已下线)解密10 等差数列、等比数列(分层训练)-【高频考点解密】2021年高考数学(文)二轮复习讲义+分层训练北京高二专题03数列(第二部分)
解题方法
9 . 已知数列 中,
中, ,
, ,数列
,数列 中,
中, ,
, .
.
(1)求 和
和 的通项公式;
的通项公式;
(2)若数列 求数列
求数列 的前
的前 项和
项和 ,并求使得
,并求使得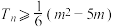 恒成立的最大正整数
恒成立的最大正整数 的值.
的值.
 中,
中, ,
, ,数列
,数列 中,
中, ,
, .
.(1)求
 和
和 的通项公式;
的通项公式;(2)若数列
 求数列
求数列 的前
的前 项和
项和 ,并求使得
,并求使得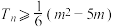 恒成立的最大正整数
恒成立的最大正整数 的值.
的值.
您最近一年使用:0次
2021-01-29更新
|
216次组卷
|
2卷引用:江西省部分学校2024届高三上学期期中数学试题
10 . 已知数列 中,
中, ,
,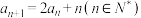 .
.
(1)令 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(2)令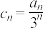 ,当
,当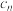 取得最大值时,求
取得最大值时,求 的值.
的值.
 中,
中, ,
,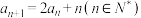 .
.(1)令
 ,求证:数列
,求证:数列 是等比数列;
是等比数列;(2)令
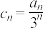 ,当
,当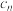 取得最大值时,求
取得最大值时,求 的值.
的值.
您最近一年使用:0次
2020-12-29更新
|
1867次组卷
|
19卷引用:浙江省宁波市北仑中学2020-2021学年高一(1班)上学期期中数学试题
浙江省宁波市北仑中学2020-2021学年高一(1班)上学期期中数学试题江苏省南京市联合体学校2018届高三调研测试数学(理)试题(已下线)《2018届优等生百日闯关系列》【江苏版】专题二 第六关 以新定义数列为背景的解答题【市级联考】浙江省温州九校2019届高三第一次联考数学试题(已下线)第03讲 等比数列及其前n项和 (练)-《2020年高考一轮复习讲练测》(已下线)第04讲 数列求和(练)-《2020年高考一轮复习讲练测》(浙江版)2019年浙江省新高考优化提升卷(三)(已下线)专题06 数列中的最值问题(第二篇)-备战2020年高考数学大题精做之解答题题型全覆盖(已下线)专题7.3 等比数列及其前n项和(练)-2021年新高考数学一轮复习讲练测(已下线)专题7.3 等比数列及其前n项和(精练)-2021年新高考数学一轮复习学与练(已下线)专题7.4 数列求和(练)-2021年新高考数学一轮复习讲练测(已下线)专题01 利用构造或猜想,解决数列递推问题 (第三篇)-2020高考数学压轴题命题区间探究与突破(已下线)专题7.4 数列求和(练)- 2022年高考数学一轮复习讲练测(新教材新高考)(已下线)专题7.3 等比数列及其前n项和(练)- 2022年高考数学一轮复习讲练测(新教材新高考)湖南省长沙市雅礼中学2024届高三上学期月考(一)数学试题江西省宜春市宜丰中学创新部2024届高三上学期第一次(10月)月考数学试题湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题(已下线)河南省信阳市信阳高级中学2024届高三一模数学试题河南省信阳高级中学2024届高三上学期月考(五)数学试题



