名校
1 . 如图,在直三棱柱 中,△ABC是以BC为斜边的等腰直角三角形,
中,△ABC是以BC为斜边的等腰直角三角形, ,点D,E分别为棱BC,
,点D,E分别为棱BC, 上的中点.
上的中点.

(1)求证:AD//平面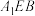 ;
;
(2)若二面角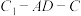 的大小为
的大小为 ,求实数t的值.
,求实数t的值.
 中,△ABC是以BC为斜边的等腰直角三角形,
中,△ABC是以BC为斜边的等腰直角三角形, ,点D,E分别为棱BC,
,点D,E分别为棱BC, 上的中点.
上的中点.
(1)求证:AD//平面
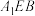 ;
;(2)若二面角
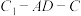 的大小为
的大小为 ,求实数t的值.
,求实数t的值.
您最近一年使用:0次
2022-10-30更新
|
390次组卷
|
2卷引用:贵州省贵阳第一中学2023届高三上学期高考适应性月考卷(二)数学(理)试题
名校
解题方法
2 . 如图,在四棱锥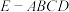 中,
中, ,
,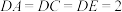 ,
,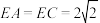 ,
, 是
是 的中点.
的中点.
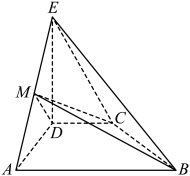
(1)证明:平面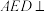 平面
平面 ;
;
(2)若平面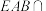 平面
平面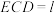 ,且
,且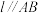 ,三棱锥
,三棱锥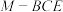 的体积为1,求
的体积为1,求 的长.
的长.
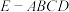 中,
中, ,
,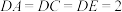 ,
,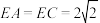 ,
, 是
是 的中点.
的中点.
(1)证明:平面
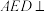 平面
平面 ;
;(2)若平面
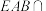 平面
平面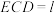 ,且
,且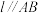 ,三棱锥
,三棱锥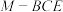 的体积为1,求
的体积为1,求 的长.
的长.
您最近一年使用:0次
2022-10-30更新
|
483次组卷
|
2卷引用:贵州省贵阳第一中学2023届高三上学期高考适应性月考卷(一)数学(文)试题
名校
3 . 设 ,
, 为两条不同的直线,
为两条不同的直线, ,
, 为两个不同的平面,则下列结论正确的是( )
为两个不同的平面,则下列结论正确的是( )
 ,
, 为两条不同的直线,
为两条不同的直线, ,
, 为两个不同的平面,则下列结论正确的是( )
为两个不同的平面,则下列结论正确的是( )A.若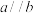 , ,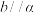 ,则 ,则 | B.若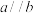 , , , ,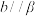 ,则 ,则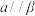 |
C.若 , , , ,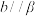 ,则 ,则 | D.若 , ,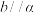 ,则 ,则 |
您最近一年使用:0次
2022-07-17更新
|
753次组卷
|
4卷引用:贵州省贵阳第一中学2023届高三上学期高考适应性月考卷(二)数学(理)试题
名校
4 . 如图,四棱锥 中,平面
中,平面 平面
平面 ,
,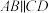 ,
, ,
, ,
, ,
,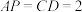 ,
,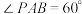 .
. 是
是 中点,
中点, 是
是 上一点.
上一点.

(1)是否存在点 使得
使得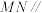 平面
平面 ,若存在求
,若存在求 的长.若不存在,请说明理由;
的长.若不存在,请说明理由;
(2)二面角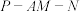 的余弦值为
的余弦值为 ,求
,求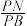 的值.
的值.
 中,平面
中,平面 平面
平面 ,
,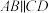 ,
, ,
, ,
, ,
,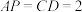 ,
,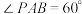 .
. 是
是 中点,
中点, 是
是 上一点.
上一点.
(1)是否存在点
 使得
使得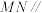 平面
平面 ,若存在求
,若存在求 的长.若不存在,请说明理由;
的长.若不存在,请说明理由;(2)二面角
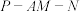 的余弦值为
的余弦值为 ,求
,求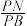 的值.
的值.
您最近一年使用:0次
2022-06-07更新
|
1159次组卷
|
5卷引用:贵阳第一中学2022届5月高三高考适应性月考卷(八)数学(理)试题
贵阳第一中学2022届5月高三高考适应性月考卷(八)数学(理)试题(已下线)专题32 空间向量及其应用-5重庆市实验中学2021-2022学年高二下学期期末复习(二)数学试题(已下线)7.3 空间角(精练)(已下线)第五章 破解立体几何开放探究问题 专题二 立体几何开放题的解法 微点3 立体几何开放题的解法综合训练【培优版】
解题方法
5 . 如图,在四棱锥 中,
中, ,
,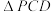 是边长为
是边长为 的正三角形,平面
的正三角形,平面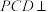 平面
平面 ,
,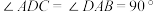 ,点
,点 ,
, ,
, 分别是线段
分别是线段 ,
, ,
, 的中点.
的中点.
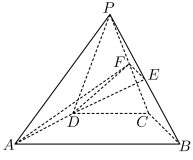
(1)求证:点 在平面
在平面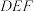 内;
内;
(2)若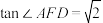 ,求三棱锥
,求三棱锥 的体积.
的体积.
 中,
中, ,
,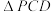 是边长为
是边长为 的正三角形,平面
的正三角形,平面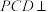 平面
平面 ,
,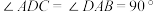 ,点
,点 ,
, ,
, 分别是线段
分别是线段 ,
, ,
, 的中点.
的中点.
(1)求证:点
 在平面
在平面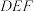 内;
内;(2)若
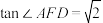 ,求三棱锥
,求三棱锥 的体积.
的体积.
您最近一年使用:0次
解题方法
6 . 在棱柱 中,底面
中,底面 为平行四边形,
为平行四边形, 为线段
为线段 上一动点.
上一动点.

(1)证明: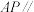 平面
平面 ;
;
(2)若 平面
平面 ,
,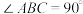 ,
,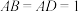 ,
,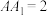 ,且
,且 为线段
为线段 的中点,求点
的中点,求点 到平面
到平面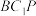 的距离.
的距离.
 中,底面
中,底面 为平行四边形,
为平行四边形, 为线段
为线段 上一动点.
上一动点.
(1)证明:
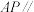 平面
平面 ;
;(2)若
 平面
平面 ,
,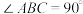 ,
,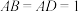 ,
,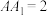 ,且
,且 为线段
为线段 的中点,求点
的中点,求点 到平面
到平面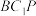 的距离.
的距离.
您最近一年使用:0次
解题方法
7 . 如图,在直三棱柱 中,
中,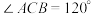 ,
,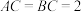 ,
, ,点
,点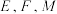 分别为
分别为 的中点.
的中点.

(1)判断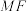 与平面
与平面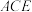 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求二面角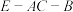 的正弦值.
的正弦值.
 中,
中,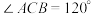 ,
,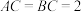 ,
, ,点
,点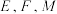 分别为
分别为 的中点.
的中点.
(1)判断
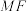 与平面
与平面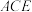 的位置关系,并说明理由;
的位置关系,并说明理由;(2)求二面角
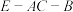 的正弦值.
的正弦值.
您最近一年使用:0次
8 . 如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 为菱形,
为菱形,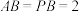 ,
, ,点
,点 分别是
分别是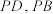 的中点.
的中点.
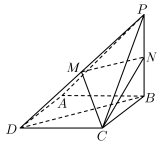
(1)记平面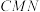 与平面
与平面 的交线为
的交线为 ,试判断直线
,试判断直线 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)求二面角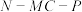 的正弦值.
的正弦值.
 中,
中, 平面
平面 ,底面
,底面 为菱形,
为菱形,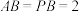 ,
, ,点
,点 分别是
分别是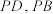 的中点.
的中点.
(1)记平面
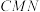 与平面
与平面 的交线为
的交线为 ,试判断直线
,试判断直线 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;(2)求二面角
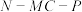 的正弦值.
的正弦值.
您最近一年使用:0次
解题方法
9 . 如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 为菱形,
为菱形,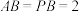 ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
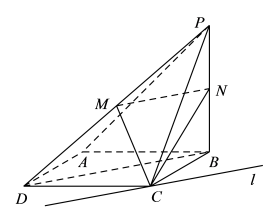
(1)记平面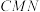 与平面
与平面 的交线为
的交线为 ,试判断直线
,试判断直线 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)求点 到平面
到平面 的距离.
的距离.
 中,
中, 平面
平面 ,底面
,底面 为菱形,
为菱形,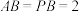 ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)记平面
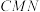 与平面
与平面 的交线为
的交线为 ,试判断直线
,试判断直线 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2022-03-25更新
|
303次组卷
|
2卷引用:贵州省贵阳市五校(贵州省实验中学、贵阳二中、贵阳八中、贵阳九中、贵阳民中)2022届高三年级联合考试(六)数学(文)试题
解题方法
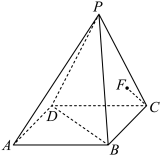
10 . 如图,在四棱锥 中,
中,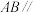 平面
平面 ,平面
,平面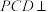 底面
底面 ,且
,且 ,
,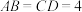 ,
, .
.
(1)证明: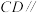 平面
平面 .
.
(2)若 为侧面
为侧面 内到
内到 距离为1的一点,且
距离为1的一点,且 ,
, ,求
,求 到
到 的距离.
的距离.
 中,
中,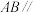 平面
平面 ,平面
,平面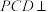 底面
底面 ,且
,且 ,
,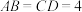 ,
, .
.
(1)证明:
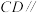 平面
平面 .
.(2)若
 为侧面
为侧面 内到
内到 距离为1的一点,且
距离为1的一点,且 ,
, ,求
,求 到
到 的距离.
的距离.
您最近一年使用:0次



