名校
解题方法
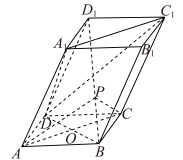
1 . 如图,平行六面体 中,点P在对角线
中,点P在对角线 上,
上,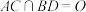 ,平面
,平面 平面
平面 .
. 三点共线;
三点共线;
(2)若四边形 是边长为2的菱形,
是边长为2的菱形,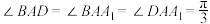 ,
, ,求二面角
,求二面角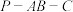 大小的余弦值.
大小的余弦值.
 中,点P在对角线
中,点P在对角线 上,
上,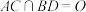 ,平面
,平面 平面
平面 .
.
 三点共线;
三点共线;(2)若四边形
 是边长为2的菱形,
是边长为2的菱形,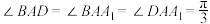 ,
, ,求二面角
,求二面角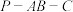 大小的余弦值.
大小的余弦值.
您最近一年使用:0次
2023-04-16更新
|
3068次组卷
|
5卷引用:湖北省武汉市华中师范大学第一附属中学2023届高三高考前素养数学试题
解题方法
2 . 如图,四棱柱 的底面为菱形,
的底面为菱形, 为
为 中点,
中点, 为
为 中点,
中点, 为
为 中点.
中点.
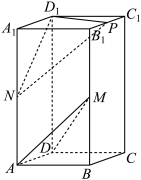
(1)证明:直线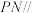 平面
平面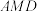 ;
;
(2)若 平面
平面 ,
, ,
,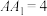 ,
, ,求平面
,求平面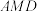 与平面
与平面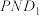 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
 的底面为菱形,
的底面为菱形, 为
为 中点,
中点, 为
为 中点,
中点, 为
为 中点.
中点.
(1)证明:直线
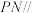 平面
平面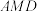 ;
;(2)若
 平面
平面 ,
, ,
,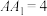 ,
, ,求平面
,求平面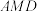 与平面
与平面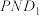 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
您最近一年使用:0次
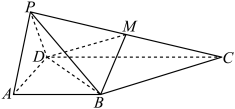
3 . 如图,四棱锥 中,
中,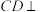 平面
平面 ,
, ,
, ,
,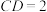 ,
, 为棱
为棱 上一点.
上一点.
(1)若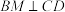 ,证明:
,证明: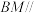 平面
平面 ;
;
(2)若 ,且
,且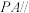 平面
平面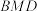 ,求直线
,求直线 与平面
与平面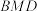 所成角的正弦值.
所成角的正弦值.
 中,
中,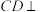 平面
平面 ,
, ,
, ,
,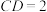 ,
, 为棱
为棱 上一点.
上一点.
(1)若
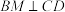 ,证明:
,证明: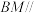 平面
平面 ;
;(2)若
 ,且
,且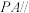 平面
平面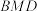 ,求直线
,求直线 与平面
与平面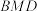 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
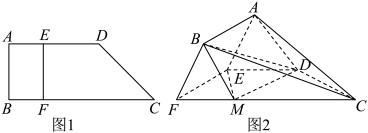
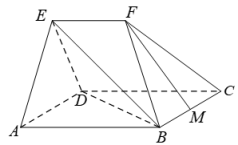
4 . 如图1,直角梯形 中,
中,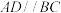 ,
, ,E、F分别是
,E、F分别是 和
和 上的点,且
上的点,且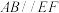 ,
,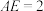 ,
,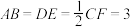 ,沿
,沿 将四边形
将四边形 折起,如图2,使
折起,如图2,使 与
与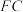 所成的角为60°.
所成的角为60°.
(1)求证: 平面
平面 ;
;
(2)M为 上的点,
上的点,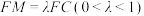 ,若二面角
,若二面角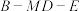 的余弦值为
的余弦值为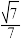 ,求
,求 的值.
的值.
 中,
中,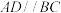 ,
, ,E、F分别是
,E、F分别是 和
和 上的点,且
上的点,且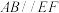 ,
,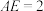 ,
,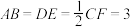 ,沿
,沿 将四边形
将四边形 折起,如图2,使
折起,如图2,使 与
与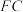 所成的角为60°.
所成的角为60°.
(1)求证:
 平面
平面 ;
;(2)M为
 上的点,
上的点,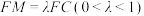 ,若二面角
,若二面角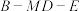 的余弦值为
的余弦值为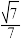 ,求
,求 的值.
的值.
您最近一年使用:0次
5 . 如图,在长方体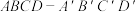 中,
中, ,
, 是
是 上一点,
上一点,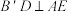 ,设
,设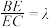 .
.
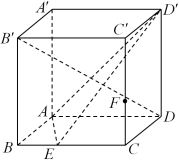
(1)求 的值;
的值;
(2)设 ,
,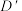 ,
, 的截面交
的截面交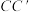 于
于 .
.
①求证: ;
;
②设 ,截面
,截面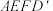 将长方体分成两部分,记含
将长方体分成两部分,记含 点部分体积为
点部分体积为 ,求
,求 .
.
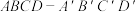 中,
中, ,
, 是
是 上一点,
上一点,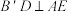 ,设
,设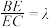 .
.
(1)求
 的值;
的值;(2)设
 ,
,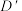 ,
, 的截面交
的截面交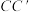 于
于 .
.①求证:
 ;
;②设
 ,截面
,截面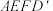 将长方体分成两部分,记含
将长方体分成两部分,记含 点部分体积为
点部分体积为 ,求
,求 .
.
您最近一年使用:0次
名校
6 . 如图,在四棱锥S-ABCD中,底面ABCD是菱形, ,
, 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
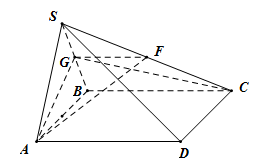
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD, ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
 ,
, 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,
 ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
您最近一年使用:0次
2020-03-09更新
|
512次组卷
|
5卷引用:2020届湖北省武汉市高三下学期2月调考仿真模拟数学文科试题
名校
7 . 如图1,矩形 中,
中, ,M是
,M是 边上异于端点的动点,
边上异于端点的动点,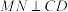 于点N,将矩形
于点N,将矩形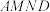 沿
沿 折叠至
折叠至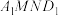 处,使面
处,使面 面
面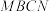 (如图2).点E,F满足
(如图2).点E,F满足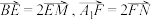 .
.

(1)证明: 面
面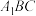 ;
;
(2)设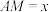 ,当x为何值时,四面体
,当x为何值时,四面体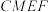 的体积最大,并求出最大值.
的体积最大,并求出最大值.
 中,
中, ,M是
,M是 边上异于端点的动点,
边上异于端点的动点,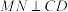 于点N,将矩形
于点N,将矩形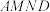 沿
沿 折叠至
折叠至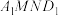 处,使面
处,使面 面
面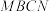 (如图2).点E,F满足
(如图2).点E,F满足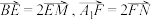 .
.
(1)证明:
 面
面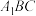 ;
;(2)设
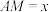 ,当x为何值时,四面体
,当x为何值时,四面体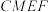 的体积最大,并求出最大值.
的体积最大,并求出最大值.
您最近一年使用:0次
2019-02-05更新
|
710次组卷
|
2卷引用:【全国百强校】湖北省荆州中学、宜昌一中等“荆、荆、襄、宜四地七校考试联盟”2019届高三上学期期末考试数学(文)试题
名校
8 . 如图,在三棱台ABC﹣A1B1C1中,D,E分别是AB,AC的中点,B1E⊥平面ABC,△AB1C是等边三角形,AB=2A1B1,AC=2BC,∠ACB=90°.

(1)证明:B1C∥平面A1DE;
(2)求二面角A﹣BB1﹣C的正弦值.

(1)证明:B1C∥平面A1DE;
(2)求二面角A﹣BB1﹣C的正弦值.
您最近一年使用:0次
2018-12-03更新
|
1282次组卷
|
6卷引用:湖北省恩施州2017-2018学年高三第一次教学质量监测考试理科数学
名校
9 . 如图,在几何体 中,平面
中,平面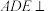 平面
平面 ,四边形
,四边形 为菱形,且
为菱形,且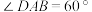 ,
,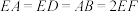 ,
,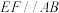 ,
, 为
为 中点.
中点.
(1)求证: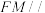 平面
平面 ;
;
(2)求二面角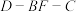 的平面角的正弦值.
的平面角的正弦值.
 中,平面
中,平面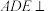 平面
平面 ,四边形
,四边形 为菱形,且
为菱形,且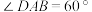 ,
,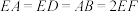 ,
,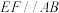 ,
, 为
为 中点.
中点.
(1)求证:
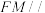 平面
平面 ;
;(2)求二面角
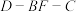 的平面角的正弦值.
的平面角的正弦值.
您最近一年使用:0次
2018-02-15更新
|
968次组卷
|
3卷引用:湖北省荆州中学、宜昌一中等“荆、荆、襄、宜四地七校考试联盟”2018届高三2月联考数学(理)试题2
真题
名校
10 . 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
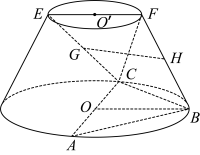
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB= AC=
AC=  ,AB=BC.求二面角
,AB=BC.求二面角 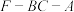 的余弦值.
的余弦值.
 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=
 AC=
AC=  ,AB=BC.求二面角
,AB=BC.求二面角 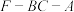 的余弦值.
的余弦值.
您最近一年使用:0次
2016-12-04更新
|
1990次组卷
|
10卷引用:湖北省黄冈中学2021届高三下学期5月适应性考试数学试题
湖北省黄冈中学2021届高三下学期5月适应性考试数学试题2016年全国普通高等学校招生统一考试理科数学(山东卷精编版)(已下线)专题17 立体几何综合-五年(2016-2020)高考数学(理)真题分项河北正定中学2021届高三上学期第四次半月考数学试题沪教版(2020) 一轮复习 堂堂清 第八单元 8.10 空间向量在立体几何中的应用(二)(已下线)2016年全国普通高等学校招生统一考试理科数学(山东卷参考版)(已下线)专题24 空间向量与空间角的计算-十年(2011-2020)高考真题数学分项(已下线)专题23 立体几何解答题(理科)-12016-2017学年河北定州市高二上学期期中数学试卷人教A版高中数学必修二 2.3.2 平面与平面垂直的判定



