名校
解题方法
1 . 如图,在棱长为 的正四面体
的正四面体 中,点
中,点 ,
, 分别为
分别为 和
和 的重心,
的重心, 为线段
为线段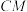 上一点.则下列结论正确的是( )
上一点.则下列结论正确的是( )
 的正四面体
的正四面体 中,点
中,点 ,
, 分别为
分别为 和
和 的重心,
的重心, 为线段
为线段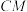 上一点.则下列结论正确的是( )
上一点.则下列结论正确的是( )
A.若 平面 平面 ,则 ,则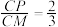 |
B.若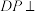 平面 平面 ,则三棱锥 ,则三棱锥 的体积为 的体积为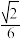 |
C.若 为线段 为线段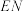 的中点,且 的中点,且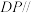 平面 平面 ,则 ,则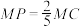 |
D. 的最小值为2 的最小值为2 |
您最近一年使用:0次
名校
解题方法
2 . 在棱长为2的正方体 中,动点
中,动点 在正方形
在正方形 内运动(含边界),则( )
内运动(含边界),则( )
 中,动点
中,动点 在正方形
在正方形 内运动(含边界),则( )
内运动(含边界),则( )A.有且仅有一个点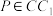 ,使得 ,使得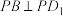 |
B.有且仅有一个点 ,使得 ,使得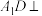 平面 平面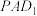 |
C.当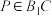 时,三棱锥 时,三棱锥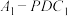 的体积为定值 的体积为定值 |
D.有且仅有两个点 ,使得 ,使得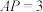 |
您最近一年使用:0次
2024·全国·模拟预测
解题方法
3 . 在三棱锥 中,底面
中,底面 是等边三角形,侧面
是等边三角形,侧面 是等腰直角三角形,
是等腰直角三角形,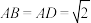 ,
, 是平面
是平面 内一点,且
内一点,且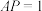 ,若
,若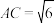 ,则点
,则点 的轨迹长度为( )
的轨迹长度为( )
 中,底面
中,底面 是等边三角形,侧面
是等边三角形,侧面 是等腰直角三角形,
是等腰直角三角形,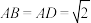 ,
, 是平面
是平面 内一点,且
内一点,且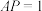 ,若
,若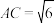 ,则点
,则点 的轨迹长度为( )
的轨迹长度为( )A. | B. | C.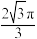 | D. |
您最近一年使用:0次
名校
解题方法
4 . 已知正六棱锥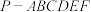 的侧棱长为
的侧棱长为 ,底面边长为2,点
,底面边长为2,点 为正六棱锥
为正六棱锥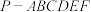 外接球上一点,则三棱锥
外接球上一点,则三棱锥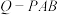 体积的最大值为( )
体积的最大值为( )
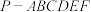 的侧棱长为
的侧棱长为 ,底面边长为2,点
,底面边长为2,点 为正六棱锥
为正六棱锥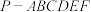 外接球上一点,则三棱锥
外接球上一点,则三棱锥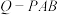 体积的最大值为( )
体积的最大值为( )
A. | B.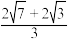 | C. | D.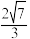 |
您最近一年使用:0次
2023-09-01更新
|
714次组卷
|
5卷引用:福建省龙岩市一级校联盟2022-2023学年高一下学期期中联考数学试题
福建省龙岩市一级校联盟2022-2023学年高一下学期期中联考数学试题(已下线)模块一专题6《简单几何体的表面积和体积》单元检测篇B提升卷(已下线)第13讲 8.6.2直线与平面垂直的性质定理 (第2课时)-【帮课堂】(人教A版2019必修第二册)江西省吉安市第三中学2023-2024学年高二上学期开学考试(艺术类)数学试题(已下线)第11章 简单几何体(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020必修第三册)
解题方法
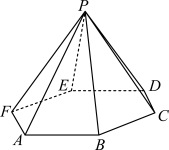
5 . 如图所示,已知四棱锥 中,
中,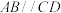 ,
, ,
, ,
,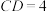 ,
, ,
,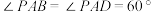

(1)图(1)若点 为
为 的中点,求证:
的中点,求证: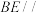 平面
平面
(2)图(1)求证:顶点 在底面
在底面 的射影为边
的射影为边 的中点.
的中点.
(3)图(2)点 在
在 上,且
上,且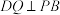 ,求三棱锥
,求三棱锥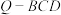 的体积.
的体积.
 中,
中,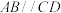 ,
, ,
, ,
,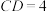 ,
, ,
,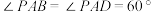

(1)图(1)若点
 为
为 的中点,求证:
的中点,求证: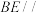 平面
平面
(2)图(1)求证:顶点
 在底面
在底面 的射影为边
的射影为边 的中点.
的中点.(3)图(2)点
 在
在 上,且
上,且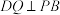 ,求三棱锥
,求三棱锥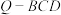 的体积.
的体积.
您最近一年使用:0次
名校
6 . 在棱长为 的正方体
的正方体 中,
中, 为正方形
为正方形 的中心,
的中心, 为棱
为棱 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )

 的正方体
的正方体 中,
中, 为正方形
为正方形 的中心,
的中心, 为棱
为棱 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
A.点 为 为 中点时, 中点时,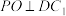 |
B.点 与点 与点 重合时,三棱锥 重合时,三棱锥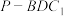 外接球体积为 外接球体积为 |
C.当 点运动时,三棱锥 点运动时,三棱锥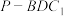 外接球的球心总在直线 外接球的球心总在直线 上 上 |
D.当 为 为 的中点时,正方体表面到 的中点时,正方体表面到 点距离为 点距离为 的轨迹的总长度为 的轨迹的总长度为 |
您最近一年使用:0次
2022-01-08更新
|
2671次组卷
|
10卷引用:福建省泉州第五中学2021-2022学年高一下学期期中考试数学试题
福建省泉州第五中学2021-2022学年高一下学期期中考试数学试题福建省南平市浦城县2022-2023学年高一下学期期中考试数学试题湖南省名校联考联合体2021-2022学年高二上学期12月联考数学试题(已下线)数学-2022届高三下学期开学摸底考试卷(山东专用)辽宁省鞍山市第一中学2021-2022学年高三下学期4月线上模拟考试数学试卷山东省五莲县、诸城市、安丘市、兰山区四县区2022届高三过程性测试数学试题湖南省株洲市第二中学2021-2022学年高二下学期第二次月考数学试题湖南省株洲市南方中学2022-2023学年高三上学期9月月考数学试题(已下线)考点14 立体几何中的动态问题 2024届高考数学考点总动员【讲】重庆外国语学校(川外附中)2024届高三上学期1月月考数学试题
名校
解题方法
7 . 如图,在边长为2的正方形 中,点
中,点 是边
是边 的中点,将
的中点,将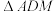 沿
沿 翻折到
翻折到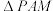 ,连结
,连结 ,
,  ,在
,在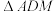 翻折到
翻折到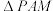 的过程中,下列说法正确的是
的过程中,下列说法正确的是_________ .(将正确说法的序号都写上)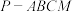 的体积的最大值为
的体积的最大值为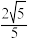 ;
;
②当面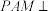 平面
平面 时,二面角
时,二面角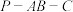 的正切值为
的正切值为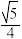 ;
;
③存在某一翻折位置,使得 ;
;
④棱 的中点为
的中点为 ,则
,则 的长为定值.
的长为定值.
 中,点
中,点 是边
是边 的中点,将
的中点,将 沿
沿 翻折到
翻折到 ,连结
,连结 ,
,  ,在
,在 翻折到
翻折到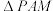 的过程中,下列说法正确的是
的过程中,下列说法正确的是
 的体积的最大值为
的体积的最大值为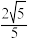 ;
;②当面
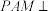 平面
平面 时,二面角
时,二面角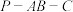 的正切值为
的正切值为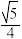 ;
;③存在某一翻折位置,使得
 ;
;④棱
 的中点为
的中点为 ,则
,则 的长为定值.
的长为定值.
您最近一年使用:0次
2021-12-10更新
|
1107次组卷
|
3卷引用:福建省浦城第一中学2023-2024学年高一下学期4月期中考试数学试题
福建省浦城第一中学2023-2024学年高一下学期4月期中考试数学试题黑龙江省哈尔滨师范大学附属中学2021-2022学年高三上学期期中考试数学(理)试题(已下线)第八章 立体几何初步(提分小卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(人教A版2019必修第二册)



