名校
解题方法
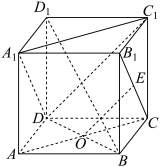
1 . 在棱长为1的正方体 中,
中,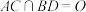 ,E是线段
,E是线段 (含端点)上的一动点,
(含端点)上的一动点,
① ;
;
②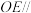 平面
平面 ;
;
③三棱锥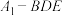 的体积为定值;
的体积为定值;
④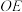 与
与 所成的最大角为
所成的最大角为 .
.
上述命题中正确的个数是( )
 中,
中,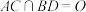 ,E是线段
,E是线段 (含端点)上的一动点,
(含端点)上的一动点,①
 ;
;②
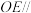 平面
平面 ;
;③三棱锥
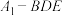 的体积为定值;
的体积为定值;④
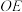 与
与 所成的最大角为
所成的最大角为 .
.上述命题中正确的个数是( )
| A.4 | B.3 | C.2 | D.1 |
您最近一年使用:0次
2024-07-15更新
|
728次组卷
|
4卷引用:第2套 考前押题卷(高一期末)
名校
2 . 已知正四面体 的棱长为
的棱长为 ,
, 为
为 的重心,
的重心, 为线段
为线段 上一点,则( )
上一点,则( )
 的棱长为
的棱长为 ,
, 为
为 的重心,
的重心, 为线段
为线段 上一点,则( )
上一点,则( )A. |
B.正四面体的体积为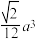 |
C.正四面体的外接球的体积为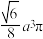 |
D. 点到各个面的距离之和为定值,且定值为 点到各个面的距离之和为定值,且定值为 |
您最近一年使用:0次
2024-07-02更新
|
803次组卷
|
3卷引用:第1套 全真模拟卷 (较难)【高一期末复习全真模拟】
(已下线)第1套 全真模拟卷 (较难)【高一期末复习全真模拟】广东省江门市某校2023-2024学年高一下学期期末热身模拟数学试题四川省泸州市泸县第五中学2023-2024学年高一下学期6月期末考试数学试题
名校
3 . 如图,在四棱锥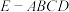 中,
中, 平面
平面 ,
,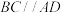 ,且
,且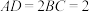 ,
, 是
是 的中点.
的中点. ;
;
(2)若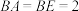 ,直线
,直线 与直线
与直线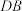 所成角的余弦值为
所成角的余弦值为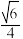 .
.
(ⅰ)求直线 与平面
与平面 所成角;
所成角;
(ⅱ)求二面角 的余弦值.
的余弦值.
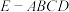 中,
中, 平面
平面 ,
,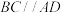 ,且
,且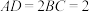 ,
, 是
是 的中点.
的中点.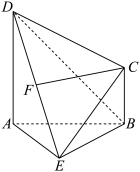
 ;
;(2)若
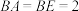 ,直线
,直线 与直线
与直线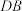 所成角的余弦值为
所成角的余弦值为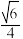 .
.(ⅰ)求直线
 与平面
与平面 所成角;
所成角;(ⅱ)求二面角
 的余弦值.
的余弦值.
您最近一年使用:0次
2024-06-18更新
|
1318次组卷
|
7卷引用:第24题 垂直的证明(高一期末每日一题)
(已下线)第24题 垂直的证明(高一期末每日一题)江苏省如皋市2023-2024学年高一下学期教学质量调研(二)数学试题四川省泸州市江阳区2023-2024学年高一下学期6月期末数学试题宁夏回族自治区银川一中2023-2024学年高一下学期期末考试数学试卷安徽省六安第二中学河西校区2023-2024学年高一下学期6月期末考试数学试题(已下线)专题11 立体几何测试卷- 【暑假自学课】(沪教版2020)广西百色市平果市铝城中学2024-2025学年高二上学期开学收心考试数学试卷
4 . 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马 中,侧棱
中,侧棱 底面ABCD,且
底面ABCD,且 ,点E是PC的中点,连接DE、BD、BE.
,点E是PC的中点,连接DE、BD、BE. 平面
平面 .试判断四面体
.试判断四面体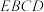 是否为鳖臑.若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑.若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(2)设H点是AD的中点,若面EDB与面ABCD所成二面角的大小为 ,求四棱锥
,求四棱锥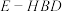 的外接球的表面积.
的外接球的表面积.
 中,侧棱
中,侧棱 底面ABCD,且
底面ABCD,且 ,点E是PC的中点,连接DE、BD、BE.
,点E是PC的中点,连接DE、BD、BE.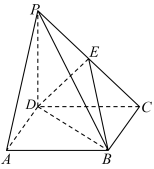
 平面
平面 .试判断四面体
.试判断四面体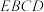 是否为鳖臑.若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑.若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;(2)设H点是AD的中点,若面EDB与面ABCD所成二面角的大小为
 ,求四棱锥
,求四棱锥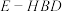 的外接球的表面积.
的外接球的表面积.
您最近一年使用:0次
2024-06-11更新
|
534次组卷
|
4卷引用:专题2 以立体几何为背景的各类证明和计算问题【练】(高一期末压轴专项)
(已下线)专题2 以立体几何为背景的各类证明和计算问题【练】(高一期末压轴专项)浙江省浙江山海共富联盟2023-2024学年高一下学期6月联考数学试题福建省部分学校2023-2024学年高一下学期联合测评数学试卷(已下线)专题4 立体几何中的新定义压轴大题(二)【讲】
名校
解题方法
5 . 故宫角楼的屋顶是我国十字脊顶的典型代表,如图1,它是由两个完全相同的直三棱柱垂直交叉构成,将其抽象成几何体如图2所示.已知三楼柱 和
和 是两个完全相同的直三棱柱,侧棱
是两个完全相同的直三棱柱,侧棱 与
与 互相垂直平分,
互相垂直平分,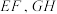 交于点I,
交于点I,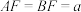 ,
, ,则点
,则点 到平面
到平面 的距离是( )
的距离是( )
 和
和 是两个完全相同的直三棱柱,侧棱
是两个完全相同的直三棱柱,侧棱 与
与 互相垂直平分,
互相垂直平分,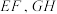 交于点I,
交于点I,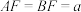 ,
, ,则点
,则点 到平面
到平面 的距离是( )
的距离是( )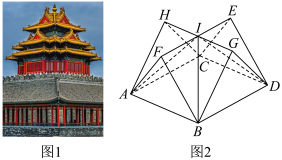
A. | B.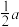 | C.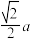 | D.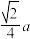 |
您最近一年使用:0次
2024-05-28更新
|
1140次组卷
|
7卷引用:第3套 全真模拟卷 (较难)【高一期末复习全真模拟】
(已下线)第3套 全真模拟卷 (较难)【高一期末复习全真模拟】福建省部分优质高中2023-2024学年高一下学期期末质量检测数学试卷山东省部分学校2023-2024学年高一下学期联合测评数学试卷(已下线)周测15 空间平行与垂直的关系(北京专版 )北京市中国人民大学附属中学2024届高三下学期5月热身练习数学试题(三模)(已下线)【北京专用】高二下学期期末模拟测试A卷2024届河北省承德市部分示范高中高三三模数学试题
名校
解题方法
6 . 如图,在四棱锥P-ABCD中,底面ABCD为菱形, ,
,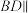 平面AMHN,点M,N,H分别在棱PB,PD,PC上,且
平面AMHN,点M,N,H分别在棱PB,PD,PC上,且 .
.
(1)证明: ;
;
(2)若H为PC的中点,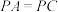 ,PA与平面PBD所成角为60°,四棱锥
,PA与平面PBD所成角为60°,四棱锥 被平面
被平面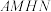 截为两部分,记四棱锥
截为两部分,记四棱锥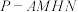 体积为
体积为 ,另一部分体积为
,另一部分体积为 ,求
,求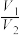 .
.
 ,
,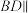 平面AMHN,点M,N,H分别在棱PB,PD,PC上,且
平面AMHN,点M,N,H分别在棱PB,PD,PC上,且 .
.
(1)证明:
 ;
;(2)若H为PC的中点,
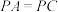 ,PA与平面PBD所成角为60°,四棱锥
,PA与平面PBD所成角为60°,四棱锥 被平面
被平面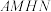 截为两部分,记四棱锥
截为两部分,记四棱锥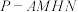 体积为
体积为 ,另一部分体积为
,另一部分体积为 ,求
,求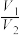 .
.
您最近一年使用:0次
2024-05-13更新
|
1614次组卷
|
4卷引用:第19题 线面角的求解(高一期末每日一题)
(已下线)第19题 线面角的求解(高一期末每日一题)(已下线)期末押题卷02(考试范围:苏教版2019必修第二册)-【帮课堂】(苏教版2019必修第二册)安徽省淮南第二中学2023-2024学年高一下学期5月月考数学试题山东省临沂市2024届高三下学期5月高考模拟考试(二模)数学试题
2024·全国·模拟预测
解题方法
7 . 如图,在直三棱柱 中,
中,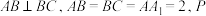 为线段
为线段 的中点,
的中点, 为线段
为线段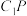 (包括端点)上一点,则
(包括端点)上一点,则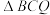 的面积的取值范围为
的面积的取值范围为______ .
 中,
中,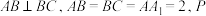 为线段
为线段 的中点,
的中点, 为线段
为线段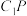 (包括端点)上一点,则
(包括端点)上一点,则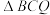 的面积的取值范围为
的面积的取值范围为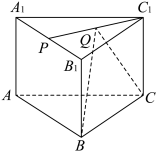
您最近一年使用:0次
解题方法
8 . 在棱长为1的正方体 中,过面对角线
中,过面对角线 的平面记为
的平面记为 ,以下四个命题:
,以下四个命题: ,使
,使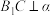 ;
;
②若平面 与平面
与平面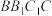 的交线为
的交线为 ,则存在直线
,则存在直线 ,使
,使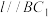 ;
;
③若平面 截正方体所得的截面为三角形,则该截面三角形面积的最大值为
截正方体所得的截面为三角形,则该截面三角形面积的最大值为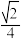 ;
;
④若平面 过点
过点 ,点
,点 在线段
在线段 上运动,则点
上运动,则点 到平面
到平面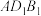 的距离为
的距离为 .
.
其中真命题的序号为____________ .
 中,过面对角线
中,过面对角线 的平面记为
的平面记为 ,以下四个命题:
,以下四个命题:
 ,使
,使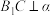 ;
;②若平面
 与平面
与平面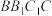 的交线为
的交线为 ,则存在直线
,则存在直线 ,使
,使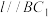 ;
;③若平面
 截正方体所得的截面为三角形,则该截面三角形面积的最大值为
截正方体所得的截面为三角形,则该截面三角形面积的最大值为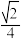 ;
;④若平面
 过点
过点 ,点
,点 在线段
在线段 上运动,则点
上运动,则点 到平面
到平面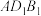 的距离为
的距离为 .
.其中真命题的序号为
您最近一年使用:0次
2024·四川成都·模拟预测
名校
9 . 在四棱锥 中,
中, 平面
平面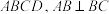 ,且
,且 .若点
.若点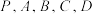 均在球
均在球 的表面上,则球
的表面上,则球 的体积的最小值为( )
的体积的最小值为( )
 中,
中, 平面
平面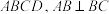 ,且
,且 .若点
.若点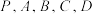 均在球
均在球 的表面上,则球
的表面上,则球 的体积的最小值为( )
的体积的最小值为( )A.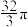 | B. | C.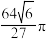 | D. |
您最近一年使用:0次
2024-03-06更新
|
604次组卷
|
8卷引用:高一下学期期中复习选择题压轴题十七大题型专练(2)-举一反三系列(人教A版2019必修第二册)
(已下线)高一下学期期中复习选择题压轴题十七大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)第3讲:立体几何中的探究问题【练】(已下线)专题2 球组合体 补体性质 练(已下线)四川省成都市第七中学2024届高三下学期二诊模拟考试文科数学试卷(已下线)四川省成都市第七中学2024届高三下学期二诊模拟考试理科数学试卷广东省广州市第六中学2023-2024学年高二下学期3月测验数学试题湖南省长沙市浏阳市重点校联考2024届高三下学期期中测试数学试卷河南省许昌市部分学校2024届高三下学期高考冲刺(一)数学试题
名校
解题方法
10 . 如图所示,三棱锥 中,
中,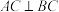 ,
,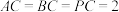 ,
, 为线段
为线段 上的动点(
上的动点( 不与
不与 重合),且
重合),且 ,则( )
,则( )
 中,
中,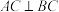 ,
,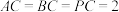 ,
, 为线段
为线段 上的动点(
上的动点( 不与
不与 重合),且
重合),且 ,则( )
,则( )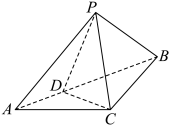
A.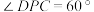 |
B. |
C.存在点 ,使得 ,使得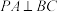 |
D.三棱锥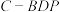 的体积有最大值 的体积有最大值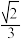 |
您最近一年使用:0次



