1 . 如图,在直棱柱 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, .点
.点 是线段
是线段 上的动点(不含端点),
上的动点(不含端点), 为
为 的中点.
的中点.

(1)当 为
为 的中点时,证明:
的中点时,证明: 平面
平面 ;
;
(2)当 时,求点
时,求点 到平面
到平面 的距离.
的距离.
 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, .点
.点 是线段
是线段 上的动点(不含端点),
上的动点(不含端点), 为
为 的中点.
的中点.
(1)当
 为
为 的中点时,证明:
的中点时,证明: 平面
平面 ;
;(2)当
 时,求点
时,求点 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2021-06-20更新
|
2782次组卷
|
4卷引用:河南省商丘市第一高级中学2020-2021学年高三5月月考文科数学试题
河南省商丘市第一高级中学2020-2021学年高三5月月考文科数学试题(已下线)考点33 直线、平面平行的判定及其性质-备战2022年高考数学(理)一轮复习考点帮(已下线)考点32 直线、平面平行的判定及其性质-备战2022年高考数学(文)一轮复习考点帮河南省洛阳市第十九中学2021-2022学年高一下学期6月月考数学试题
2 . 如图,正方体ABCD -A1B1C1D1中,E为棱C1D1的中点,F为棱BC的中点.

(1)求证:直线AE⊥直线A1D;
(2)在线段AA1上求一点G,使得直线AE⊥平面DFG.

(1)求证:直线AE⊥直线A1D;
(2)在线段AA1上求一点G,使得直线AE⊥平面DFG.
您最近一年使用:0次
3 . 四棱锥 中,底面
中,底面 为矩形
为矩形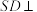 底面
底面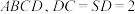 ,点M是侧棱
,点M是侧棱 的中点,
的中点,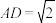 .
.
(1)求异面直线 与
与 所成角的大小;
所成角的大小;
(2)求二面角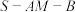 的正弦值.
的正弦值.
 中,底面
中,底面 为矩形
为矩形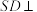 底面
底面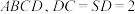 ,点M是侧棱
,点M是侧棱 的中点,
的中点,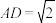 .
.
(1)求异面直线
 与
与 所成角的大小;
所成角的大小;(2)求二面角
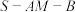 的正弦值.
的正弦值.
您最近一年使用:0次
名校
解题方法
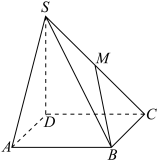
4 . 如图所示,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 为侧棱
为侧棱 的中点.
的中点.
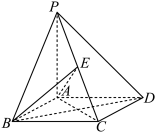
(1)设经过 、
、 、
、 三点的平面交
三点的平面交 于
于 ,证明:
,证明: 为
为 的中点;
的中点;
(2)若 底面
底面 ,且
,且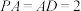 ,求四面体
,求四面体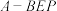 的体积.
的体积.
 中,底面
中,底面 为正方形,
为正方形, 为侧棱
为侧棱 的中点.
的中点.
(1)设经过
 、
、 、
、 三点的平面交
三点的平面交 于
于 ,证明:
,证明: 为
为 的中点;
的中点;(2)若
 底面
底面 ,且
,且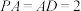 ,求四面体
,求四面体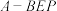 的体积.
的体积.
您最近一年使用:0次
2021-08-09更新
|
1247次组卷
|
4卷引用:江苏省南通市如皋中学2020-2021学年高一下学期第二次阶段考试数学试题
名校
解题方法
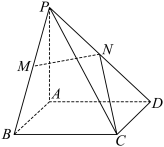
5 . 如图,四棱锥 中,
中, 平面
平面 ,四边形
,四边形 为正方形,点M、N分别为直线
为正方形,点M、N分别为直线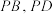 上的点,且满足
上的点,且满足 .
.
(1)求证: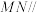 平面
平面 ;
;
(2)若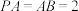 ,
,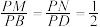 ,求点
,求点 到平面
到平面 的距离.
的距离.
 中,
中, 平面
平面 ,四边形
,四边形 为正方形,点M、N分别为直线
为正方形,点M、N分别为直线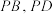 上的点,且满足
上的点,且满足 .
.
(1)求证:
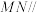 平面
平面 ;
;(2)若
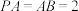 ,
,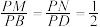 ,求点
,求点 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2021-06-02更新
|
1290次组卷
|
4卷引用:江西省南昌市第二中学、河南省实验中学2021届高三5月冲刺联考数学(文)试题1
江西省南昌市第二中学、河南省实验中学2021届高三5月冲刺联考数学(文)试题1(已下线)期末测试卷02-2020-2021学年高一数学下学期期末专项复习(北师大版2019必修第二册)江西省南昌市第二中学、河南省实验中学2021届高三5月冲刺联考数学(文)试题2湖南省邵阳市第二中学2022-2023学年高一下学期期中数学试题
6 . 如图,一块正方体形木料的上底面有一点E.若经过点E在上底面上画一条直线与CE垂直,则应该怎样画?

您最近一年使用:0次
2020-02-02更新
|
1244次组卷
|
4卷引用:人教A版(2019) 必修第二册 逆袭之路 第八章 立体几何初步 小结 复习参考题 8
人教A版(2019) 必修第二册 逆袭之路 第八章 立体几何初步 小结 复习参考题 8(已下线)13.2.3 直线与平面的位置关系苏教版(2019)必修第二册课本习题 习题13.2(3)(已下线)复习参考题8
7 . 下列各种说法正确吗?为什么?
(1)如果一条直线和一个平面内的无数条直线都垂直,那么这条直线和这个平面垂直;
(2)如果一条直线和一个平面内的任意两条直线都垂直,那么这条直线和这个平面垂直;
(3)如果一条直线和一个平面内的两条相交直线垂直,那么这条直线和这个平面垂直.
(1)如果一条直线和一个平面内的无数条直线都垂直,那么这条直线和这个平面垂直;
(2)如果一条直线和一个平面内的任意两条直线都垂直,那么这条直线和这个平面垂直;
(3)如果一条直线和一个平面内的两条相交直线垂直,那么这条直线和这个平面垂直.
您最近一年使用:0次
2023-10-09更新
|
184次组卷
|
4卷引用:北师大版(2019)必修第二册课本习题第六章5.1直线与平面垂直
北师大版(2019)必修第二册课本习题第六章5.1直线与平面垂直(已下线)第八章 立体几何初步 单元复习提升(易错与拓展)(1)-单元速记·巧练(人教A版2019必修第二册)(已下线)5.1 直线与平面垂直北师大版(2019)必修第二册课本例题5.1 直线与平面垂直
8 . 如图:四面体 的底面
的底面 是直角三角形,
是直角三角形,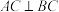 ,
, ,
,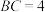 ,
,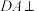 平面
平面 ,
,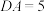 ,
, 是
是 上的动点(不包括端点).
上的动点(不包括端点).
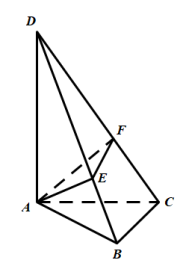
(1)求证: 与
与 不垂直;
不垂直;
(2)当 时,求
时,求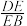 的值.
的值.
 的底面
的底面 是直角三角形,
是直角三角形,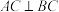 ,
, ,
,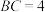 ,
,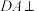 平面
平面 ,
,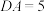 ,
, 是
是 上的动点(不包括端点).
上的动点(不包括端点). 
(1)求证:
 与
与 不垂直;
不垂直;(2)当
 时,求
时,求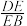 的值.
的值.
您最近一年使用:0次
2019-11-11更新
|
450次组卷
|
3卷引用:2019年上海市建平中学高三三模数学试题
名校
9 . 在棱长为 的正方体
的正方体 中,
中, 、
、 分别是棱
分别是棱 、
、 上的点,且
上的点,且 .
.
(1)当 、
、 在何位置时,
在何位置时,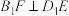 ?
?
(2)是否存在点 、
、 ,使
,使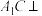 面
面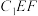 ?
?
(3)当 、
、 在何位置时三棱锥
在何位置时三棱锥 的体积取得最大值?并求此时二面角
的体积取得最大值?并求此时二面角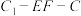 的大小.
的大小.
 的正方体
的正方体 中,
中, 、
、 分别是棱
分别是棱 、
、 上的点,且
上的点,且 .
.(1)当
 、
、 在何位置时,
在何位置时,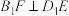 ?
?(2)是否存在点
 、
、 ,使
,使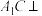 面
面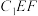 ?
?(3)当
 、
、 在何位置时三棱锥
在何位置时三棱锥 的体积取得最大值?并求此时二面角
的体积取得最大值?并求此时二面角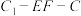 的大小.
的大小.
您最近一年使用:0次
2019-11-11更新
|
347次组卷
|
2卷引用:上海市行知中学2018-2019学年高二下学期期中数学试题
10 . 如图所示,三棱柱 的侧面
的侧面 是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点.
是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点.

(1)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线 与AB的所成角的大小(结果用反三角函数值表示);
与AB的所成角的大小(结果用反三角函数值表示);
(2)当点C是弧AB的中点时,求四棱锥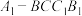 体积与圆柱体积的比.
体积与圆柱体积的比.
 的侧面
的侧面 是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点.
是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点.
(1)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线
 与AB的所成角的大小(结果用反三角函数值表示);
与AB的所成角的大小(结果用反三角函数值表示);(2)当点C是弧AB的中点时,求四棱锥
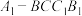 体积与圆柱体积的比.
体积与圆柱体积的比.
您最近一年使用:0次
2019-11-06更新
|
326次组卷
|
6卷引用:【全国百强校】上海市交大附中2019届高三9月开学摸底考试数学试题



