1 . 如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,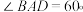 ,
, ,
, 为
为 的中点.
的中点. 平面
平面 ;
;
(2)若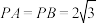 ,
,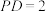 .
.
①求二面角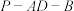 的余弦值;
的余弦值;
②求直线 与平面
与平面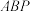 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 为菱形,
为菱形,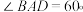 ,
, ,
, 为
为 的中点.
的中点.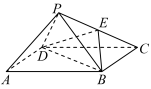
 平面
平面 ;
;(2)若
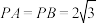 ,
,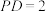 .
.①求二面角
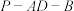 的余弦值;
的余弦值;②求直线
 与平面
与平面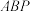 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
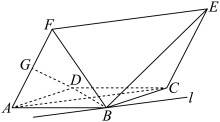
2 . 如图,已知四边形 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,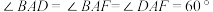 .
. 平面
平面 ;
;
(2)设平面 平面
平面 ,且二面角
,且二面角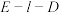 的平面角为
的平面角为 ,
,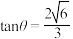 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,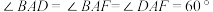 .
.
 平面
平面 ;
;(2)设平面
 平面
平面 ,且二面角
,且二面角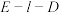 的平面角为
的平面角为 ,
,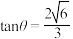 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-22更新
|
778次组卷
|
3卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
名校
3 . 如图,已知正三棱台 由一个平面截棱长为6的正四面体所得,
由一个平面截棱长为6的正四面体所得,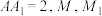 分别是
分别是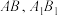 的中点,P是棱台的侧面
的中点,P是棱台的侧面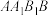 上的动点(包含边界),则下列结论中正确的是( )
上的动点(包含边界),则下列结论中正确的是( )
 由一个平面截棱长为6的正四面体所得,
由一个平面截棱长为6的正四面体所得,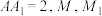 分别是
分别是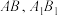 的中点,P是棱台的侧面
的中点,P是棱台的侧面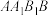 上的动点(包含边界),则下列结论中正确的是( )
上的动点(包含边界),则下列结论中正确的是( )
A.该三棱台的体积为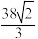 |
B.平面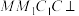 平面 平面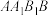 |
C.直线 与平面 与平面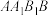 所成角的正切值的最小值为 所成角的正切值的最小值为 |
D.若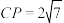 ,则点 ,则点 的轨迹的长度为 的轨迹的长度为 |
您最近一年使用:0次
2024-07-20更新
|
337次组卷
|
2卷引用:辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷
4 . 如图,在四棱柱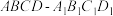 中,平面
中,平面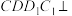 平面
平面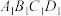 ,
,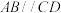 ,
, ,
,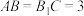 ,
,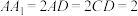 .
. 平面
平面 ;
;
(2)求直线 与平面
与平面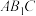 所成角的正弦值.
所成角的正弦值.
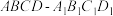 中,平面
中,平面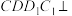 平面
平面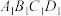 ,
,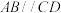 ,
, ,
,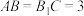 ,
,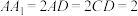 .
.
 平面
平面 ;
;(2)求直线
 与平面
与平面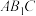 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-09更新
|
554次组卷
|
2卷引用:辽宁省辽阳市2023-2024学年高一下学期期末考试数学试卷
名校
5 . 如图在四棱锥 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且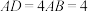 ,
, ,
,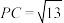 ,点E为AD中点,
,点E为AD中点, 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)点F为对角线AC上的点,且 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且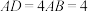 ,
, ,
,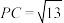 ,点E为AD中点,
,点E为AD中点,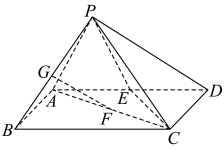
 平面
平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3)点F为对角线AC上的点,且
 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
您最近一年使用:0次
2024-06-23更新
|
860次组卷
|
4卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷浙东北联盟(ZDB)四校2023-2024学年高一下学期期中考试数学试卷(已下线)第3套 全真模拟卷 (中等)【高一期末复习全真模拟】河南省信阳市息县第二高级中学联考2023-2024学年高一下学期7月期末考试数学试题
2024高三·全国·专题练习
名校
6 . 如图,四面体 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.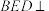 平面
平面 ;
;
(2)设 ,
,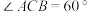 ,点
,点 在
在 上;
上;
①点 为
为 中点,求
中点,求 与
与 所成角的余弦值;
所成角的余弦值;
②当 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
 中,
中, ,
, ,
, ,
, 为
为 的中点.
的中点.
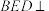 平面
平面 ;
;(2)设
 ,
,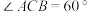 ,点
,点 在
在 上;
上;①点
 为
为 中点,求
中点,求 与
与 所成角的余弦值;
所成角的余弦值;②当
 的面积最小时,求
的面积最小时,求 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
您最近一年使用:0次
2024-03-18更新
|
1737次组卷
|
5卷引用:辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷
辽宁省五校联考2023-2024学年高一下学期期末考试数学试卷山西省临汾市侯马市第一中学校2023-2024学年高一下学期第三次月考数学试题江西省宜春市丰城市第九中学2023-2024学年高一下学期7月期末考试数学试题辽宁省鞍山市第一中学等校2023-2024学年高一下学期7月期末考试数学试题(已下线)第二章 立体几何中的计算 专题一 空间角 微点5 直线与平面所成角综合训练【培优版】
名校
解题方法
7 . 在正方体 中,棱
中,棱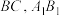 的中点分别为
的中点分别为 ,
, ,则直线
,则直线 与平面
与平面 所成角的正弦值为( )
所成角的正弦值为( )
 中,棱
中,棱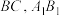 的中点分别为
的中点分别为 ,
, ,则直线
,则直线 与平面
与平面 所成角的正弦值为( )
所成角的正弦值为( )A.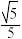 | B.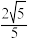 | C.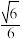 | D.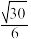 |
您最近一年使用:0次
2024-02-25更新
|
929次组卷
|
8卷引用:辽宁省沈阳市东北育才学校2023-2024学年高一下学期5月月考数学试卷
辽宁省沈阳市东北育才学校2023-2024学年高一下学期5月月考数学试卷(已下线)第13章 立体几何初步(提升卷)-重难点突破及混淆易错规避(苏教版2019必修第二册)天津市汇文中学2023-2024学年高一下学期期中考试数学试题黑龙江省大庆市大庆中学2023-2024学年高一下学期5月期中考试数学试题(已下线)核心考点7 立体几何中角和距离 A基础卷 (高一期末考试必考的10大核心考点)1号卷·A10联盟2022届全国高考第一轮总复习试卷数学(理科)试题(十五)(已下线)重难点6-1 空间角与空间距离的求解(8题型+满分技巧+限时检测)广东省惠州市2024-2025学年高三第二次调研考试(期中)数学试题
名校
8 . 在棱长为1的正方体 中,
中, 为侧面
为侧面 内的一个动点(含边界),则下列说法正确的是( )
内的一个动点(含边界),则下列说法正确的是( )
 中,
中, 为侧面
为侧面 内的一个动点(含边界),则下列说法正确的是( )
内的一个动点(含边界),则下列说法正确的是( )A.随着 点移动,三棱锥 点移动,三棱锥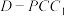 的体积有最小值为 的体积有最小值为 |
B.三棱锥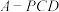 体积的最大值为 体积的最大值为 |
C.直线 与平面 与平面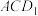 所成角的余弦值为 所成角的余弦值为 |
D.作体对角线 的垂面 的垂面 ,则平面 ,则平面 截此正方体所得截面图形的面积越大,其周长越大 截此正方体所得截面图形的面积越大,其周长越大 |
您最近一年使用:0次
2023-08-12更新
|
912次组卷
|
7卷引用:辽宁省鞍山市台安县高级中学2022-2023学年高一下学期期末数学试题
辽宁省鞍山市台安县高级中学2022-2023学年高一下学期期末数学试题辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题(已下线)专题08立体几何期末14种常考题型归类(2) -期末真题分类汇编(人教B版2019必修第四册)(已下线)专题04 立体几何初步-期期末真题分类汇编(人教A版2019必修第二册)河北省沧州市部分学校2023-2024学年高一下学期5月联考数学试题江西省全南中学2023-2024学年高二上学期开学考试数学试题(已下线)湖南省长沙市雅礼中学2024届高三上学期月考(二)数学试题变式题11-14
解题方法
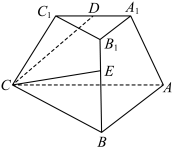
9 . 在正三棱台 中,
中, ,
,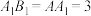 ,
, 为
为 中点,
中点, 在
在 上,
上, .
. 与平面
与平面 的交点
的交点 ,并写出
,并写出 与
与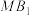 的比值(在图中保留作图痕迹,不必写出画法和理由);
的比值(在图中保留作图痕迹,不必写出画法和理由);
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
,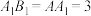 ,
, 为
为 中点,
中点, 在
在 上,
上, .
.
 与平面
与平面 的交点
的交点 ,并写出
,并写出 与
与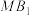 的比值(在图中保留作图痕迹,不必写出画法和理由);
的比值(在图中保留作图痕迹,不必写出画法和理由);(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-08-02更新
|
1724次组卷
|
6卷引用:辽宁省大连市2022-2023学年高一下学期期末数学试题
辽宁省大连市2022-2023学年高一下学期期末数学试题(已下线)第八章 立体几何初步(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)重难点专题13 轻松搞定线面角问题-【帮课堂】(苏教版2019必修第二册)(已下线)专题02 高一下期末真题精选(2)-期末考点大串讲(人教A版2019必修第二册)广东省阳江市2024届高三上学期开学适应性考试数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离(四大题型)
名校
10 . 如图,在直三棱柱 中,
中,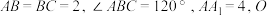 为
为 的中点,
的中点, 为
为 上的动点,
上的动点, 在
在 上,且满足
上,且满足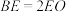 .现延长
.现延长 至
至 点,使得
点,使得 .
.

(1)若二面角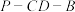 的平面角为
的平面角为 ,求
,求 的长;
的长;
(2)若三棱锥 的体积为
的体积为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,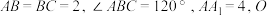 为
为 的中点,
的中点, 为
为 上的动点,
上的动点, 在
在 上,且满足
上,且满足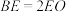 .现延长
.现延长 至
至 点,使得
点,使得 .
.
(1)若二面角
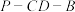 的平面角为
的平面角为 ,求
,求 的长;
的长;(2)若三棱锥
 的体积为
的体积为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-07-27更新
|
1293次组卷
|
6卷引用:辽宁省鞍山市台安县高级中学2022-2023学年高一下学期期末数学试题
辽宁省鞍山市台安县高级中学2022-2023学年高一下学期期末数学试题江西省南昌市等5地2022-2023学年高一下学期期末联考数学试题辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题(已下线)第八章 立体几何初步(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)重组8 高一期末真题重组卷(辽宁卷)A基础卷山西省太原师范学院附属中学(太原市师苑中学校)2023-2024学年高二上学期开学分班测评数学试题



