1 . 如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, ,
, ,
, ,D,E分别为
,D,E分别为 ,
, 的中点.
的中点.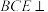 平面
平面 .
.
(2)求平面 与平面
与平面 的夹角的余弦值.
的夹角的余弦值.
 中,平面
中,平面 平面
平面 ,
, ,
, ,
, ,D,E分别为
,D,E分别为 ,
, 的中点.
的中点.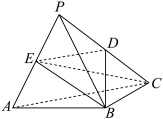
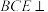 平面
平面 .
.(2)求平面
 与平面
与平面 的夹角的余弦值.
的夹角的余弦值.
您最近一年使用:0次
2023-12-23更新
|
1394次组卷
|
5卷引用:贵州省黔东南苗族侗族自治州2024届高三12月统测(一模)数学试题
名校
解题方法
2 . 如图,在四棱锥 中,底面
中,底面 为梯形,
为梯形, ,
, ,
, ,
,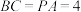 ,
,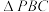 是等边三角形.
是等边三角形.

(1)证明:平面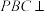 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
 中,底面
中,底面 为梯形,
为梯形, ,
, ,
, ,
,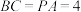 ,
,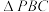 是等边三角形.
是等边三角形.
(1)证明:平面
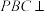 平面
平面 ;
;(2)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
您最近一年使用:0次
2023-07-25更新
|
440次组卷
|
2卷引用:贵州省贵阳市第一中学2023届高三上学期期末理科数学试题
名校
解题方法
3 . 如图,已知直角梯形 与
与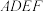 ,
, ,
, ,
, ,AD⊥AB,
,AD⊥AB,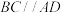 ,G是线段
,G是线段 上一点.
上一点.
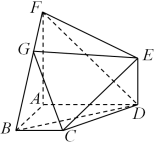
(1)平面 ⊥平面ABF
⊥平面ABF
(2)若平面 ⊥平面
⊥平面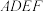 ,设平面
,设平面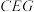 与平面
与平面 所成角为
所成角为 ,是否存在点G,使得
,是否存在点G,使得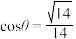 ,若存在确定G点位置;若不存在,请说明理由.
,若存在确定G点位置;若不存在,请说明理由.
 与
与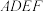 ,
, ,
, ,
, ,AD⊥AB,
,AD⊥AB,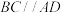 ,G是线段
,G是线段 上一点.
上一点.
(1)平面
 ⊥平面ABF
⊥平面ABF(2)若平面
 ⊥平面
⊥平面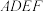 ,设平面
,设平面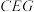 与平面
与平面 所成角为
所成角为 ,是否存在点G,使得
,是否存在点G,使得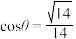 ,若存在确定G点位置;若不存在,请说明理由.
,若存在确定G点位置;若不存在,请说明理由.
您最近一年使用:0次
2023-07-21更新
|
1580次组卷
|
5卷引用:贵州省黔西南州兴义市顶效开发区顶兴学校2023-2024学年高三上学期第二次月考数学试题
名校
4 . 如图所示,在四棱锥 中,该四棱锥的底面
中,该四棱锥的底面 是边长为6的菱形,
是边长为6的菱形,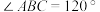 ,
,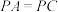 ,
,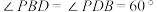 ,
, 为线段
为线段 上靠近
上靠近 点的三等分点.
点的三等分点. 平面
平面 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得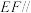 平面
平面 ?若存在,求
?若存在,求 的值及直线
的值及直线 与平面
与平面 所成角的大小;若不存在,请说明理由.
所成角的大小;若不存在,请说明理由.
 中,该四棱锥的底面
中,该四棱锥的底面 是边长为6的菱形,
是边长为6的菱形,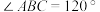 ,
,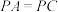 ,
,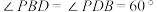 ,
, 为线段
为线段 上靠近
上靠近 点的三等分点.
点的三等分点.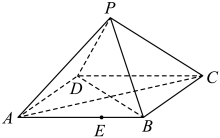
 平面
平面 ;
;(2)在线段
 上是否存在一点
上是否存在一点 ,使得
,使得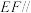 平面
平面 ?若存在,求
?若存在,求 的值及直线
的值及直线 与平面
与平面 所成角的大小;若不存在,请说明理由.
所成角的大小;若不存在,请说明理由.
您最近一年使用:0次
2023-07-17更新
|
837次组卷
|
4卷引用:贵州省安顺市2023-2024学年高一下学期6月质量检测数学试题
(已下线)贵州省安顺市2023-2024学年高一下学期6月质量检测数学试题云南省保山市文山州2022-2023学年高一下学期期末联合质量监测数学试题甘肃省张掖市某重点校2023-2024学年高二上学期开学(暑假学习效果)检测数学试题(已下线)第十一章:立体几何初步章末综合检测卷-同步精品课堂(人教B版2019必修第四册)
5 . 如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.

(1)证明:平面AMD⊥平面BMC;
(2)当三棱锥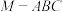 体积最大时,求面MAB与面MCD所成二面角的正切值.
体积最大时,求面MAB与面MCD所成二面角的正切值.

(1)证明:平面AMD⊥平面BMC;
(2)当三棱锥
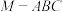 体积最大时,求面MAB与面MCD所成二面角的正切值.
体积最大时,求面MAB与面MCD所成二面角的正切值.
您最近一年使用:0次
2023-03-25更新
|
617次组卷
|
4卷引用:贵州省凯里市第一中学2022-2023学年高二下学期第一次月考数学试题
贵州省凯里市第一中学2022-2023学年高二下学期第一次月考数学试题四川省绵阳市南山中学2022-2023学年高二下学期期中考试数学(理)试题湖南省岳阳市平江县颐华高级中学2023-2024学年高三上学期入学考试数学试题(已下线)第6章 空间向量与立体几何 单元测试(B卷重难过关)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)
6 . 如图,在正三棱柱 中,
中,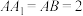 ,D,E分别是棱BC,
,D,E分别是棱BC, 的中点.
的中点.

(1)证明:平面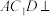 平面
平面 .
.
(2)求点 到平面
到平面 的距离.
的距离.
 中,
中,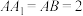 ,D,E分别是棱BC,
,D,E分别是棱BC, 的中点.
的中点.
(1)证明:平面
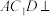 平面
平面 .
.(2)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2023-01-19更新
|
358次组卷
|
5卷引用:贵州省黔东南州2023届高三上学期复习统一检测(期末)数学(文)试题
贵州省黔东南州2023届高三上学期复习统一检测(期末)数学(文)试题江西省部分学校2023届高三上学期1月联考数学(文)试题(已下线)模块三 专题8(立体几何初步)拔高能力练(北师大版)(已下线)模块三 专题7 大题分类练(立体几何初步)拔高能力练(人教A)(已下线)模块三 专题8大题分类练(立体几何初步)拔高能力练(苏教版)
7 . 如图,在四棱锥 中,底面
中,底面 是边长为2的正方形,平面
是边长为2的正方形,平面 底面
底面 ,
,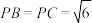 .
.

(1)证明:平面 平面
平面 ;
;
(2)已知点 是线段
是线段 的中点,求二面角
的中点,求二面角 的余弦值.
的余弦值.
 中,底面
中,底面 是边长为2的正方形,平面
是边长为2的正方形,平面 底面
底面 ,
,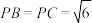 .
.
(1)证明:平面
 平面
平面 ;
;(2)已知点
 是线段
是线段 的中点,求二面角
的中点,求二面角 的余弦值.
的余弦值.
您最近一年使用:0次
名校
解题方法
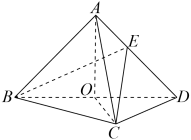
8 . 如图,在三棱锥 中,
中, ,且
,且 ,
, 为
为 的中点,点
的中点,点 在棱
在棱 上,
上,
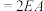 ,若
,若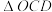 是边长为1的等边三角形,且
是边长为1的等边三角形,且 .
.
(1)证明:平面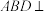 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,且
,且 ,
, 为
为 的中点,点
的中点,点 在棱
在棱 上,
上,
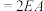 ,若
,若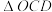 是边长为1的等边三角形,且
是边长为1的等边三角形,且 .
.
(1)证明:平面
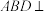 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2022-11-25更新
|
1125次组卷
|
3卷引用:贵州省贵阳市五校2023届高三上学期联合考试(三)数学(理)试题
9 . 如图,在三棱锥 是,
是, ,且
,且 ,O为
,O为 的中点,若
的中点,若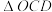 是边长为1的等边三角形,且
是边长为1的等边三角形,且 .
.
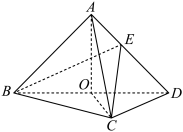
(1)证明:平面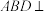 平面
平面 ;
;
(2)求点O到平面 的距离.
的距离.
 是,
是, ,且
,且 ,O为
,O为 的中点,若
的中点,若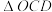 是边长为1的等边三角形,且
是边长为1的等边三角形,且 .
.
(1)证明:平面
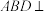 平面
平面 ;
;(2)求点O到平面
 的距离.
的距离.
您最近一年使用:0次
解题方法
10 . 如图,在正三棱柱 中,
中, ,
, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
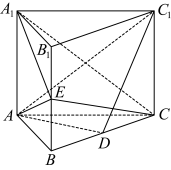
(1)证明:平面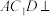 平面
平面 .
.
(2)求平面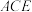 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中,
中, ,
, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)证明:平面
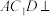 平面
平面 .
.(2)求平面
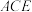 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
您最近一年使用:0次
2023-01-17更新
|
462次组卷
|
6卷引用:贵州省黔东南州2023届高三上学期复习统一检测(期末)数学(理)试题



