名校
解题方法
1 . 我国在2022年完成了天宫空间站的建设,根据开普勒第一定律,天宫空间站的运行轨道可以近似为椭圆,地球处于该椭圆的一个焦点上.已知某次变轨任务前后,天宫空间站的近地距离(天宫空间站与地球距离的最小值)不变,远地距离(天宫空间站与地球距离的最大值)扩大为变轨前的3倍,椭圆轨道的离心率扩大为变轨前的2倍,则此次变轨任务前的椭圆轨道的离心率为( )
A. | B.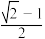 | C. | D.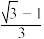 |
您最近半年使用:0次
2024-01-06更新
|
551次组卷
|
5卷引用:2023年普通高等学校招生“圆梦杯”统一模拟考试(三)数学试题
2023年普通高等学校招生“圆梦杯”统一模拟考试(三)数学试题北京市西城区2023-2024学年高二上学期期末模拟练习数学试题福建省莆田第一中学2023-2024学年高二上学期期末考试数学试题江西省上饶市广丰贞白中学2023-2024学年高二上学期1月考试数学试题(已下线)2.2.2 椭圆的性质(十八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
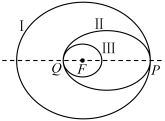
2 . 如图所示,“嫦娥五号”月球探测器飞行到月球附近时,首先在以月球球心 为圆心的圆形轨道I上绕月球飞行,然后在
为圆心的圆形轨道I上绕月球飞行,然后在 点处变轨进入以
点处变轨进入以 为一个焦点的椭圆轨道II绕月球飞行,最后在
为一个焦点的椭圆轨道II绕月球飞行,最后在 点处变轨进入以
点处变轨进入以 为圆心的圆形轨道III绕月球飞行,设圆形轨道I的半径为
为圆心的圆形轨道III绕月球飞行,设圆形轨道I的半径为 ,圆形轨道III的半径为
,圆形轨道III的半径为 ,则下列结论中正确的序号为( )
,则下列结论中正确的序号为( )
①轨道II的焦距为 ;
;
②若 不变,
不变, 越大,轨道II的短轴长越小;
越大,轨道II的短轴长越小;
③轨道II的长轴长为 ;
;
④若 不变,
不变, 越大,轨道II的离心率越大.
越大,轨道II的离心率越大.
 为圆心的圆形轨道I上绕月球飞行,然后在
为圆心的圆形轨道I上绕月球飞行,然后在 点处变轨进入以
点处变轨进入以 为一个焦点的椭圆轨道II绕月球飞行,最后在
为一个焦点的椭圆轨道II绕月球飞行,最后在 点处变轨进入以
点处变轨进入以 为圆心的圆形轨道III绕月球飞行,设圆形轨道I的半径为
为圆心的圆形轨道III绕月球飞行,设圆形轨道I的半径为 ,圆形轨道III的半径为
,圆形轨道III的半径为 ,则下列结论中正确的序号为( )
,则下列结论中正确的序号为( )
①轨道II的焦距为
 ;
;②若
 不变,
不变, 越大,轨道II的短轴长越小;
越大,轨道II的短轴长越小;③轨道II的长轴长为
 ;
;④若
 不变,
不变, 越大,轨道II的离心率越大.
越大,轨道II的离心率越大.| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
您最近半年使用:0次
2023-12-28更新
|
271次组卷
|
4卷引用:内蒙古锡林郭勒盟2024届高三上学期第二次统一考试(12月月考)(全国乙卷)理科数学试题
内蒙古锡林郭勒盟2024届高三上学期第二次统一考试(12月月考)(全国乙卷)理科数学试题内蒙古锡林郭勒盟2024届高三上学期第二次统一考试(12月月考)(全国乙卷)文科数学试题(已下线)专题11椭圆(3个知识点7个拓展2个突破7种题型2个易错点)-【倍速学习法】2023-2024学年高二数学核心知识点与常见题型通关讲解练(人教A版2019选修第一册)(已下线)2.2.2 椭圆的性质(十八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
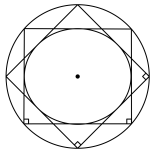
3 . 法国著名数学家加斯帕尔·蒙日在研究圆锥曲线时发现:椭圆 或
或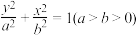 的任意两条互相垂直的切线的交点
的任意两条互相垂直的切线的交点 的轨迹是以坐标原点为圆心,
的轨迹是以坐标原点为圆心, 为半径的圆,这个圆称为蒙日圆.已知椭圆
为半径的圆,这个圆称为蒙日圆.已知椭圆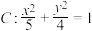 ,则下列说法正确的是( )
,则下列说法正确的是( )
 或
或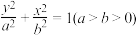 的任意两条互相垂直的切线的交点
的任意两条互相垂直的切线的交点 的轨迹是以坐标原点为圆心,
的轨迹是以坐标原点为圆心, 为半径的圆,这个圆称为蒙日圆.已知椭圆
为半径的圆,这个圆称为蒙日圆.已知椭圆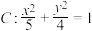 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.椭圆 的蒙日圆方程为 的蒙日圆方程为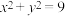 |
B.矩形 的四边均与椭圆 的四边均与椭圆 相切,若 相切,若 为正方形,则 为正方形,则 的边长为 的边长为 |
C.若 是椭圆 是椭圆 的蒙日圆上一个动点,过 的蒙日圆上一个动点,过 作椭圆 作椭圆 的两条切线,与该蒙日圆分别交于 的两条切线,与该蒙日圆分别交于 , , 两点,则 两点,则 面积的最大值为 面积的最大值为 |
D.若 是直线 是直线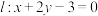 上的一点,过点 上的一点,过点 作椭圆 作椭圆 的两条切线与椭圆相切于 的两条切线与椭圆相切于 , , 两点, 两点, 是坐标原点,连接 是坐标原点,连接 ,当 ,当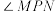 为直角时, 为直角时,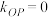 或 或 |
您最近半年使用:0次
2023-12-14更新
|
149次组卷
|
3卷引用:2024年全国高考名校名师联席命制型数学信息卷(四)
(已下线)2024年全国高考名校名师联席命制型数学信息卷(四)湖北省武汉市新洲区部分学校2023-2024学年高二上学期期中质量检测数学试题湖南省衡阳市衡阳县第二中学2023-2024学年高二上学期期末达标测试数学试题(B卷)
名校
4 . 古希腊数学家阿波罗尼奥斯所著的八册《圆锥曲线论(Conics)》中,首次提出了圆锥曲线的光学性质,其中之一的内容为:“若点 为椭圆上的一点,
为椭圆上的一点, 、
、 为椭圆的两个焦点,则点
为椭圆的两个焦点,则点 处的切线平分
处的切线平分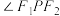 外角”.根据此信息回答下列问题:已知椭圆
外角”.根据此信息回答下列问题:已知椭圆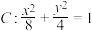 ,
, 为坐标原点,
为坐标原点, 是点
是点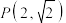 处的切线,过左焦点
处的切线,过左焦点 作
作 的垂线,垂足为
的垂线,垂足为 ,则
,则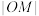 为( )
为( )
 为椭圆上的一点,
为椭圆上的一点, 、
、 为椭圆的两个焦点,则点
为椭圆的两个焦点,则点 处的切线平分
处的切线平分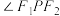 外角”.根据此信息回答下列问题:已知椭圆
外角”.根据此信息回答下列问题:已知椭圆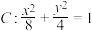 ,
, 为坐标原点,
为坐标原点, 是点
是点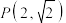 处的切线,过左焦点
处的切线,过左焦点 作
作 的垂线,垂足为
的垂线,垂足为 ,则
,则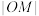 为( )
为( )A. | B. | C. | D. |
您最近半年使用:0次
2023-11-15更新
|
619次组卷
|
3卷引用:福建省厦门第一中学2024届高三上学期期中考试数学试题
22-23高二下·河北邯郸·期末
名校
5 . 开普勒第一定律也称椭圆定律、轨道定律,其内容如下:每一行星沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点上.将某行星 看作一个质点,
看作一个质点, 绕太阳的运动轨迹近似成曲线
绕太阳的运动轨迹近似成曲线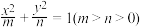 ,行星
,行星 在运动过程中距离太阳最近的距离称为近日点距离,距离太阳最远的距离称为远日点距离.若行星
在运动过程中距离太阳最近的距离称为近日点距离,距离太阳最远的距离称为远日点距离.若行星 的近日点距离和远日点距离之和是18(距离单位:亿千米),近日点距离和远日点距离之积是16,则
的近日点距离和远日点距离之和是18(距离单位:亿千米),近日点距离和远日点距离之积是16,则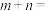 ( )
( )
 看作一个质点,
看作一个质点, 绕太阳的运动轨迹近似成曲线
绕太阳的运动轨迹近似成曲线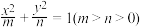 ,行星
,行星 在运动过程中距离太阳最近的距离称为近日点距离,距离太阳最远的距离称为远日点距离.若行星
在运动过程中距离太阳最近的距离称为近日点距离,距离太阳最远的距离称为远日点距离.若行星 的近日点距离和远日点距离之和是18(距离单位:亿千米),近日点距离和远日点距离之积是16,则
的近日点距离和远日点距离之和是18(距离单位:亿千米),近日点距离和远日点距离之积是16,则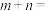 ( )
( )| A.39 | B.52 | C.86 | D.97 |
您最近半年使用:0次
2023-07-05更新
|
891次组卷
|
11卷引用:模块四 专题8 高考新题型(复杂情景题专训)基础夯实练(人教A)
(已下线)模块四 专题8 高考新题型(复杂情景题专训)基础夯实练(人教A)河北省邯郸市2022-2023学年高二下学期期末考试数学试题第三章 圆锥曲线的方程 讲核心03湖南省湘潭市湘潭县第一中学等2022-2023学年高二下学期期末联考数学试题(已下线)第20讲 椭圆的简单几何性质10种常见考法归类(2)(已下线)第02讲 3.1.2椭圆的简单几何性质(2)(已下线)3.1.2 椭圆的简单几何性质(精练)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)3.1.2 椭圆的几何性质(2)陕西省咸阳市高新一中2023-2024学年高二上学期期中考试数学试卷(已下线)专题06 椭圆的压轴题(6类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)(已下线)通关练15 椭圆11考点精练(3)
6 . 我国南北朝时期的伟大科学家祖暅于5世纪末提出了下面的体积计算原理:“幂势既同,则积不容异”.这就是“祖暅原理”.祖暅原理用现代语言可描述为:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.运用祖暅原理计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图1)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图2),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面的面积都相等,由此得到新几何体与半球的体积相等,即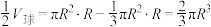 .现将椭圆
.现将椭圆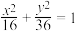 绕
绕 轴旋转一周后得到如图3所示的椭球,类比上述方法,运用祖暅原理可求得该椭球的体积为( )
轴旋转一周后得到如图3所示的椭球,类比上述方法,运用祖暅原理可求得该椭球的体积为( )

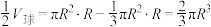 .现将椭圆
.现将椭圆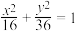 绕
绕 轴旋转一周后得到如图3所示的椭球,类比上述方法,运用祖暅原理可求得该椭球的体积为( )
轴旋转一周后得到如图3所示的椭球,类比上述方法,运用祖暅原理可求得该椭球的体积为( )
A. | B.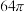 | C. | D. |
您最近半年使用:0次
解题方法
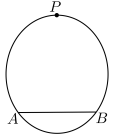
7 . 韶州大桥是一座独塔双索面钢砼混合梁斜拉桥,具有桩深,塔高、梁重、跨大的特点,它打通了曲江区、浈江区、武江区交通道路的瓶颈,成为连接曲江区与芙蓉新城的重要交通桥梁,大桥承担着实现韶关“三区融合”的重要使命,韶州大桥的桥塔外形近似椭圆,若桥塔所在平面截桥面为线段 ,且
,且 过椭圆的下焦点,
过椭圆的下焦点, 米,桥塔最高点
米,桥塔最高点 距桥面
距桥面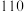 米,则此椭圆的离心率为( )
米,则此椭圆的离心率为( )

 ,且
,且 过椭圆的下焦点,
过椭圆的下焦点, 米,桥塔最高点
米,桥塔最高点 距桥面
距桥面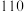 米,则此椭圆的离心率为( )
米,则此椭圆的离心率为( )

A. | B. | C. | D. |
您最近半年使用:0次
2023-05-29更新
|
918次组卷
|
9卷引用:广东省韶关市2023届高三下学期4月综合测试(二)数学试题
广东省韶关市2023届高三下学期4月综合测试(二)数学试题(已下线)模块四 专题8 高考新题型(复杂情景题专训)基础夯实练(人教A)(已下线)第20讲 椭圆的简单几何性质10种常见考法归类(2)(已下线)专题3.2 椭圆的简单几何性质【八大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)第02讲 3.1.2椭圆的简单几何性质(2)(已下线)3.1.2 椭圆的简单几何性质(精讲)-2023-2024学年高二数学《一隅三反》系列(人教A版2019选择性必修第一册)(已下线)第05讲 椭圆及其性质(练习)(已下线)3.1.2 椭圆的简单几何性质【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)2.2.2 椭圆的性质(十八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)
名校
8 . 中国国家大剧院的外观被设计成了半椭球面的形状.如图,若以椭球的中心为原点建立空间直角坐标系,半椭球面的方程为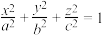 (
(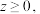 ,
, ,且a,b,c不全相等).若该建筑的室内地面是面积为
,且a,b,c不全相等).若该建筑的室内地面是面积为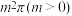 的圆,给出下列结论:①
的圆,给出下列结论:① ;②
;② ;③
;③ ;④若
;④若 ,则
,则 ,其中正确命题的个数为( )
,其中正确命题的个数为( )
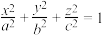 (
(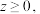 ,
, ,且a,b,c不全相等).若该建筑的室内地面是面积为
,且a,b,c不全相等).若该建筑的室内地面是面积为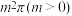 的圆,给出下列结论:①
的圆,给出下列结论:① ;②
;② ;③
;③ ;④若
;④若 ,则
,则 ,其中正确命题的个数为( )
,其中正确命题的个数为( )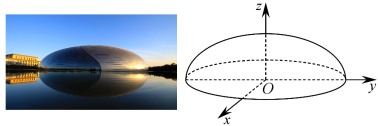
| A.1 | B.2 | C.3 | D.4 |
您最近半年使用:0次
2023-05-29更新
|
620次组卷
|
4卷引用:河北省部分学校2023届高三下学期第一次高考模拟演练数学试题
2022·江西九江·三模
名校
解题方法
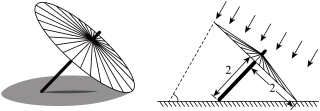
9 . 油纸伞是中国传统工艺品,至今已有1000多年的历史,为宣传和推广这一传统工艺,北京市文化宫开展油纸伞文化艺术节活动中,某油纸伞撑开后摆放在户外展览场地上,如图所示,该伞伞沿是一个半径为2的圆,圆心到伞柄底端距离为2,当阳光与地面夹角为 时,在地面形成了一个椭圆形影子,且伞柄底端正好位于该椭圆的长轴上,若该椭圆的离心率为e,则
时,在地面形成了一个椭圆形影子,且伞柄底端正好位于该椭圆的长轴上,若该椭圆的离心率为e,则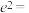 ( )
( )
 时,在地面形成了一个椭圆形影子,且伞柄底端正好位于该椭圆的长轴上,若该椭圆的离心率为e,则
时,在地面形成了一个椭圆形影子,且伞柄底端正好位于该椭圆的长轴上,若该椭圆的离心率为e,则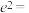 ( )
( )
A.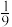 | B. | C.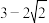 | D.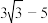 |
您最近半年使用:0次
2023-10-19更新
|
1418次组卷
|
13卷引用:专题20 椭圆-2
(已下线)专题20 椭圆-2江西省九江市2022届第三次高考模拟统一考试数学(理)试题(已下线)第三章 圆锥曲线的方程(单元测试)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第一册)江苏省南京市第五高级中学2023-2024学年高二上学期10月月考数学试题辽宁省沈阳市东北育才双语学校2023-2024学年高二上学期期中数学试题陕西省西安市陕西师大附中2023-2024学年高二上学期期中数学试题重庆市第十八中学2023-2024学年高二上学期期中学习能力摸底数学试题重庆市黔江中学校2023-2024学年高二上学期11月考试数学试题(已下线)黄金卷05湖南省常德市临澧县第一中学2023-2024学年高二下学期入学考试数学试题安徽省淮北市国泰中学2023-2024学年高二上学期期末考试数学试题(已下线)2.2.2 椭圆的性质(十八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020选择性必修第一册)上海市上海中学东校2023-2024学年高二下学期期中考试数学试卷
2023高三·全国·专题练习
10 . 已知椭圆C: 上、下顶点分别为
上、下顶点分别为 ,且短轴长为
,且短轴长为 ,T为椭圆上(除
,T为椭圆上(除 外)任意一点,直线
外)任意一点,直线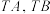 的斜率之积为
的斜率之积为 ,
, ,
, 分别为左、右焦点.
分别为左、右焦点.
(1)求椭圆C的方程.
(2)“天眼”是世界上最大、最灵敏的单口径射电望远镜,它的外形像一口“大锅”,可以接收到百亿光年外的电磁信号.在“天眼”的建设中,用到了大量的圆锥曲线的光学性质,请以上面的椭圆C为代表,证明:由焦点 发出的光线射到椭圆上任意一点M后反射,反射光线必经过另一焦点
发出的光线射到椭圆上任意一点M后反射,反射光线必经过另一焦点 .(提示:光线射到曲线上某点并反射时,法线垂直于该点处的切线)
.(提示:光线射到曲线上某点并反射时,法线垂直于该点处的切线)
 上、下顶点分别为
上、下顶点分别为 ,且短轴长为
,且短轴长为 ,T为椭圆上(除
,T为椭圆上(除 外)任意一点,直线
外)任意一点,直线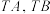 的斜率之积为
的斜率之积为 ,
, ,
, 分别为左、右焦点.
分别为左、右焦点.(1)求椭圆C的方程.
(2)“天眼”是世界上最大、最灵敏的单口径射电望远镜,它的外形像一口“大锅”,可以接收到百亿光年外的电磁信号.在“天眼”的建设中,用到了大量的圆锥曲线的光学性质,请以上面的椭圆C为代表,证明:由焦点
 发出的光线射到椭圆上任意一点M后反射,反射光线必经过另一焦点
发出的光线射到椭圆上任意一点M后反射,反射光线必经过另一焦点 .(提示:光线射到曲线上某点并反射时,法线垂直于该点处的切线)
.(提示:光线射到曲线上某点并反射时,法线垂直于该点处的切线)
您最近半年使用:0次



