解题方法
1 . 已知抛物线: ,焦点为F,
,焦点为F,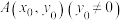 为
为 上的一个动点,
上的一个动点, 是
是 在点A处的切线,点P在
在点A处的切线,点P在 上且与点A不重合.直线PF与Γ交于B、C两点,且
上且与点A不重合.直线PF与Γ交于B、C两点,且 平分直线AB和直线AC的夹角.
平分直线AB和直线AC的夹角.
(1)求 的方程(用
的方程(用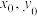 表示);
表示);
(2)若从点F发出的光线经过点A反射,证明:反射光线平行于x轴;
(3)若点A坐标为 ,求点P坐标.
,求点P坐标.
 ,焦点为F,
,焦点为F,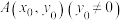 为
为 上的一个动点,
上的一个动点, 是
是 在点A处的切线,点P在
在点A处的切线,点P在 上且与点A不重合.直线PF与Γ交于B、C两点,且
上且与点A不重合.直线PF与Γ交于B、C两点,且 平分直线AB和直线AC的夹角.
平分直线AB和直线AC的夹角.(1)求
 的方程(用
的方程(用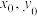 表示);
表示);(2)若从点F发出的光线经过点A反射,证明:反射光线平行于x轴;
(3)若点A坐标为
 ,求点P坐标.
,求点P坐标.
您最近一年使用:0次
2024-05-16更新
|
447次组卷
|
2卷引用:上海市桃浦中学2024届高三三模模拟数学试题
名校
解题方法
2 . 若P,Q分别是抛物线 与圆
与圆 上的点,则
上的点,则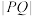 的最小值为
的最小值为________ .
 与圆
与圆 上的点,则
上的点,则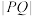 的最小值为
的最小值为
您最近一年使用:0次
2023-02-23更新
|
6219次组卷
|
17卷引用:上海市嘉定区第二中学2023届高三三模数学试题
上海市嘉定区第二中学2023届高三三模数学试题2023届安徽省、云南省、吉林省、黑龙江省高三下学期2月适应性测试数学试题云南省2023届高三第一次高中毕业生复习统一检测数学试题山西省大同市2023届高三阶段性模拟(2月联考)数学试题(A卷)上海市延安中学2022-2023学年高二下学期期中数学试题陕西省宝鸡市千阳县中学2023届高三第十二次模考理科数学试题陕西省宝鸡市千阳县中学2023届高三第十二次模考文科数学试题 陕西省咸阳市兴平市南郊高级中学2022-2023学年高三下学期三模理科数学试题上海市向明中学2022-2023学年高二下学期期中数学试题山西省大同市第一中学校等2校2023届高三一模理科数学试题2023年安徽省、云南省、吉林省、黑龙江省联考数学试卷评价(已下线)2023年四省联考变试题11-16(已下线)专题22 抛物线-2江西省宜春市丰城市第九中学2022-2023学年高二下学期第一次段考(3月)数学试题(已下线)江西省九师联盟2024届高三上学期10月联考数学试题安徽省马鞍山市第二中学2023-2024学年高二下学期阶段性检测数学试题湖北省武汉市第七中学2023-2024学年高二下学期3月月考数学试卷
名校
解题方法
3 . 抛物线 的焦点为
的焦点为 ,点
,点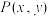 为该抛物线上的动点,又点
为该抛物线上的动点,又点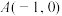 ,则
,则 的最小值是( )
的最小值是( )
 的焦点为
的焦点为 ,点
,点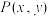 为该抛物线上的动点,又点
为该抛物线上的动点,又点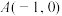 ,则
,则 的最小值是( )
的最小值是( )A. | B. | C. | D. |
您最近一年使用:0次
2023-01-12更新
|
851次组卷
|
12卷引用:2016届上海市浦东新区高三4月高考模拟(二模)数学试题
2016届上海市浦东新区高三4月高考模拟(二模)数学试题2019届陕西省渭南市高三第二次教学质量检测数学(理)试题2019届陕西省渭南市高三第二次教学质量检测数学(文)试题上海市高桥中学2022届高三上学期9月月考数学试题(已下线)上海市华东师范大学第二附属中学2022-2023学年高二下学期期末数学试题河南省信阳市新县高级中学2023届高三第一轮适应性考试(二)数学(理科)试题上海市南洋中学2023-2024学年高二下学期期末数学试题江苏省南通市如东高级中学、栟茶中学等四校2019-2020学年高二上学期期中数学试题北京名校2023届高三二轮复习 专题五 解析几何 第2讲 圆锥曲线北京市朝阳区北京中学2023-2024高二上学期12月月考数学试题北京市海淀区中关村中学2024届高三上学期12月月考数学试题(已下线)模块二 专题2 解析几何中最值问题
4 . 已知抛物线 的焦点为F,准线为l;
的焦点为F,准线为l;
(1)若F为双曲线 的一个焦点,求双曲线C的离心率e;
的一个焦点,求双曲线C的离心率e;
(2)设l与x轴的交点为E,点P在第一象限,且在 上,若
上,若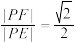 ,求直线EP的方程;
,求直线EP的方程;
(3)经过点F且斜率为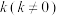 的直线l'与
的直线l'与 相交于A,B两点,O为坐标原点,直线
相交于A,B两点,O为坐标原点,直线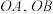 分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
 的焦点为F,准线为l;
的焦点为F,准线为l;(1)若F为双曲线
 的一个焦点,求双曲线C的离心率e;
的一个焦点,求双曲线C的离心率e;(2)设l与x轴的交点为E,点P在第一象限,且在
 上,若
上,若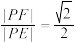 ,求直线EP的方程;
,求直线EP的方程;(3)经过点F且斜率为
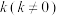 的直线l'与
的直线l'与 相交于A,B两点,O为坐标原点,直线
相交于A,B两点,O为坐标原点,直线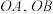 分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
您最近一年使用:0次
2022-12-15更新
|
1022次组卷
|
4卷引用:上海市长宁区2023届高三上学期一模数学试题
上海市长宁区2023届高三上学期一模数学试题上海市奉贤区致远高级中学2022-2023学年高二下学期3月教学评估数学试题上海市复兴高级中学2024届高三上学期开学考试数学试题(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)
名校
5 . 《九章算术》是我国古代内容极为丰富的数学著作,第九章“勾股”讲述了勾股定理及一些应用,将直角三角形的斜边称为“弦”,短直角边称为“勾”,长直角边称为“股”,设点F是抛物线 的焦点.l是该抛物线的准线,过抛物线上一点A作准线的垂线AB,垂足为B,射线AF交准线l于点C,若
的焦点.l是该抛物线的准线,过抛物线上一点A作准线的垂线AB,垂足为B,射线AF交准线l于点C,若 的“勾”
的“勾” ,“股”
,“股”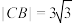 ,则抛物线的方程为
,则抛物线的方程为__ .
 的焦点.l是该抛物线的准线,过抛物线上一点A作准线的垂线AB,垂足为B,射线AF交准线l于点C,若
的焦点.l是该抛物线的准线,过抛物线上一点A作准线的垂线AB,垂足为B,射线AF交准线l于点C,若 的“勾”
的“勾” ,“股”
,“股”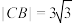 ,则抛物线的方程为
,则抛物线的方程为
您最近一年使用:0次
2022-10-16更新
|
1544次组卷
|
7卷引用:上海市徐汇区2022届高三下学期二模数学试题
上海市徐汇区2022届高三下学期二模数学试题(已下线)第15讲 抛物线-2(已下线)第07讲 抛物线 (高频考点,精练)(已下线)数学(新高考Ⅰ卷B卷)(已下线)专题20 抛物线的焦点弦问题四川省达州市宣汉中学2022-2023学年高二下学期入学考试理科数学试题(已下线)3.3.1 抛物线及其标准方程——课后作业(巩固版)
6 . 已知点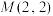 ,直线
,直线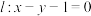 ,若动点
,若动点 到
到 的距离等于
的距离等于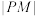 ,则点
,则点 的轨迹是( )
的轨迹是( )
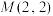 ,直线
,直线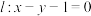 ,若动点
,若动点 到
到 的距离等于
的距离等于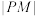 ,则点
,则点 的轨迹是( )
的轨迹是( )| A.椭圆 | B.双曲线 |
| C.抛物线 | D.直线 |
您最近一年使用:0次
名校
解题方法
7 . 已知双曲线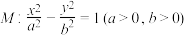 的一条渐近线与抛物线
的一条渐近线与抛物线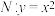 的一个交点为
的一个交点为 ,且点
,且点 到抛物线
到抛物线 的焦点的距离为
的焦点的距离为 ,则双曲线
,则双曲线 的离心率为( )
的离心率为( )
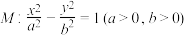 的一条渐近线与抛物线
的一条渐近线与抛物线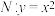 的一个交点为
的一个交点为 ,且点
,且点 到抛物线
到抛物线 的焦点的距离为
的焦点的距离为 ,则双曲线
,则双曲线 的离心率为( )
的离心率为( )A. | B.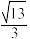 | C.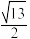 | D. |
您最近一年使用:0次
2022-04-20更新
|
822次组卷
|
5卷引用:上海市曹杨第二中学2023届高三上学期高考模拟(11月)数学试题
名校
8 . 若抛物线 上一点
上一点 到
到 轴的距离是4,则点
轴的距离是4,则点 到该抛物线焦点的距离是
到该抛物线焦点的距离是___________ .
 上一点
上一点 到
到 轴的距离是4,则点
轴的距离是4,则点 到该抛物线焦点的距离是
到该抛物线焦点的距离是
您最近一年使用:0次
2021-12-24更新
|
864次组卷
|
5卷引用:上海市松江区2022届高三一模数学试题
上海市松江区2022届高三一模数学试题浙江省湖州市2021-2022学年高二上学期期末数学试题北京海淀实验中学2021-2022学年高二数学期末试题(已下线)热点11 圆锥曲线的定义方程与性质【热点·重点·难点】专练(全国通用)(已下线)江苏省南京市某校2023-2024学年高二下学期5月阶段检测数学试题
9 . 如图,某飞行器研究基地E在指挥中心F的正北方向4千米处,小镇A在E的正西方向8千米处,小镇B在F的正南方向8千米处.已知一新型飞行器在试飞过程中到点F和到直线AE的距离始终相等,该飞行器产生一定的噪音污染,距离该飞行器1千米以内(含边界)为10级噪音,每远离飞行器1千米,噪音污染就会减弱1级,直至0级为无噪音污染(飞行器的大小及高度均忽略不计).
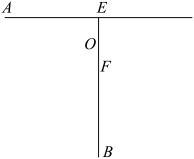
(1)判断该飞行器是否经过线段EF的中点O,并判断小镇A是否会受到该飞行器的噪音污染?
(2)小镇B受该飞行器噪音污染的最强等级为多少级?

(1)判断该飞行器是否经过线段EF的中点O,并判断小镇A是否会受到该飞行器的噪音污染?
(2)小镇B受该飞行器噪音污染的最强等级为多少级?
您最近一年使用:0次
2021-12-20更新
|
423次组卷
|
2卷引用:上海市闵行区2022届高三上学期一模数学试题
名校
解题方法
10 . 设常数 .在平面直角坐标系xOy中,已知点F(2,0),直线l:x=t,曲线
.在平面直角坐标系xOy中,已知点F(2,0),直线l:x=t,曲线 :
: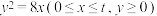 ,
, 与x轴交于点A、与
与x轴交于点A、与 交于点B.P、Q分别是曲线
交于点B.P、Q分别是曲线 与线段AB上的动点.
与线段AB上的动点.
(1)用t表示点B到点F距离;
(2)设 ,
,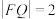 ,线段OQ的中点在直线FP上,求
,线段OQ的中点在直线FP上,求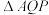 的面积;
的面积;
(3)设t=8,是否存在以FP、FQ为邻边的矩形FPEQ,使得点E在 上?若存在,求点P的坐标;若不存在,说明理由.
上?若存在,求点P的坐标;若不存在,说明理由.
 .在平面直角坐标系xOy中,已知点F(2,0),直线l:x=t,曲线
.在平面直角坐标系xOy中,已知点F(2,0),直线l:x=t,曲线 :
: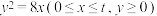 ,
, 与x轴交于点A、与
与x轴交于点A、与 交于点B.P、Q分别是曲线
交于点B.P、Q分别是曲线 与线段AB上的动点.
与线段AB上的动点.(1)用t表示点B到点F距离;
(2)设
 ,
,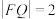 ,线段OQ的中点在直线FP上,求
,线段OQ的中点在直线FP上,求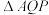 的面积;
的面积;(3)设t=8,是否存在以FP、FQ为邻边的矩形FPEQ,使得点E在
 上?若存在,求点P的坐标;若不存在,说明理由.
上?若存在,求点P的坐标;若不存在,说明理由.
您最近一年使用:0次
2021-04-16更新
|
1986次组卷
|
21卷引用:上海市复旦大学附属中学2019届高三高考4月模拟试卷数学试题
上海市复旦大学附属中学2019届高三高考4月模拟试卷数学试题2018年全国普通高等学校招生统一考试数学(上海卷)【全国百强校】河北省衡水中学2019届高三上学期四调考试数学(文)试题【全国百强校】江西省新余四中、上高二中2019届高三第二次联考数学(理)试题上海市同济大学第一附属中学2022-2023学年高二下学期期中数学试题【课后练】2.4.2.1抛物线的性质 课后作业-沪教版(2020)选择性必修第一册第2章 圆锥曲线上海市川沙中学2024-2025学年高三上学期期中考试数学试卷(已下线)专题29 圆锥曲线的综合问题-十年(2011-2020)高考真题数学分项(已下线)专题13 解析几何中的范围、最值和探索性问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)重组卷02-冲刺2021年高考数学之精选真题+模拟重组卷(新高考地区专用)(已下线) 专题22 圆锥曲线的“三定”与探索性问题(练)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题26 圆锥曲线的“三定”与探索性问题(练)-2021年高三数学二轮复习讲练测( 文理通用)(已下线)专题11 圆锥曲线-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)专题2.11 圆锥曲线-定点、定值、定直线问题-2021年高考数学解答题挑战满分专项训练(新高考地区专用)人教B版(2019) 选修第一册 过关检测 第二章 专项把关练沪教版(2020) 选修第一册 同步跟踪练习 期中测试卷(已下线)专题24 圆锥曲线中的存在性、探索性问题 微点3 圆锥曲线中的存在性、探索性问题综合训练(已下线)第15讲 抛物线-2(已下线)专题9.9 圆锥曲线的综合问题(练)-浙江版《2020年高考一轮复习讲练测》(已下线)专题24 解析几何解答题(文科)-2(已下线)专题24 解析几何解答题(理科)-3



