名校
解题方法
1 . 在平面直角坐标系 中,抛物线
中,抛物线 的焦点到准线的距离等于椭圆
的焦点到准线的距离等于椭圆 的短轴长,点
的短轴长,点 在抛物线
在抛物线 上,圆
上,圆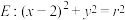 (其中
(其中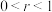 ).
).
(1)若 为圆
为圆 上的动点,求线段
上的动点,求线段 长度的最小值;
长度的最小值;
(2)设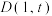 是抛物线
是抛物线 上位于第一象限的一点,过
上位于第一象限的一点,过 作圆
作圆 的两条切线,分别交抛物线
的两条切线,分别交抛物线 于点
于点 .证明:直线
.证明:直线 经过定点.
经过定点.
 中,抛物线
中,抛物线 的焦点到准线的距离等于椭圆
的焦点到准线的距离等于椭圆 的短轴长,点
的短轴长,点 在抛物线
在抛物线 上,圆
上,圆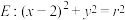 (其中
(其中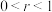 ).
).(1)若
 为圆
为圆 上的动点,求线段
上的动点,求线段 长度的最小值;
长度的最小值;(2)设
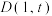 是抛物线
是抛物线 上位于第一象限的一点,过
上位于第一象限的一点,过 作圆
作圆 的两条切线,分别交抛物线
的两条切线,分别交抛物线 于点
于点 .证明:直线
.证明:直线 经过定点.
经过定点.
您最近一年使用:0次
名校
解题方法
2 . 已知抛物线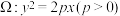 的焦点为
的焦点为 .过F作两条互相垂直的直线
.过F作两条互相垂直的直线 ,
, ,且直线
,且直线 与
与 交于M,N两点,直线
交于M,N两点,直线 与
与 交于E,P两点,M,E均在第一象限.设A,B分别为弦MN,EP的中点,直线ME与直线NP交于点H.
交于E,P两点,M,E均在第一象限.设A,B分别为弦MN,EP的中点,直线ME与直线NP交于点H.
(1)求 的方程.
的方程.
(2)直线AB是否过定点?若是,求出定点坐标;若不是,请说明理由.
(3)证明:点H在直线 上.
上.
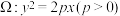 的焦点为
的焦点为 .过F作两条互相垂直的直线
.过F作两条互相垂直的直线 ,
, ,且直线
,且直线 与
与 交于M,N两点,直线
交于M,N两点,直线 与
与 交于E,P两点,M,E均在第一象限.设A,B分别为弦MN,EP的中点,直线ME与直线NP交于点H.
交于E,P两点,M,E均在第一象限.设A,B分别为弦MN,EP的中点,直线ME与直线NP交于点H.(1)求
 的方程.
的方程.(2)直线AB是否过定点?若是,求出定点坐标;若不是,请说明理由.
(3)证明:点H在直线
 上.
上.
您最近一年使用:0次
3 . 抛物线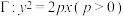 的图象经过点
的图象经过点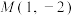 ,焦点为
,焦点为 ,过点
,过点 且倾斜角为
且倾斜角为 的直线
的直线 与抛物线
与抛物线 交于点
交于点 ,
, ,如图.
,如图. 的标准方程;
的标准方程;
(2)当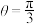 时,求弦
时,求弦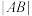 的长;
的长;
(3)已知点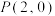 ,直线
,直线 ,
, 分别与抛物线
分别与抛物线 交于点
交于点 ,
, .证明:直线
.证明:直线 过定点.
过定点.
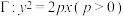 的图象经过点
的图象经过点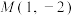 ,焦点为
,焦点为 ,过点
,过点 且倾斜角为
且倾斜角为 的直线
的直线 与抛物线
与抛物线 交于点
交于点 ,
, ,如图.
,如图.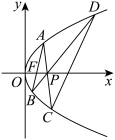
 的标准方程;
的标准方程;(2)当
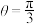 时,求弦
时,求弦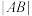 的长;
的长;(3)已知点
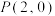 ,直线
,直线 ,
, 分别与抛物线
分别与抛物线 交于点
交于点 ,
, .证明:直线
.证明:直线 过定点.
过定点.
您最近一年使用:0次
2024-08-20更新
|
1168次组卷
|
5卷引用:9.4 点差法与定值、定点和最值(讲义)
(已下线)9.4 点差法与定值、定点和最值(讲义)(已下线)专题1 特殊探路 直接求解(经典好题母题)【练】云南省三校2025届高三高考备考实用性联考卷(二)福建省漳州市华安县第一中学2025届高三上学期开学模拟考试数学试题福建省福州市金山中学2025届高三上学期十月质量检测数学试卷
解题方法
4 . 在平面直角坐标系 中,顶点在原点
中,顶点在原点 的抛物线
的抛物线 经过点
经过点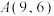 .
.
(1)求抛物线 的方程;
的方程;
(2)若抛物线 不经过第二象限,且经过点
不经过第二象限,且经过点 的直线
的直线 交抛物线
交抛物线 于
于 ,
, ,两点(
,两点(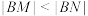 ),过
),过 作
作 轴的垂线交线段
轴的垂线交线段 于点
于点 .
.
①当 经过抛物线
经过抛物线 的焦点
的焦点 时,求直线
时,求直线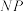 的方程;
的方程;
②求点A到直线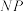 的距离的最大值.
的距离的最大值.
 中,顶点在原点
中,顶点在原点 的抛物线
的抛物线 经过点
经过点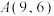 .
.(1)求抛物线
 的方程;
的方程;(2)若抛物线
 不经过第二象限,且经过点
不经过第二象限,且经过点 的直线
的直线 交抛物线
交抛物线 于
于 ,
, ,两点(
,两点(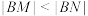 ),过
),过 作
作 轴的垂线交线段
轴的垂线交线段 于点
于点 .
.①当
 经过抛物线
经过抛物线 的焦点
的焦点 时,求直线
时,求直线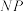 的方程;
的方程;②求点A到直线
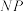 的距离的最大值.
的距离的最大值.
您最近一年使用:0次
2024-08-06更新
|
424次组卷
|
3卷引用:第07讲 抛物线及其性质(八大题型)(练习)
解题方法
5 . 已知 是抛物线
是抛物线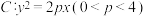 的焦点,纵坐标为
的焦点,纵坐标为 的点
的点 在
在 上,且
上,且 ,
, 是
是 上两点,直线
上两点,直线 不与
不与 轴垂直,且直线
轴垂直,且直线 关于
关于 轴对称.
轴对称.
(1)求 的方程;
的方程;
(2)求证:直线 过定点;
过定点;
(3)求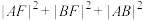 的取值范围.
的取值范围.
 是抛物线
是抛物线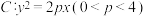 的焦点,纵坐标为
的焦点,纵坐标为 的点
的点 在
在 上,且
上,且 ,
, 是
是 上两点,直线
上两点,直线 不与
不与 轴垂直,且直线
轴垂直,且直线 关于
关于 轴对称.
轴对称.(1)求
 的方程;
的方程;(2)求证:直线
 过定点;
过定点;(3)求
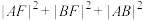 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-03更新
|
500次组卷
|
5卷引用:专题13 圆锥曲线中的齐次化(高三压轴题)【练】
(已下线)专题13 圆锥曲线中的齐次化(高三压轴题)【练】(已下线)压轴题08 圆锥曲线综合的5大常考类型-【常考压轴题】(人教B版2019选择性必修第一册)(已下线)专题3 圆锥曲线中的最值与范围问题【讲】(高二期中压轴专项)河南省商丘市部分学校2023-2024学年高二下学期期末考试数学试卷河南省林州市2023-2024学年高二下学期期末考试数学试卷
6 . 已知点 在抛物线
在抛物线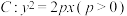 上,
上, 为抛物线
为抛物线 上两个动点,
上两个动点, 不垂直
不垂直 轴,
轴, 为焦点,且满足
为焦点,且满足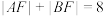 .
.
(1)求 的值及
的值及 的方程;
的方程;
(2)证明:线段 的垂直平分线过定点;
的垂直平分线过定点;
(3)设(1)中定点为 ,当
,当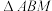 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
 在抛物线
在抛物线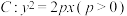 上,
上, 为抛物线
为抛物线 上两个动点,
上两个动点, 不垂直
不垂直 轴,
轴, 为焦点,且满足
为焦点,且满足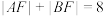 .
.(1)求
 的值及
的值及 的方程;
的方程;(2)证明:线段
 的垂直平分线过定点;
的垂直平分线过定点;(3)设(1)中定点为
 ,当
,当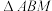 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
您最近一年使用:0次
2024-07-03更新
|
1224次组卷
|
4卷引用:抛物线02-一轮复习考点专练
7 . 已知抛物线 的焦点为
的焦点为 ,过
,过 的直线
的直线 交
交 于
于 两点,过
两点,过 与
与 垂直的直线交
垂直的直线交 于
于 两点,其中
两点,其中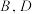 在
在 轴上方,
轴上方, 分别为
分别为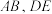 的中点.
的中点.
(1)证明:直线 过定点;
过定点;
(2)设 为直线
为直线 与直线
与直线 的交点,求
的交点,求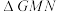 面积的最小值.
面积的最小值.
 的焦点为
的焦点为 ,过
,过 的直线
的直线 交
交 于
于 两点,过
两点,过 与
与 垂直的直线交
垂直的直线交 于
于 两点,其中
两点,其中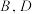 在
在 轴上方,
轴上方, 分别为
分别为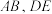 的中点.
的中点.(1)证明:直线
 过定点;
过定点;(2)设
 为直线
为直线 与直线
与直线 的交点,求
的交点,求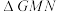 面积的最小值.
面积的最小值.
您最近一年使用:0次
2024-05-08更新
|
735次组卷
|
10卷引用:2024年1月普通高等学校招生全国统一考试适应性测试(九省联考)数学试题变式题16-19
(已下线)2024年1月普通高等学校招生全国统一考试适应性测试(九省联考)数学试题变式题16-192024年九省联考试卷分析及真题鉴赏(已下线)专题18 圆锥曲线高频压轴解答题(16大题型)(练习)(已下线)专题07 双曲线与抛物线(分层练)(五大题型+12道精选真题)(已下线)专题08 圆锥曲线 第二讲 圆锥曲线中的定点、定直线与定值问题(解密讲义)(已下线)9.3 抛物线(讲义)2024年1月普通高等学校招生全国统一考试适应性测试(九省联考)数学试题广东省惠州市第一中学2024届高三上学期第三次阶段测试数学试题福建省厦门双十中学2023-2024学年高二下学期开学考试数学试题四川省绵阳中学2024届高三下学期高考模拟(一)理科数学试题
名校
解题方法
8 . 在平面直角坐标系中,动点 到
到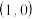 的距离等于到直线
的距离等于到直线 的距离.
的距离.
(1)求M的轨迹方程;
(2)P为不在x轴上的动点,过点 作(1)中
作(1)中 的轨迹的两条切线,切点为A,B;直线AB与PO垂直(O为坐标原点),与x轴的交点为R,与PO的交点为Q;
的轨迹的两条切线,切点为A,B;直线AB与PO垂直(O为坐标原点),与x轴的交点为R,与PO的交点为Q;
(ⅰ)求证:R是一个定点;
(ⅱ)求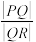 的最小值.
的最小值.
 到
到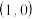 的距离等于到直线
的距离等于到直线 的距离.
的距离.(1)求M的轨迹方程;
(2)P为不在x轴上的动点,过点
 作(1)中
作(1)中 的轨迹的两条切线,切点为A,B;直线AB与PO垂直(O为坐标原点),与x轴的交点为R,与PO的交点为Q;
的轨迹的两条切线,切点为A,B;直线AB与PO垂直(O为坐标原点),与x轴的交点为R,与PO的交点为Q;(ⅰ)求证:R是一个定点;
(ⅱ)求
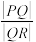 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
9 . 在平面直角坐标系 中,动点
中,动点 在抛物线
在抛物线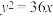 上运动,点
上运动,点 在
在 轴上的射影为
轴上的射影为 ,动点
,动点 满足
满足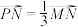 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点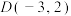 作直线与曲线
作直线与曲线 顺次交于
顺次交于 、
、 两点,过点
两点,过点 作斜率为1的直线与曲线
作斜率为1的直线与曲线 的另一个交点为点
的另一个交点为点 ,求证:直线
,求证:直线 过定点.
过定点.
 中,动点
中,动点 在抛物线
在抛物线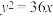 上运动,点
上运动,点 在
在 轴上的射影为
轴上的射影为 ,动点
,动点 满足
满足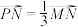 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过点
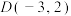 作直线与曲线
作直线与曲线 顺次交于
顺次交于 、
、 两点,过点
两点,过点 作斜率为1的直线与曲线
作斜率为1的直线与曲线 的另一个交点为点
的另一个交点为点 ,求证:直线
,求证:直线 过定点.
过定点.
您最近一年使用:0次
2024-09-01更新
|
500次组卷
|
3卷引用:模块二 专题2 解析几何中定值、定点、定直线问题【讲】(高二期中压轴专项)
解题方法
10 . 已知抛物线 的焦点
的焦点 到点
到点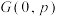 的距离为
的距离为 ,直线
,直线 经过点
经过点 ,且与
,且与 交于点
交于点 (
( 位于第一象限),
位于第一象限), 为抛物线上
为抛物线上 之间的一点,
之间的一点, 为点
为点 关于
关于 轴的对称点,则下列说法正确的是( )
轴的对称点,则下列说法正确的是( )
 的焦点
的焦点 到点
到点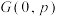 的距离为
的距离为 ,直线
,直线 经过点
经过点 ,且与
,且与 交于点
交于点 (
( 位于第一象限),
位于第一象限), 为抛物线上
为抛物线上 之间的一点,
之间的一点, 为点
为点 关于
关于 轴的对称点,则下列说法正确的是( )
轴的对称点,则下列说法正确的是( )A. |
B.若 的斜率为1,则当 的斜率为1,则当 到 到 的距离最大时, 的距离最大时,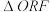 ( ( 为坐标原点)为直角三角形 为坐标原点)为直角三角形 |
C.若 ,则 ,则 的斜率为3 的斜率为3 |
D.若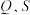 不重合,则直线 不重合,则直线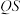 经过定点 经过定点 |
您最近一年使用:0次



