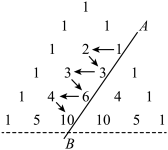
1 . 如图所示,在杨辉三角中,斜线 上方箭头所示的数组成一个锯齿形的数列:
上方箭头所示的数组成一个锯齿形的数列: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 记这个数列前
记这个数列前 项和为
项和为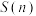 ,则
,则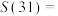
__________ .
 上方箭头所示的数组成一个锯齿形的数列:
上方箭头所示的数组成一个锯齿形的数列: ,
, ,
, ,
, ,
, ,
, ,
, ,
, 记这个数列前
记这个数列前 项和为
项和为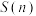 ,则
,则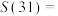

您最近半年使用:0次
2023-08-01更新
|
262次组卷
|
3卷引用:安徽省滁州市定远县育才学校2022-2023学年高二下学期期末考试数学试卷
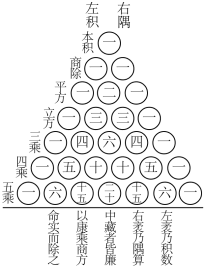
2 . “杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的第3个数6为第3行中两个3的和.记“杨辉三角”第 行的第
行的第 个数为
个数为 ,请用组合数第
,请用组合数第 行写出
行写出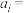
______ ,则
______ .
 行的第
行的第 个数为
个数为 ,请用组合数第
,请用组合数第 行写出
行写出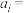


您最近半年使用:0次
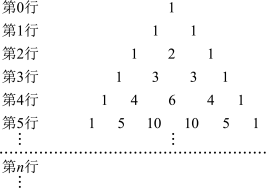
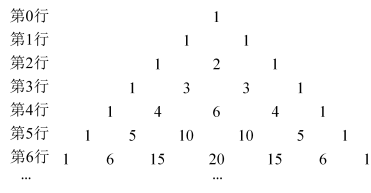
3 . 在“杨辉三角”中,每一个数都是它“肩上”两个数的和,它开头几行如图所示.那么,在“杨辉三角”中,第__________ 行会出现三个相邻的数,其比为 .
.
第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
 .
.第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
您最近半年使用:0次
2023-12-14更新
|
594次组卷
|
4卷引用:辽宁省本溪市第一中学2021-2022学年高二上学期期末数学试题
辽宁省本溪市第一中学2021-2022学年高二上学期期末数学试题(已下线)第六章 计数原理(知识归纳+题型突破)(4)(已下线)第7章 计数原理 章末题型归纳总结(3)云南省昆明市第三中学2023-2024学年高二下学期第二次综合测试(4月)数学试题
4 . 杨辉是我国南宋时期数学家,在其所著的《详解九章算法》一书中,辑录了图①所示的三角形数表,这比欧洲早500多年.杨辉三角本身包含很多性质,并有广泛的应用.借助图②所示的杨辉三角,可以得到,从第0行到第 行:第1斜列之和
行:第1斜列之和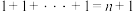 ;第2斜列之和
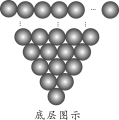
;第2斜列之和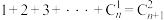 .类比以上结论,并解决如下问题:图③所示为一个
.类比以上结论,并解决如下问题:图③所示为一个 层三角垛,底层是每边堆
层三角垛,底层是每边堆 个圆球的三角形(底层堆积方式如图所示),向上逐层每边少1个,顶层是1个.则小球总数
个圆球的三角形(底层堆积方式如图所示),向上逐层每边少1个,顶层是1个.则小球总数______ .

 行:第1斜列之和
行:第1斜列之和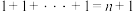 ;第2斜列之和
;第2斜列之和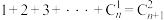 .类比以上结论,并解决如下问题:图③所示为一个
.类比以上结论,并解决如下问题:图③所示为一个 层三角垛,底层是每边堆
层三角垛,底层是每边堆 个圆球的三角形(底层堆积方式如图所示),向上逐层每边少1个,顶层是1个.则小球总数
个圆球的三角形(底层堆积方式如图所示),向上逐层每边少1个,顶层是1个.则小球总数

您最近半年使用:0次
2023-07-09更新
|
277次组卷
|
3卷引用:四川省资阳市2022-2023学年高二下学期期末数学理科试题
5 . 如图,在杨辉三角中,斜线 上方箭头所示的数组成一个锯齿形的数列:
上方箭头所示的数组成一个锯齿形的数列: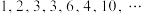 ,记这个数列的前
,记这个数列的前 项和为
项和为 ,则
,则 的值为
的值为__________ .

 上方箭头所示的数组成一个锯齿形的数列:
上方箭头所示的数组成一个锯齿形的数列: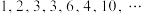 ,记这个数列的前
,记这个数列的前 项和为
项和为 ,则
,则 的值为
的值为
您最近半年使用:0次
6 . 杨辉三角在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中被记载,它的开头几行如图所示,它包含了很多有趣的组合数性质,如果将杨辉三角从第1行开始的每一个数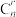 都换成分数
都换成分数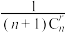 ,得到的三角形称为“莱布尼茨三角形”,莱布尼茨由它得到了很多定理,甚至影响到了微积分的创立,则“莱布尼茨三角形”第8行第5个数是
,得到的三角形称为“莱布尼茨三角形”,莱布尼茨由它得到了很多定理,甚至影响到了微积分的创立,则“莱布尼茨三角形”第8行第5个数是____________ ;若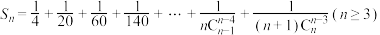 ,则
,则
____________ (用含n的代数式作答).

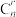 都换成分数
都换成分数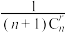 ,得到的三角形称为“莱布尼茨三角形”,莱布尼茨由它得到了很多定理,甚至影响到了微积分的创立,则“莱布尼茨三角形”第8行第5个数是
,得到的三角形称为“莱布尼茨三角形”,莱布尼茨由它得到了很多定理,甚至影响到了微积分的创立,则“莱布尼茨三角形”第8行第5个数是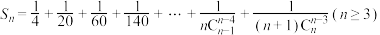 ,则
,则

您最近半年使用:0次
2023-04-18更新
|
413次组卷
|
3卷引用:广东省中山市2022-2023学年高二下学期期末数学试题
7 . “杨辉三角”是中国古代数学文化的瑰宝之一,最早在 年中国南宋数学家杨辉所著的《详解九章算法》一书中出现,欧洲数学家帕斯卡在
年中国南宋数学家杨辉所著的《详解九章算法》一书中出现,欧洲数学家帕斯卡在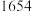 年才发现这一规律,比杨辉要晩近四百年.如图所示的杨辉三角中,从第
年才发现这一规律,比杨辉要晩近四百年.如图所示的杨辉三角中,从第 行开始,每一行除
行开始,每一行除 外,其他每一个数字都是其上一行的左右两个数字之和,若在杨辉三角中存在某一行,满足该行中有三个相邻的数字之比为
外,其他每一个数字都是其上一行的左右两个数字之和,若在杨辉三角中存在某一行,满足该行中有三个相邻的数字之比为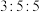 ,则这一行是第
,则这一行是第______ 行.

 年中国南宋数学家杨辉所著的《详解九章算法》一书中出现,欧洲数学家帕斯卡在
年中国南宋数学家杨辉所著的《详解九章算法》一书中出现,欧洲数学家帕斯卡在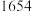 年才发现这一规律,比杨辉要晩近四百年.如图所示的杨辉三角中,从第
年才发现这一规律,比杨辉要晩近四百年.如图所示的杨辉三角中,从第 行开始,每一行除
行开始,每一行除 外,其他每一个数字都是其上一行的左右两个数字之和,若在杨辉三角中存在某一行,满足该行中有三个相邻的数字之比为
外,其他每一个数字都是其上一行的左右两个数字之和,若在杨辉三角中存在某一行,满足该行中有三个相邻的数字之比为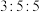 ,则这一行是第
,则这一行是第
您最近半年使用:0次
8 . 杨辉是我国南宋末年的一位杰出的数学家,其著作《详解九章算术》中画了一张表示二项式展开式后的系数构成的三角形数阵(如图所示),称做“开方做法本源”,现简称为“杨辉三角”,比西方的“帕斯卡三角形”早了300多年,若用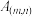 表示三角形数阵中的第m行第n个数,则
表示三角形数阵中的第m行第n个数,则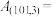
______ (结果用数字作答).
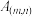 表示三角形数阵中的第m行第n个数,则
表示三角形数阵中的第m行第n个数,则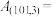

您最近半年使用:0次
2023-01-17更新
|
707次组卷
|
3卷引用:辽宁省沈阳市第二中学2021-2022学年高二上学期期末数学试题
辽宁省沈阳市第二中学2021-2022学年高二上学期期末数学试题重庆市广益中学校2022-2023学年高二下学期4月月考(一)数学试题(已下线)模块四 专题1 高考新题型专练(新定义专练)(人教A)(高二)
9 . 如图所示的杨辉三角中,从第 行开始,每一行除两端的数字是
行开始,每一行除两端的数字是 以外,其他每一个数字都是它肩上两个数字之和在此数阵中,若对于正整数
以外,其他每一个数字都是它肩上两个数字之和在此数阵中,若对于正整数 ,第
,第 行中最大的数为
行中最大的数为 ,第
,第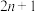 行中最大的数为
行中最大的数为 ,且
,且 ,则
,则 的值为
的值为______ .
 行开始,每一行除两端的数字是
行开始,每一行除两端的数字是 以外,其他每一个数字都是它肩上两个数字之和在此数阵中,若对于正整数
以外,其他每一个数字都是它肩上两个数字之和在此数阵中,若对于正整数 ,第
,第 行中最大的数为
行中最大的数为 ,第
,第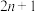 行中最大的数为
行中最大的数为 ,且
,且 ,则
,则 的值为
的值为
您最近半年使用:0次
2022-07-29更新
|
898次组卷
|
7卷引用:安徽省滁州市2021-2022学年高二下学期期末数学试题
安徽省滁州市2021-2022学年高二下学期期末数学试题专题5 综合闯关 (提升版)(已下线)考向38 二项式定理全归纳(十五大经典题型)-3(已下线)第三章 排列、组合与二项式定理(A卷·知识通关练)(3)(已下线)3.3二项式定理与杨辉三角(3)(已下线)第5讲 二项式定理11种题型总结(4)(已下线)考点06 杨辉三角 2024届高考数学考点总动员【讲】
10 . “杨辉三角”是中国数学史上的一个伟大成就,激发起一批又一批数学爱好者的探究欲望.它揭示了二项式系数在三角形中的一种几何排列规律,早在南宋时期数学家杨辉1261年所著的《详解九章算法》一书中出现这一规律,而欧洲数学家帕斯卡在1654年才发现这一规律,比杨辉要晚近四百年.如图,在由二项式系数所构成的“杨辉三角”中,第11行中从左至右第5与第6个数的比值为_________ .


您最近半年使用:0次



