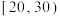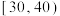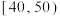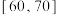名校
1 . 下列命题中正确的是( )
A.数据 的第25百分位数是2 的第25百分位数是2 |
B.若事件 的概率满足 的概率满足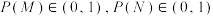 且 且 ,则 ,则 相互独立 相互独立 |
C.已知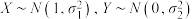 ,则 ,则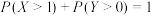 |
D.已知随机变量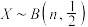 ,若 ,若 ,则 ,则 |
您最近半年使用:0次
2023-09-01更新
|
228次组卷
|
3卷引用:贵州省三新改革联盟校2022-2023学年7月高二下学期期末联考数学试题
2 . 为了研究学生每天整理数学错题情况,将一周有4天及以上整理数学错题视为“经常整理”,少于4天视为“不经常整理”,某课题组在某市中学生中随机抽取了100人调查,其中数学成绩优秀的40人,数学成绩不优秀的60人,调查结果显示,数学成绩优秀的有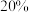 表示自己不经常整理,数学成绩不优秀的有32人不经常整理,为了分析数学成绩优秀与是否经常整理数学错题有关,构建了
表示自己不经常整理,数学成绩不优秀的有32人不经常整理,为了分析数学成绩优秀与是否经常整理数学错题有关,构建了 列联表:
列联表:
(1)请将 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有 的把握认为经常整理数学错题与数学成绩优秀有关;
的把握认为经常整理数学错题与数学成绩优秀有关;
(2)从数学成绩优秀学生中是否经常整理数学错题为标准采取分层抽样方式抽出10人,再从这10人中随机抽出2人,若所选2人中不经常整理数学错题人数为 ,求
,求 分布列及期望.
分布列及期望.
附: .
.
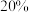 表示自己不经常整理,数学成绩不优秀的有32人不经常整理,为了分析数学成绩优秀与是否经常整理数学错题有关,构建了
表示自己不经常整理,数学成绩不优秀的有32人不经常整理,为了分析数学成绩优秀与是否经常整理数学错题有关,构建了 列联表:
列联表:| 不经常整理数学错题 | 经常整理数学错题 | 总计 | |
| 数学成绩优秀 | |||
| 数学成绩不优秀 | |||
| 总计 |
 列联表补充完整,并判断能否有
列联表补充完整,并判断能否有 的把握认为经常整理数学错题与数学成绩优秀有关;
的把握认为经常整理数学错题与数学成绩优秀有关;(2)从数学成绩优秀学生中是否经常整理数学错题为标准采取分层抽样方式抽出10人,再从这10人中随机抽出2人,若所选2人中不经常整理数学错题人数为
 ,求
,求 分布列及期望.
分布列及期望.附:
 .
.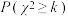 |  | 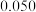 |  |  |  |
 |  |  |  |  |  |
您最近半年使用:0次
解题方法
3 . 一名射击运动员射击一次击中目标的概率为 ,各次射击互不影响.若他连续射击两次,则下列说法正确的是( )
,各次射击互不影响.若他连续射击两次,则下列说法正确的是( )
 ,各次射击互不影响.若他连续射击两次,则下列说法正确的是( )
,各次射击互不影响.若他连续射击两次,则下列说法正确的是( )| A.事件“至多击中一次”与“恰击中一次”互斥 |
| B.事件“两次均未击中”与“至少击中一次”相互对立 |
| C.事件“第一次击中”与“两次均击中”相互独立 |
D.记 为击中目标的次数,则 为击中目标的次数,则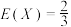 , ,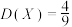 |
您最近半年使用:0次
名校
4 . 新型冠状病毒是一种急性的传染性疾病,传播速度很快,它的传播途径主要是飞沫传播、口液传播以及接触传播等,传播速度最快的是飞沫传播.佩戴口罩能有效预防新冠病毒的感染,双方都戴口罩的情况下新冠病毒感染的几率大概只有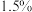 ,如果戴口罩再加上保持1.8米的距离,感染的几率是
,如果戴口罩再加上保持1.8米的距离,感染的几率是 ,如果双方都不戴口罩,那么感染几率高达
,如果双方都不戴口罩,那么感染几率高达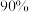 .为了调查不同年龄层的人对“佩戴口罩”的态度,研究人员随机抽取了300人,并将所得结果统计如下表所示.
.为了调查不同年龄层的人对“佩戴口罩”的态度,研究人员随机抽取了300人,并将所得结果统计如下表所示.
(1)完成下列 列联表,并判断是否有
列联表,并判断是否有 的把握认为年龄与戴口罩态度具有相关性;
的把握认为年龄与戴口罩态度具有相关性;
(2)现从年龄在50周岁以上(含50周岁)的样本中按是否愿意佩戴口罩,用分层抽样法抽取6人,再从这6人中随机抽取3人,记抽出的3人中不愿戴口罩的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
参考公式: .
.
参考数据:
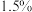 ,如果戴口罩再加上保持1.8米的距离,感染的几率是
,如果戴口罩再加上保持1.8米的距离,感染的几率是 ,如果双方都不戴口罩,那么感染几率高达
,如果双方都不戴口罩,那么感染几率高达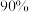 .为了调查不同年龄层的人对“佩戴口罩”的态度,研究人员随机抽取了300人,并将所得结果统计如下表所示.
.为了调查不同年龄层的人对“佩戴口罩”的态度,研究人员随机抽取了300人,并将所得结果统计如下表所示.年龄 |
|
|
|
|
|
频数 | 30 | 75 | 105 | 60 | 30 |
愿意戴口罩 | 24 | 66 | 90 | 42 | 18 |
 列联表,并判断是否有
列联表,并判断是否有 的把握认为年龄与戴口罩态度具有相关性;
的把握认为年龄与戴口罩态度具有相关性;年龄在50周岁以上(含50周岁) | 年龄在50周岁以下 | 合计 | |
愿意戴口罩 | |||
不愿意戴口罩 | |||
合计 |
 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.参考公式:
 .
.参考数据:
 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
解题方法
5 . 下列说法正确的有( )
A.若变量 关于 关于 的经验回归方程为 的经验回归方程为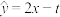 且 且 , , ,则 ,则 |
B.若随机变量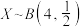 ,则 ,则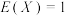 |
C.在回归模型中,决定系数 越大,模型的拟合效果越好 越大,模型的拟合效果越好 |
D.若随机变量的方差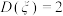 ,则 ,则 |
您最近半年使用:0次
6 . 2022年2月4日—2月20日北京冬奥会如期举行,各国媒体争相报道运动会盛况,因此每天有很多民众通过手机、电视等方式观看冬奥新闻.某机构将每天关注冬奥时间在1小时以上的人称为“冬奥迷”,否则称为“非冬奥迷”,通过调查并从参与调查的人群中随机抽取了200人进行抽样分析,得到下表(单位:人):
(1)根据以上数据,能否在犯错误的概率不超过0.01的前提下认为“非冬奥迷”还是“冬奥迷”与年龄有关?
(2)现从抽取的50岁及以下的人中,按“非冬奥迷”与“冬奥迷”这两种类型进行分层抽样抽取5人,然后,将从这5人中随机选出2人,其中“冬奥迷”的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
参考公式: ,其中
,其中 .
.
参考数据:
非冬奥迷 | 冬奥迷 | 合计 | |
50岁及以下 | 40 | 60 | 100 |
50岁以上 | 80 | 20 | 100 |
合计 | 120 | 80 | 200 |
(2)现从抽取的50岁及以下的人中,按“非冬奥迷”与“冬奥迷”这两种类型进行分层抽样抽取5人,然后,将从这5人中随机选出2人,其中“冬奥迷”的人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.参考公式:
 ,其中
,其中 .
.参考数据:
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
解题方法
7 . 甲、乙两人下象棋比赛,规则如下:由抽签确定第1局先下棋的人选,第1局先下棋的人是甲、乙的概率各为0.5,赢得本局的人下一局先下棋.若甲先下棋,则甲本局获胜的概率为0.6,若乙先下棋,则甲本局获胜的概率为0.5,每局比赛无平局且每局比赛的胜负结果相互独立
(1)求第2局甲先下棋的概率;
(2)若比赛采用5局3胜制,且第一局甲先下棋,记 为比赛结束时进行的局数,求
为比赛结束时进行的局数,求 的分布列和数学期望.
的分布列和数学期望.
(1)求第2局甲先下棋的概率;
(2)若比赛采用5局3胜制,且第一局甲先下棋,记
 为比赛结束时进行的局数,求
为比赛结束时进行的局数,求 的分布列和数学期望.
的分布列和数学期望.
您最近半年使用:0次
8 . 来自微碧江的报道:2023年6月17日,铜仁市碧江区第二届房地产交易展示会在三江公园隆重开幕.据了解,本次房交会以政府搭台、企业让利、政策支持、百姓受益为办展宗旨,聚集了碧江区17家房开企业、18个楼盘参展,2080套房源、25万平方米供群众选购,9大银行和公积金中心在现场助阵和提供咨询服务.本次房交会从6月17日持续到6月22日,期间每天都安排有精彩演出、免费美食、互动游戏、露天电影和游江龙舟五类活动.
(1)甲、乙两名市民参加了不同类的活动,且每人只参加一类活动.已知甲参加了免费美食的活动,求乙参加游江龙舟活动的概率是多少?
(2)已知来自某小区的市民参加互动游戏的概率是 ,设来自该小区的2名市民参加互动游戏的人数为
,设来自该小区的2名市民参加互动游戏的人数为 ,求
,求 的分布列与期望.
的分布列与期望.
(1)甲、乙两名市民参加了不同类的活动,且每人只参加一类活动.已知甲参加了免费美食的活动,求乙参加游江龙舟活动的概率是多少?
(2)已知来自某小区的市民参加互动游戏的概率是
 ,设来自该小区的2名市民参加互动游戏的人数为
,设来自该小区的2名市民参加互动游戏的人数为 ,求
,求 的分布列与期望.
的分布列与期望.
您最近半年使用:0次
解题方法
9 . 猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名.某嘉宾参加猜歌名节目,猜对每首歌曲的歌名相互独立,猜对三首歌曲 歌名的概率及猜对时获得相应的公益基金如下表所示.
歌名的概率及猜对时获得相应的公益基金如下表所示.
(1)该嘉宾从 三首歌曲中随机选择一首,求该嘉宾猜对歌名的概率.
三首歌曲中随机选择一首,求该嘉宾猜对歌名的概率.
(2)若猜歌名的规则如下:按照 的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额
的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额 的分布列及均值.
的分布列及均值.
 歌名的概率及猜对时获得相应的公益基金如下表所示.
歌名的概率及猜对时获得相应的公益基金如下表所示.| 歌曲 |  |  |  |
| 猜对的概率 | 0.6 | 0.5 | 0.3 |
| 获得的公益基金额/元 | 1000 | 2000 | 3000 |
 三首歌曲中随机选择一首,求该嘉宾猜对歌名的概率.
三首歌曲中随机选择一首,求该嘉宾猜对歌名的概率.(2)若猜歌名的规则如下:按照
 的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额
的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额 的分布列及均值.
的分布列及均值.
您最近半年使用:0次
10 . 2022年9月23日,延期后的杭州亚运会迎来倒计时一周年,杭州亚组委发布宣传片《亚运+1》和主办城市推广曲《最美的风景》.杭州某大学从全校学生中随机抽取了1200名学生,对是否收看宣传片的情况进行了问卷调查,统计数据如下,
(1)根据以上数据说明,依据小概率值 的独立性检验,能否认为学生是否收看宣传片与性别有关?
的独立性检验,能否认为学生是否收看宣传片与性别有关?
(2)现从参与问卷调查且收看了宣传片的学生中,按性别采用分层抽样的方法选取8人,参加杭州2023年第19届亚运会志愿者宣传活动.若从这8人中随机选取2人到校广播站开展亚运会比赛项目宣传介绍.记 为人选的2人中女生的人数,求随机变量
为人选的2人中女生的人数,求随机变量 的分布列及数学期望.
的分布列及数学期望.
参考公式和数据: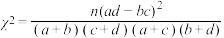 ,
, .
.
收看 | 未收看 | |
男生 | 600 | 200 |
女生 | 200 | 200 |
 的独立性检验,能否认为学生是否收看宣传片与性别有关?
的独立性检验,能否认为学生是否收看宣传片与性别有关?(2)现从参与问卷调查且收看了宣传片的学生中,按性别采用分层抽样的方法选取8人,参加杭州2023年第19届亚运会志愿者宣传活动.若从这8人中随机选取2人到校广播站开展亚运会比赛项目宣传介绍.记
 为人选的2人中女生的人数,求随机变量
为人选的2人中女生的人数,求随机变量 的分布列及数学期望.
的分布列及数学期望.参考公式和数据:
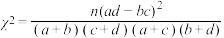 ,
, .
.
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
2023-05-03更新
|
448次组卷
|
2卷引用:贵州省黔西南州2022-2023学年高二下学期期末教学质量检测数学试题