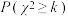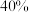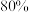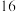名校
解题方法
1 . 清明小长假期间,大连市共接待客流322.11万人次,游客接待量与收入达到同期历史峰值,其中到东港旅游的人数达到百万之多.现对到东港旅游的部分游客做问卷调查,其中 的人只游览东方水城,另外
的人只游览东方水城,另外 的人游览东方水城和港东五街.若某位游客只游览东方水城,记1分,若两项都游览,记2分.视频率为概率,解答下列问题.
的人游览东方水城和港东五街.若某位游客只游览东方水城,记1分,若两项都游览,记2分.视频率为概率,解答下列问题.
(1)从到东港旅游的游客中随机抽取3人,记这3人的合计得分为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)从到东港旅游的游客中随机抽取 人
人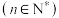 ,记这
,记这 人的合计得分恰为
人的合计得分恰为 分的概率为
分的概率为 ,求
,求 ;
;
(3)从到东港旅游的游客中随机抽取10人,其中两处景点都去的人数为 .记两处景点都去的人数为
.记两处景点都去的人数为 的概率为
的概率为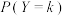 ,写出
,写出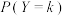 的表达式,并求出当
的表达式,并求出当 为何值时,
为何值时,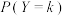 最大?
最大?
 的人只游览东方水城,另外
的人只游览东方水城,另外 的人游览东方水城和港东五街.若某位游客只游览东方水城,记1分,若两项都游览,记2分.视频率为概率,解答下列问题.
的人游览东方水城和港东五街.若某位游客只游览东方水城,记1分,若两项都游览,记2分.视频率为概率,解答下列问题.(1)从到东港旅游的游客中随机抽取3人,记这3人的合计得分为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)从到东港旅游的游客中随机抽取
 人
人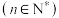 ,记这
,记这 人的合计得分恰为
人的合计得分恰为 分的概率为
分的概率为 ,求
,求 ;
;(3)从到东港旅游的游客中随机抽取10人,其中两处景点都去的人数为
 .记两处景点都去的人数为
.记两处景点都去的人数为 的概率为
的概率为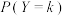 ,写出
,写出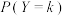 的表达式,并求出当
的表达式,并求出当 为何值时,
为何值时,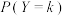 最大?
最大?
您最近一年使用:0次
名校
2 . 乒乓球,被称为中国的“国球”.某中学对学生参加乒乓球运动的情况进行调查,将每周参加乒乓球运动超过2小时的学生称为“乒乓球爱好者”,否则称为“非乒乓球爱好者”,从调查结果中随机抽取100份进行分析,得到数据如表所示:
(1)补全 列联表,并判断我们能否有
列联表,并判断我们能否有 的把握认为是否为“乒乓球爱好者”与性别有关?
的把握认为是否为“乒乓球爱好者”与性别有关?
(2)为了解学生的乒乓球运动水平,现从抽取的“乒乓球爱好者”学生中按性别采用分层抽样的方法抽取3人,与体育老师进行乒乓球比赛,其中男乒乓球爱好者获胜的概率为 ,女乒乓球爱好者获胜的概率为
,女乒乓球爱好者获胜的概率为 ,每次比赛结果相互独立,记这3人获胜的人数为
,每次比赛结果相互独立,记这3人获胜的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式: .
.
乒乓球爱好者 | 非乒乓球爱好者 | 总计 | |
男 | 40 | 56 | |
女 | 24 | ||
总计 | 100 |
 列联表,并判断我们能否有
列联表,并判断我们能否有 的把握认为是否为“乒乓球爱好者”与性别有关?
的把握认为是否为“乒乓球爱好者”与性别有关?(2)为了解学生的乒乓球运动水平,现从抽取的“乒乓球爱好者”学生中按性别采用分层抽样的方法抽取3人,与体育老师进行乒乓球比赛,其中男乒乓球爱好者获胜的概率为
 ,女乒乓球爱好者获胜的概率为
,女乒乓球爱好者获胜的概率为 ,每次比赛结果相互独立,记这3人获胜的人数为
,每次比赛结果相互独立,记这3人获胜的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
| 0.05 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
 .
.
您最近一年使用:0次
2024-04-10更新
|
1055次组卷
|
6卷引用:辽宁省大连市第八中学2023-2024学年高二下学期期中考试数学试题
辽宁省大连市第八中学2023-2024学年高二下学期期中考试数学试题四川省绵阳市三台中学校2024届高三下学期第三学月(4月)月考理科数学试题(已下线)8.3.1分类变量与列联表+8.3.2独立性检验 第三练 能力提升拔高四川省成都市石室阳安学校2023-2024学年高三下学期4月月考数学(理)试题(已下线)第八章 成对数据的统计分析总结 第一课归纳本章考点2024届陕西省富平县高三第二次模拟理科数学试题
名校
3 . 某微信群群主为了了解微信随机红包的金额拆分机制,统计了本群最近一周内随机红包(假设每个红包的总金额均相等)的金额数据(单位:元),绘制了如下频率分布直方图.

(1)根据频率分布直方图估计红包金额的平均值与众数;
(2)群主预告今天晚上7点将有3个随机红包,每个红包的总金额均相等且每个人都能抢到红包.小明是该群的一位成员,以频率作为概率,求小明至少两次抢到10元以上金额的红包的概率.
(3)在春节期间,群主为了活跃气氛,在群内发起抢红包游戏规定:每轮“手气最佳”者发下一轮红包,每个红包发出后,所有人都参与抢红包.第一个红包由群主发.根据以往抢红包经验,群主自己发红包时,抢到“手气最佳”的概率为 ;其他成员发红包时,群主抢到“手气最佳”的概率为
;其他成员发红包时,群主抢到“手气最佳”的概率为 .设前
.设前 轮中群主发红包的次数为
轮中群主发红包的次数为 ,第
,第 轮由群主发红包的概率为
轮由群主发红包的概率为 .求
.求 及
及 的期望
的期望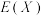 .
.

(1)根据频率分布直方图估计红包金额的平均值与众数;
(2)群主预告今天晚上7点将有3个随机红包,每个红包的总金额均相等且每个人都能抢到红包.小明是该群的一位成员,以频率作为概率,求小明至少两次抢到10元以上金额的红包的概率.
(3)在春节期间,群主为了活跃气氛,在群内发起抢红包游戏规定:每轮“手气最佳”者发下一轮红包,每个红包发出后,所有人都参与抢红包.第一个红包由群主发.根据以往抢红包经验,群主自己发红包时,抢到“手气最佳”的概率为
 ;其他成员发红包时,群主抢到“手气最佳”的概率为
;其他成员发红包时,群主抢到“手气最佳”的概率为 .设前
.设前 轮中群主发红包的次数为
轮中群主发红包的次数为 ,第
,第 轮由群主发红包的概率为
轮由群主发红包的概率为 .求
.求 及
及 的期望
的期望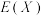 .
.
您最近一年使用:0次
2024-03-23更新
|
2042次组卷
|
5卷引用:辽宁省大连市第八中学2023-2024学年高二下学期期中考试数学试题
辽宁省大连市第八中学2023-2024学年高二下学期期中考试数学试题重庆市南开中学校2023-2024学年高三下学期第七次质量检测数学试题(已下线)数学(上海卷02)(已下线)数学(上海卷01)(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点1 随机变量的分布列、期望(二)【培优版】
4 . 在某游戏中,小明遇到了如图的开关阵列,每个开关只有开和关两个状态,摁下某个开关会导致自身及相邻位置的开关状态发生变化.例如摁下 会导致
会导致
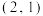

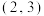
 发生状态变化.开始时所有开关均关闭.
发生状态变化.开始时所有开关均关闭.
(1)如果随机摁下一个开关,求最终状态为“打开”的的开关数目为4的概率.
(2)如果从上两排六个开关中随机选择并摁下两个不同的开关,求摁下第一排和第二排各一个开关的概率.
(3)如果依次按下两个开关,求最终状态为“打开”的开关数目为4的概率.
 会导致
会导致
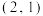

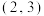
 发生状态变化.开始时所有开关均关闭.
发生状态变化.开始时所有开关均关闭. |  | 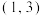 |
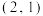 |  | 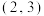 |
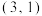 |  |  |
(2)如果从上两排六个开关中随机选择并摁下两个不同的开关,求摁下第一排和第二排各一个开关的概率.
(3)如果依次按下两个开关,求最终状态为“打开”的开关数目为4的概率.
您最近一年使用:0次
名校
5 . 人工智能 是一门极富挑战性的科学,自诞生以来,理论和技术日益成熟.某校成立了
是一门极富挑战性的科学,自诞生以来,理论和技术日益成熟.某校成立了 、
、 两个研究性小组,分别设计和开发不同的
两个研究性小组,分别设计和开发不同的 软件用于识别音乐的类别:“古典音乐”、“流行音乐”和“民族音乐”.为测试
软件用于识别音乐的类别:“古典音乐”、“流行音乐”和“民族音乐”.为测试 软件的识别能力,计划采取两种测试方案.
软件的识别能力,计划采取两种测试方案.
方案一:将 首音乐随机分配给
首音乐随机分配给 、
、 两个小组识别.每首音乐只被一个
两个小组识别.每首音乐只被一个 软件识别一次,并记录结果;
软件识别一次,并记录结果;
方案二:对同一首音乐, 、
、 两组分别识别两次,如果识别的正确次数之和不少于三次,则称该次测试通过.
两组分别识别两次,如果识别的正确次数之和不少于三次,则称该次测试通过.
(1)若方案一的测试结果显示:正确识别的音乐数之和占总数的 ;在正确识别的音乐数中,
;在正确识别的音乐数中, 组占
组占 ;在错误识别的音乐数中,
;在错误识别的音乐数中, 组占
组占 .
.
(i)用频率估计概率,两个研究性小组的 软件每次能正确识别音乐类别的概率分别为多少?
软件每次能正确识别音乐类别的概率分别为多少?
(ii)利用(i)中的结论,求方案二在一次测试中获得通过的概率:
(2)若方案一的测试结果如下:
在 小组、
小组、 小组识别的歌曲中各任选
小组识别的歌曲中各任选 首,记
首,记 、
、 分别为
分别为 小组、
小组、 小组正确识别的数量,试比较
小组正确识别的数量,试比较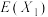 、
、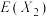 的大小(直接写出结果即可).
的大小(直接写出结果即可).
 是一门极富挑战性的科学,自诞生以来,理论和技术日益成熟.某校成立了
是一门极富挑战性的科学,自诞生以来,理论和技术日益成熟.某校成立了 、
、 两个研究性小组,分别设计和开发不同的
两个研究性小组,分别设计和开发不同的 软件用于识别音乐的类别:“古典音乐”、“流行音乐”和“民族音乐”.为测试
软件用于识别音乐的类别:“古典音乐”、“流行音乐”和“民族音乐”.为测试 软件的识别能力,计划采取两种测试方案.
软件的识别能力,计划采取两种测试方案.方案一:将
 首音乐随机分配给
首音乐随机分配给 、
、 两个小组识别.每首音乐只被一个
两个小组识别.每首音乐只被一个 软件识别一次,并记录结果;
软件识别一次,并记录结果;方案二:对同一首音乐,
 、
、 两组分别识别两次,如果识别的正确次数之和不少于三次,则称该次测试通过.
两组分别识别两次,如果识别的正确次数之和不少于三次,则称该次测试通过.(1)若方案一的测试结果显示:正确识别的音乐数之和占总数的
 ;在正确识别的音乐数中,
;在正确识别的音乐数中, 组占
组占 ;在错误识别的音乐数中,
;在错误识别的音乐数中, 组占
组占 .
.(i)用频率估计概率,两个研究性小组的
 软件每次能正确识别音乐类别的概率分别为多少?
软件每次能正确识别音乐类别的概率分别为多少?(ii)利用(i)中的结论,求方案二在一次测试中获得通过的概率:
(2)若方案一的测试结果如下:
音乐类别 |
|
| ||
测试音乐数量 | 正确识别比例 | 测试音乐数量 | 正确识别比例 | |
古典音乐 |
|
|
|
|
流行音乐 |
|
|
|
|
民族音乐 |
|
|
|
|
 小组、
小组、 小组识别的歌曲中各任选
小组识别的歌曲中各任选 首,记
首,记 、
、 分别为
分别为 小组、
小组、 小组正确识别的数量,试比较
小组正确识别的数量,试比较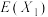 、
、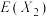 的大小(直接写出结果即可).
的大小(直接写出结果即可).
您最近一年使用:0次
2023-05-28更新
|
584次组卷
|
3卷引用:辽宁省大连市第八中学2022-2023学年高二下学期6月月考数学试题
名校
解题方法
6 . 为纪念中国共产党成立102周年,加深青少年对党的历史、党的知识、党的理论和路线方针的认识,激发爱党爱国热情,坚定走新时代中国特色社会主义道路的信心,我校举办了党史知识竞赛.竞赛规则是:两人一组,每一轮竞赛中,小组两人分别答3道题,若答对题目不少于5道题,则获得一个积分.已知甲乙两名同学一组,甲同学和乙同学对每道题答对的概率分别是 和
和 ,且每道题答对与否互不影响.
,且每道题答对与否互不影响.
(1)若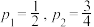 ,求甲乙同学这一组在一轮竞赛中获得一个积分的概率;
,求甲乙同学这一组在一轮竞赛中获得一个积分的概率;
(2)若 ,且每轮比赛互不影响,若甲乙同学这一组想至少获得7个积分,那么理论上至少要进行多少轮竞赛?
,且每轮比赛互不影响,若甲乙同学这一组想至少获得7个积分,那么理论上至少要进行多少轮竞赛?
 和
和 ,且每道题答对与否互不影响.
,且每道题答对与否互不影响.(1)若
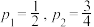 ,求甲乙同学这一组在一轮竞赛中获得一个积分的概率;
,求甲乙同学这一组在一轮竞赛中获得一个积分的概率;(2)若
 ,且每轮比赛互不影响,若甲乙同学这一组想至少获得7个积分,那么理论上至少要进行多少轮竞赛?
,且每轮比赛互不影响,若甲乙同学这一组想至少获得7个积分,那么理论上至少要进行多少轮竞赛?
您最近一年使用:0次
2023-05-24更新
|
985次组卷
|
3卷引用:辽宁省大连市第二十四中学2023届高三第六次模拟考试数学试卷
名校
解题方法
7 . 国学小组有编号为1,2,3,…, 的
的 位同学,现在有两个选择题,每人答对第一题的概率为
位同学,现在有两个选择题,每人答对第一题的概率为 、答对第二题的概率为
、答对第二题的概率为 ,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第
,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第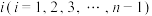 号同学未答对第一题,则第
号同学未答对第一题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继继续比赛;③若第
号同学继继续比赛;③若第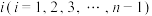 号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第
号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第 轮结束;若该生未答对第二题,则第
轮结束;若该生未答对第二题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第
号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第 轮,则不管第
轮,则不管第 号同学答题情况,比赛结束.
号同学答题情况,比赛结束.
(1)令随机变量 表示
表示 名同学在第
名同学在第 轮比赛结束,当
轮比赛结束,当 时,求随机变量
时,求随机变量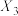 的分布列;
的分布列;
(2)若把比赛规则③改为:若第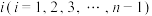 号同学未答对第二题,则第
号同学未答对第二题,则第 轮比赛失败,第
轮比赛失败,第 号同学重新从第一题开始作答.令随机变量
号同学重新从第一题开始作答.令随机变量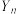 表示
表示 名挑战者在第
名挑战者在第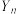 轮比赛结束.
轮比赛结束.
①求随机变量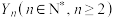 的分布列;
的分布列;
②证明: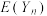 单调递增,且小于3.
单调递增,且小于3.
 的
的 位同学,现在有两个选择题,每人答对第一题的概率为
位同学,现在有两个选择题,每人答对第一题的概率为 、答对第二题的概率为
、答对第二题的概率为 ,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第
,每个同学的答题过程都是相互独立的,比赛规则如下:①按编号由小到大的顺序依次进行,第1号同学开始第1轮出赛,先答第一题;②若第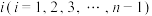 号同学未答对第一题,则第
号同学未答对第一题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继继续比赛;③若第
号同学继继续比赛;③若第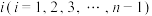 号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第
号同学答对第一题,则再答第二题,若该生答对第二题,则比赛在第 轮结束;若该生未答对第二题,则第
轮结束;若该生未答对第二题,则第 轮比赛失败,由第
轮比赛失败,由第 号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第
号同学继续答第二题,且以后比赛的同学不答第一题;④若比赛进行到了第 轮,则不管第
轮,则不管第 号同学答题情况,比赛结束.
号同学答题情况,比赛结束.(1)令随机变量
 表示
表示 名同学在第
名同学在第 轮比赛结束,当
轮比赛结束,当 时,求随机变量
时,求随机变量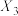 的分布列;
的分布列;(2)若把比赛规则③改为:若第
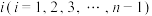 号同学未答对第二题,则第
号同学未答对第二题,则第 轮比赛失败,第
轮比赛失败,第 号同学重新从第一题开始作答.令随机变量
号同学重新从第一题开始作答.令随机变量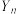 表示
表示 名挑战者在第
名挑战者在第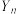 轮比赛结束.
轮比赛结束.①求随机变量
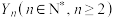 的分布列;
的分布列;②证明:
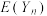 单调递增,且小于3.
单调递增,且小于3.
您最近一年使用:0次
2023-04-13更新
|
4623次组卷
|
9卷引用:辽宁省大连市2023届高三一模数学试题
辽宁省大连市2023届高三一模数学试题东北三省四市教研联合体2023届高三一模数学试题吉林省长春市2023届高三三模数学试题(已下线)模块四 专题5 概率与统计(已下线)押新高考第19题 概率统计安徽省滁州市定远县育才学校2023届高考冲刺数学试卷(三)江苏省苏州工业园区星海实验中学2022-2023学年高二下学期5月阶段检测数学试题云南省曲靖市第二中学2023届高三二模预测数学试题(已下线)专题8-2分布列综合归类-2
名校
8 . 党的二十大报告中指出,建设现代化产业体系,坚持把发展经济的着力点放在实体经济上,推进新型工业化,加快建设制造强国、质量强国、航天强国、交通强国、网络强国、数字中国.某装备制造企业对现有生产设备进行技术攻坚突破.设备生产的零件的直径为X(单位nm).
(1)现有旧设备生产的零件共7个,其中直径大于10nm的有4个.现从这7个零件中随机抽取3个.记 表示取出的零件中直径大于10nm的零件的个数,求
表示取出的零件中直径大于10nm的零件的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)技术攻坚突破后设备生产的零件的合格率为 ,每个零件是否合格相互独立.现任取6个零件进行检测,若合格的零件数
,每个零件是否合格相互独立.现任取6个零件进行检测,若合格的零件数 超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及
超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及 的方差;
的方差;
(3)若技术攻坚后新设备生产的零件直径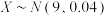 ,从生产的零件中随机取出10个,求至少有一个零件直径大于9.03nm的概率.
,从生产的零件中随机取出10个,求至少有一个零件直径大于9.03nm的概率.
参考数据: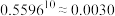 ,
,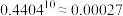 ,标准正态分布函数表如下:
,标准正态分布函数表如下:
(1)现有旧设备生产的零件共7个,其中直径大于10nm的有4个.现从这7个零件中随机抽取3个.记
 表示取出的零件中直径大于10nm的零件的个数,求
表示取出的零件中直径大于10nm的零件的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;(2)技术攻坚突破后设备生产的零件的合格率为
 ,每个零件是否合格相互独立.现任取6个零件进行检测,若合格的零件数
,每个零件是否合格相互独立.现任取6个零件进行检测,若合格的零件数 超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及
超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及 的方差;
的方差;(3)若技术攻坚后新设备生产的零件直径
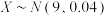 ,从生产的零件中随机取出10个,求至少有一个零件直径大于9.03nm的概率.
,从生产的零件中随机取出10个,求至少有一个零件直径大于9.03nm的概率.参考数据:
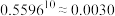 ,
,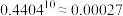 ,标准正态分布函数表如下:
,标准正态分布函数表如下:
a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
0.0 | .5000 | .5040 | .5080 | .5120 | .5160 | .5199 | .5239 | .5279 | .5319 | .5359 |
0.1 | .5398 | .5438 | .5478 | .5517 | .5557 | .5596 | .5636 | .5675 | .5714 | .5753 |
0.2 | .5793 | .5832 | .5871 | .5910 | .5948 | .5987 | .6026 | .6064 | .6103 | .6141 |
0.3 | .6179 | .6217 | .6255 | .6293 | .6331 | .6368 | .6406 | .6443 | .6480 | .6517 |
0.4 | .6554 | .6591 | .6628 | .6664 | .6700 | .6736 | .6772 | .6808 | .6844 | .6879 |
0.5 | .6915 | .6950 | .6985 | .7019 | .7054 | .7088 | .7123 | .7157 | .7190 | .7224 |
您最近一年使用:0次
解题方法
9 . 某地区为居民集体筛查新型传染病毒,需要核酸检测,现有 份样本,有以下两种检验方案,方案一,逐份检验,则需要检验k次;方案二:混合检验,将k份样本分别取样混合在一起检验一次,若检验结果为阴性,则k份样本均为阴性,若检验结果为阳性,为了确定k份样本的阳性样本,则对k份本再逐一检验.逐份检验和混合检验中的每一次检验费用都是16元,且k份样本混合检验一次需要额外收20元的材料费和服务费.假设在接受检验的样本中,每份样本是否为阳性是相互独立的,且据统计每份样本是阴性的概率为
份样本,有以下两种检验方案,方案一,逐份检验,则需要检验k次;方案二:混合检验,将k份样本分别取样混合在一起检验一次,若检验结果为阴性,则k份样本均为阴性,若检验结果为阳性,为了确定k份样本的阳性样本,则对k份本再逐一检验.逐份检验和混合检验中的每一次检验费用都是16元,且k份样本混合检验一次需要额外收20元的材料费和服务费.假设在接受检验的样本中,每份样本是否为阳性是相互独立的,且据统计每份样本是阴性的概率为 .
.
(1)若 份样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;
份样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;
(2)①若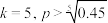 ,以检验总费用为决策依据,试说明该单位选择方案二的合理性;
,以检验总费用为决策依据,试说明该单位选择方案二的合理性;
②若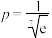 ,采用方案二总费用的数学期望低于方案一,求k的最大值.
,采用方案二总费用的数学期望低于方案一,求k的最大值.
参考数据: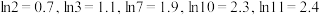
 份样本,有以下两种检验方案,方案一,逐份检验,则需要检验k次;方案二:混合检验,将k份样本分别取样混合在一起检验一次,若检验结果为阴性,则k份样本均为阴性,若检验结果为阳性,为了确定k份样本的阳性样本,则对k份本再逐一检验.逐份检验和混合检验中的每一次检验费用都是16元,且k份样本混合检验一次需要额外收20元的材料费和服务费.假设在接受检验的样本中,每份样本是否为阳性是相互独立的,且据统计每份样本是阴性的概率为
份样本,有以下两种检验方案,方案一,逐份检验,则需要检验k次;方案二:混合检验,将k份样本分别取样混合在一起检验一次,若检验结果为阴性,则k份样本均为阴性,若检验结果为阳性,为了确定k份样本的阳性样本,则对k份本再逐一检验.逐份检验和混合检验中的每一次检验费用都是16元,且k份样本混合检验一次需要额外收20元的材料费和服务费.假设在接受检验的样本中,每份样本是否为阳性是相互独立的,且据统计每份样本是阴性的概率为 .
.(1)若
 份样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;
份样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;(2)①若
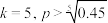 ,以检验总费用为决策依据,试说明该单位选择方案二的合理性;
,以检验总费用为决策依据,试说明该单位选择方案二的合理性;②若
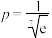 ,采用方案二总费用的数学期望低于方案一,求k的最大值.
,采用方案二总费用的数学期望低于方案一,求k的最大值.参考数据:
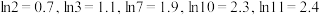
您最近一年使用:0次
2022-12-30更新
|
559次组卷
|
2卷引用:辽宁省大连市2023届高三上学期期末双基测试数学试题
10 . 甲、乙是北京2022冬奥会单板滑雪坡面障碍技巧项目的参赛选手,二人在练习赛中均需要挑战3次某高难度动作,每次挑战的结果只有成功和失败两种.
(1)甲在每次挑战中,成功的概率都为 .设X为甲在3次挑战中成功的次数,求X的分布列和数学期望;
.设X为甲在3次挑战中成功的次数,求X的分布列和数学期望;
(2)乙在第一次挑战时,成功的概率为0.5,受心理因素影响,从第二次开始,每次成功的概率会发生改变其规律为:若前一次成功,则该次成功的概率比前一次成功的概率增加0.1;若前一次失败,则该次成功的概率比前一次成功的概率减少0.1.
(ⅰ)求乙在前两次挑战中,恰好成功一次的概率;
(ⅱ)求乙在第二次成功的条件下,第三次成功的概率.
(1)甲在每次挑战中,成功的概率都为
 .设X为甲在3次挑战中成功的次数,求X的分布列和数学期望;
.设X为甲在3次挑战中成功的次数,求X的分布列和数学期望;(2)乙在第一次挑战时,成功的概率为0.5,受心理因素影响,从第二次开始,每次成功的概率会发生改变其规律为:若前一次成功,则该次成功的概率比前一次成功的概率增加0.1;若前一次失败,则该次成功的概率比前一次成功的概率减少0.1.
(ⅰ)求乙在前两次挑战中,恰好成功一次的概率;
(ⅱ)求乙在第二次成功的条件下,第三次成功的概率.
您最近一年使用:0次
2022-04-27更新
|
2926次组卷
|
5卷引用:辽宁省大连市2022届高三第一次模拟考试数学试题