名校
解题方法
1 . 三门是“中国青蟹之乡”,气候温暖、港湾平静、水质优良,以优越的自然环境成为我国优质青蟹的最佳产区.所产的三门青蟹具有“金爪、绯钳、青背、黄肚”的特征,以“壳薄、皆黄、肉嫩、味美”而著称,素有“三门青蟹、横行世界”之美誉;且营养丰富,内含人体所需的18种氨基酸和蛋白质、脂肪、钙、磷、铁等营养成分,被誉为“海中黄金,蟹中臻品”.养殖户一般把重量超过350克的青蟹标记为 类青蟹
类青蟹
(1)现有一个小型养蟹池,已知蟹池中有50只青蟹,其中 类青蟹有7只,若从池中抓了2只青蟹,用
类青蟹有7只,若从池中抓了2只青蟹,用 表示其中
表示其中 类青蟹的只数,请写出
类青蟹的只数,请写出 的分布列,并求
的分布列,并求 的数学期望
的数学期望 ;
;
(2)另有一个养蟹池,为估计蟹池中的青蟹数目 ,小王先从中抓了50只青蟹,做好记号后放回池中,过了一段时间后,再从中抓了20只青蟹,发现有记号的有
,小王先从中抓了50只青蟹,做好记号后放回池中,过了一段时间后,再从中抓了20只青蟹,发现有记号的有 只,若
只,若 ,试给出蟹池中青蟹数目
,试给出蟹池中青蟹数目 的估计值(以使
的估计值(以使 取得最大值的
取得最大值的 为估计值).
为估计值).
 类青蟹
类青蟹(1)现有一个小型养蟹池,已知蟹池中有50只青蟹,其中
 类青蟹有7只,若从池中抓了2只青蟹,用
类青蟹有7只,若从池中抓了2只青蟹,用 表示其中
表示其中 类青蟹的只数,请写出
类青蟹的只数,请写出 的分布列,并求
的分布列,并求 的数学期望
的数学期望 ;
;(2)另有一个养蟹池,为估计蟹池中的青蟹数目
 ,小王先从中抓了50只青蟹,做好记号后放回池中,过了一段时间后,再从中抓了20只青蟹,发现有记号的有
,小王先从中抓了50只青蟹,做好记号后放回池中,过了一段时间后,再从中抓了20只青蟹,发现有记号的有 只,若
只,若 ,试给出蟹池中青蟹数目
,试给出蟹池中青蟹数目 的估计值(以使
的估计值(以使 取得最大值的
取得最大值的 为估计值).
为估计值).
您最近一年使用:0次
2023-06-27更新
|
571次组卷
|
3卷引用:浙江省温州市十校联合体2022-2023学年高二下学期期末联考数学试题
浙江省温州市十校联合体2022-2023学年高二下学期期末联考数学试题江西省全南中学2022-2023学年高二下学期期末教学质量验收数学试题(已下线)专题04 超几何分布+二项分布+正态分布压轴题(1)
2 . 李老师从课本上抄录一个随机变量 的分布列如下表:
的分布列如下表:
现让小王同学计算 的数学期望,尽管“?”处的数值完全无法看清,且两个“!”处字迹模糊,但能断定这两个“!”处的数值相同,则
的数学期望,尽管“?”处的数值完全无法看清,且两个“!”处字迹模糊,但能断定这两个“!”处的数值相同,则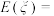 ( )
( )
 的分布列如下表:
的分布列如下表:
| 1 | 2 | 3 |
P | ! | ? | ! |
 的数学期望,尽管“?”处的数值完全无法看清,且两个“!”处字迹模糊,但能断定这两个“!”处的数值相同,则
的数学期望,尽管“?”处的数值完全无法看清,且两个“!”处字迹模糊,但能断定这两个“!”处的数值相同,则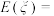 ( )
( )| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
解题方法
3 . 党的二十大报告中提出:“我们要坚持以推动高质量发展为主题,推动经济实现质的有效提升和量的合理增长”.为了适应新形势,满足市场需求,某企业准备购进新型机器以提高生产效益.已知生产产品的质量以其质量指标值 来衡量,并按照质量指标值
来衡量,并按照质量指标值 划分产品等级如图表1:
划分产品等级如图表1:
图表1
现从试用的新机器生产的产品中随机抽取200件作为样品,检验其质量指标值 ,得到频率分布直方图,如图表2:
,得到频率分布直方图,如图表2:

(1)根据样本估计总体的思想,求该产品的质量指标值 的第70百分位数(精确到0.1);
的第70百分位数(精确到0.1);
(2)整理该企业的以往销量数据,获得信息如图表3:
图表3
(产品各等级的销售率为等级产品销量与其对应产量的比值)
已知该企业购进新型机器的前提条件是,该机器生产的产品同时满足下列两个条件:
①质量指标值的平均数(同一组中的数据用该组区间的中点值作代表)不低于35.
②单件产品平均利润不低于4元.
已知该新型机器生产的产品的成本为10元/件,月产量为2000件,根据图表1、图表2、图表3信息,分析该新机器是否达到企业的购进条件.
 来衡量,并按照质量指标值
来衡量,并按照质量指标值 划分产品等级如图表1:
划分产品等级如图表1:图表1
质量指标值 | 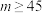 | 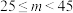 |  |
| 产品等级 | 一等品 | 二等品 | 三等品 |
 ,得到频率分布直方图,如图表2:
,得到频率分布直方图,如图表2:
(1)根据样本估计总体的思想,求该产品的质量指标值
 的第70百分位数(精确到0.1);
的第70百分位数(精确到0.1);(2)整理该企业的以往销量数据,获得信息如图表3:
图表3
| 产品等级 | 一等品 | 二等品 | 三等品 |
| 销售率 | 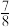 |  |  |
| 单件产品原售价 | 20元 | 15元 | 10元 |
未按原价售出的产品统一按原售价的 可以全部售出 可以全部售出 | |||
已知该企业购进新型机器的前提条件是,该机器生产的产品同时满足下列两个条件:
①质量指标值的平均数(同一组中的数据用该组区间的中点值作代表)不低于35.
②单件产品平均利润不低于4元.
已知该新型机器生产的产品的成本为10元/件,月产量为2000件,根据图表1、图表2、图表3信息,分析该新机器是否达到企业的购进条件.
您最近一年使用:0次
名校
4 . 某一个人在家里积极锻练,等步长沿直线前后连续移步,从点A出发,每次等可能地向前或向后移动一步.
(1)若此人共移动4步,求此人回到点A的概率;
(2)若此人共移动7步到达点M,记A,M两点的距离的步数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1)若此人共移动4步,求此人回到点A的概率;
(2)若此人共移动7步到达点M,记A,M两点的距离的步数为随机变量
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
名校
5 . 某校开展“学习二十大,永远跟党走”网络知识竞赛.每人可参加多轮答题活动,每轮答题情况互不影响.每轮比赛共有两组题,每组都有两道题,只有第一组的两道题均答对,方可进行第二组答题,否则本轮答题结束.已知甲同学第一组每道题答对的概率均为 ,第二组每道题答对的概率均为
,第二组每道题答对的概率均为 ,两组题至少答对3题才可获得一枚纪念章.
,两组题至少答对3题才可获得一枚纪念章.
(1)记甲同学在一轮比赛答对的题目数为 ,请写出
,请写出 的分布列,并求
的分布列,并求 ;
;
(2)若甲同学进行了10轮答题,试问获得多少枚纪念章的概率最大.
 ,第二组每道题答对的概率均为
,第二组每道题答对的概率均为 ,两组题至少答对3题才可获得一枚纪念章.
,两组题至少答对3题才可获得一枚纪念章.(1)记甲同学在一轮比赛答对的题目数为
 ,请写出
,请写出 的分布列,并求
的分布列,并求 ;
;(2)若甲同学进行了10轮答题,试问获得多少枚纪念章的概率最大.
您最近一年使用:0次
2023-05-06更新
|
3181次组卷
|
7卷引用:浙江省温州市2023届高三下学期5月第三次适应性考试(三模)数学试题
浙江省温州市2023届高三下学期5月第三次适应性考试(三模)数学试题湖北省黄冈市浠水县第一中学2022-2023学年高二下学期5月质量检测数学试题(已下线)模块六 专题12 易错题目重组卷(云南卷)(已下线)3.2.3 离散型随机变量的数学期望(同步练习)-【素养提升—课时练】2022-2023学年高二数学湘教版选择性必修第二册检测 (提高篇)山东省烟台市蓬莱区两校2023届高三三模联考数学试题河南省南阳市桐柏县2023-2024学年高二上学期期末质量检测数学试题四川省泸州市泸县第五中学2023-2024学年高二下学期6月月考数学试题
6 . 一个袋子中装有大小相同的5个小球,其中有3个白球,2个红球,小明从中无放回地取出3个小球,摸到一个白球记1分,摸到一个红球记2分,则小明总得分 的数学期望等于( )
的数学期望等于( )
 的数学期望等于( )
的数学期望等于( )| A.3.8分 | B.4分 | C.4.2分 | D.4.4分 |
您最近一年使用:0次
2022-11-11更新
|
1264次组卷
|
3卷引用:浙江省温州市普通高中2023届高三上学期11月第一次适应性考试数学试题
名校
7 . 某贵妃芒是芒果的一种,又名红金龙,是产于海南的一种水果.该芒果按照等级可分为四类:A等级、B等级、C等级和D等级.某采购商打算订购一批芒果销往省外,并从采购的这批芒果中随机抽取100箱(每箱有5kg),利用芒果的等级分类标准得到的数据如下表:
(1)若将频率作为概率,从这100箱芒果中有放回地随机抽取4箱,记这四箱中A等级的箱数为 ,求概率
,求概率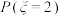 以及
以及 的数学期望;
的数学期望;
(2)利用样本估计总体,果园老板提出两种方案供采购商参考:方案一:不分等级出售,价格为30元/kg;方案二:分等级出售,芒果价格如下表.
从采购商的角度考虑,应该采用哪种方案?
(3)用分层随机抽样的方法从这100箱芒果中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的B等级的箱数,求X的分布列及均值 .
.
等级 | A等级 | B等级 | C等级 | D等级 |
箱数 | 40 | 30 | 20 | 10 |
 ,求概率
,求概率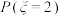 以及
以及 的数学期望;
的数学期望;(2)利用样本估计总体,果园老板提出两种方案供采购商参考:方案一:不分等级出售,价格为30元/kg;方案二:分等级出售,芒果价格如下表.
等级 | A等级 | B等级 | C等级 | D等级 |
价格/(元/kg) | 38 | 32 | 26 | 16 |
(3)用分层随机抽样的方法从这100箱芒果中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的B等级的箱数,求X的分布列及均值
 .
.
您最近一年使用:0次
2022-05-26更新
|
570次组卷
|
4卷引用:浙江省温州市平阳县万全综合高级中学2022-2023学年高二下学期第一次月考数学试题
名校
解题方法
8 . 据调查,目前对于已经近视的小学生,有两种配戴眼镜的选择,一种是佩戴传统的框架眼镜;另一种是佩戴角膜塑形镜,这种眼镜是晚上睡觉时佩戴的一种特殊的隐形眼镜(因其在一定程度上可以减缓近视的发展速度,所以越来越多的小学生家长透择角膜塑形镜控制孩子的近视发展),A市从该地区小学生中随机抽取容量为100的样本,其中因近视佩戴眼镜的有24人(其中佩戴角膜塑形镜的有8人,其中2名是男生,6名是女生)
(1)若从样本中选一位学生,已知这位小学生戴眼镜,那么,他戴的是角膜塑形镜的概率是多大?
(2)从这8名戴角膜塑形镜的学生中,选出3个人,求其中男生人数X的期望与方差;
(3)若将样本的频率当做估计总体的概率,请问,从A市的小学生中,随机选出20位小学生,求佩戴角膜塑形镜的人数Y的期望和方差.
(1)若从样本中选一位学生,已知这位小学生戴眼镜,那么,他戴的是角膜塑形镜的概率是多大?
(2)从这8名戴角膜塑形镜的学生中,选出3个人,求其中男生人数X的期望与方差;
(3)若将样本的频率当做估计总体的概率,请问,从A市的小学生中,随机选出20位小学生,求佩戴角膜塑形镜的人数Y的期望和方差.
您最近一年使用:0次
2022-05-03更新
|
1081次组卷
|
5卷引用:浙江省温州新力量联盟2022-2023学年高二下学期期中联考数学试题



