解题方法
1 . 已知等比数列 的前
的前 项和为
项和为 ,
,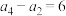 ,
, .数列
.数列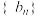 的前
的前 项和为
项和为 ,且
,且 ,
,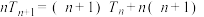 .
.
(1)分别求数列 和
和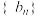 的通项公式;
的通项公式;
(2)若 ,
, 为数列
为数列 的前
的前 项和,是否存在不同的正整数
项和,是否存在不同的正整数 ,
, ,
, (其中
(其中 ,
, ,
, 成等差数列),使得
成等差数列),使得 ,
,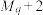 ,
, 成等比数列?若存在,求出所有满足条件的
成等比数列?若存在,求出所有满足条件的 ,
, ,
, 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 的前
的前 项和为
项和为 ,
,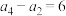 ,
, .数列
.数列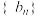 的前
的前 项和为
项和为 ,且
,且 ,
,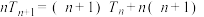 .
.(1)分别求数列
 和
和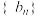 的通项公式;
的通项公式;(2)若
 ,
, 为数列
为数列 的前
的前 项和,是否存在不同的正整数
项和,是否存在不同的正整数 ,
, ,
, (其中
(其中 ,
, ,
, 成等差数列),使得
成等差数列),使得 ,
,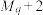 ,
, 成等比数列?若存在,求出所有满足条件的
成等比数列?若存在,求出所有满足条件的 ,
, ,
, 的值;若不存在,说明理由.
的值;若不存在,说明理由.
您最近一年使用:0次
2021-01-31更新
|
561次组卷
|
5卷引用:专题09 《数列》中的存在性问题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)
(已下线)专题09 《数列》中的存在性问题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)山东省烟台市2020-2021学年高二上学期期末数学试题江西省新余市2021-2022学年高二上学期期末数学(理)试题2023版 湘教版(2019) 选修第一册 过关斩将 第1章 综合拔高练(已下线)广东省2022届高三一模数学试题变式题17-22
2 . (1)已知 ,
, .求证:
.求证: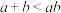 ;
;
(2)在 中,内角
中,内角 的对边分别为
的对边分别为 .若
.若 ,用反证法证明:
,用反证法证明: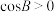 .
.
 ,
, .求证:
.求证: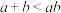 ;
;(2)在
 中,内角
中,内角 的对边分别为
的对边分别为 .若
.若 ,用反证法证明:
,用反证法证明: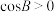 .
.
您最近一年使用:0次
2021-04-30更新
|
287次组卷
|
4卷引用:专题02 推理与证明-2020-2021学年高二数学下学期期末专项复习(苏教版选修2-2、2-3)
(已下线)专题02 推理与证明-2020-2021学年高二数学下学期期末专项复习(苏教版选修2-2、2-3)(已下线)江西省萍乡市2020—2021学年度第二学期期中考试数学(理)试题(已下线)2.2.2 间接证明(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)(已下线)2.2.2 间接证明(基础练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-2)
名校
解题方法
3 . 已知函数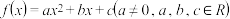 .
.
(1)若 ,且
,且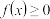 在区间
在区间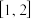 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)当 ,
,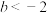 时,求证:在区间
时,求证:在区间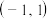 至少存在一个
至少存在一个 ,使得
,使得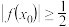 .
.
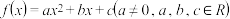 .
.(1)若
 ,且
,且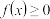 在区间
在区间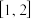 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)当
 ,
,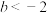 时,求证:在区间
时,求证:在区间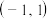 至少存在一个
至少存在一个 ,使得
,使得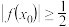 .
.
您最近一年使用:0次
4 . (1)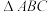 三内角
三内角 成等差数列,对边分别为
成等差数列,对边分别为 .证明:
.证明: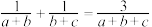 .
.
(2)已知二次函数 的图象与
的图象与 轴有两个不同的交点,
轴有两个不同的交点,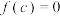 ,当
,当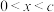 时,
时, .用反证法证明:
.用反证法证明: .
.
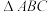 三内角
三内角 成等差数列,对边分别为
成等差数列,对边分别为 .证明:
.证明: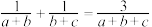 .
.(2)已知二次函数
 的图象与
的图象与 轴有两个不同的交点,
轴有两个不同的交点,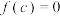 ,当
,当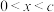 时,
时, .用反证法证明:
.用反证法证明: .
.
您最近一年使用:0次
2021-04-30更新
|
224次组卷
|
4卷引用:专题02 推理与证明-2020-2021学年高二数学下学期期末专项复习(苏教版选修2-2、2-3)
(已下线)专题02 推理与证明-2020-2021学年高二数学下学期期末专项复习(苏教版选修2-2、2-3)(已下线)江西省萍乡市2020—2021学年度第二学期期中考试数学(文)试题(已下线)2.2.2 间接证明(重点练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)(已下线)2.2.2 间接证明(重点练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-2)
5 . 列三角形数表
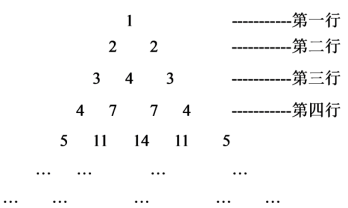
假设第 行的第二个数为
行的第二个数为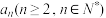
(1)归纳出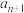 与
与 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;
(2)求证:数列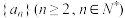 中任意的连续三项不可能构成等差数列.
中任意的连续三项不可能构成等差数列.

假设第
 行的第二个数为
行的第二个数为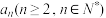
(1)归纳出
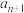 与
与 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;(2)求证:数列
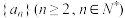 中任意的连续三项不可能构成等差数列.
中任意的连续三项不可能构成等差数列.
您最近一年使用:0次
2021-08-02更新
|
187次组卷
|
2卷引用:江苏省苏州市常熟中学2021-2022学年高二上学期10月阶段学习质量检测数学试题
名校
解题方法
6 . 已知 ,关于
,关于 的方程
的方程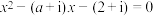 .(
.( 是虚数单位)
是虚数单位)
(1)若方程有实数根,求实数 ;
;
(2)证明:方程无纯虚数根.
 ,关于
,关于 的方程
的方程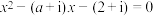 .(
.( 是虚数单位)
是虚数单位)(1)若方程有实数根,求实数
 ;
;(2)证明:方程无纯虚数根.
您最近一年使用:0次



