名校
解题方法
1 . 复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受.形如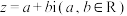 的数称为复数,其中
的数称为复数,其中 称为实部,
称为实部, 称为虚部,i称为虚数单位,
称为虚部,i称为虚数单位, .当
.当 时,
时, 为实数;当
为实数;当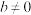 且时,
且时, 为纯虚数.其中
为纯虚数.其中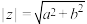 ,叫做复数
,叫做复数 的模.设
的模.设 ,
,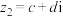 ,
, ,
, ,
, ,
, ,
, 如图,点
如图,点 ,复数
,复数 可用点
可用点 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,
表示,这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数
轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数 都可以表示成
都可以表示成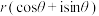 的形式,即
的形式,即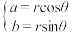 ,其中
,其中 为复数
为复数 的模,
的模, 叫做复数
叫做复数 的辐角,我们规定
的辐角,我们规定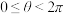 范围内的辐角
范围内的辐角 的值为辐角的主值,记作
的值为辐角的主值,记作 .
.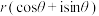 叫做复数
叫做复数 的三角形式.
的三角形式.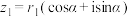 ,
,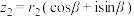 ,求
,求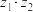 、
、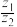 的三角形式;
的三角形式;
(2)设复数 ,
,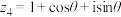 ,其中
,其中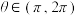 ,求
,求 ;
;
(3)在 中,已知
中,已知 、
、 、
、 为三个内角
为三个内角 的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
① ;
;
②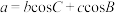 ,
,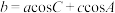 ,
,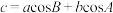 .
.
注意:使用复数以外的方法证明不给分.
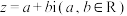 的数称为复数,其中
的数称为复数,其中 称为实部,
称为实部, 称为虚部,i称为虚数单位,
称为虚部,i称为虚数单位, .当
.当 时,
时, 为实数;当
为实数;当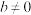 且时,
且时, 为纯虚数.其中
为纯虚数.其中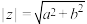 ,叫做复数
,叫做复数 的模.设
的模.设 ,
,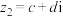 ,
, ,
, ,
, ,
, ,
, 如图,点
如图,点 ,复数
,复数 可用点
可用点 表示,这个建立了直角坐标系来表示复数的平面叫做复平面,
表示,这个建立了直角坐标系来表示复数的平面叫做复平面, 轴叫做实轴,
轴叫做实轴, 轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数
轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.按照这种表示方法,每一个复数,有复平面内唯一的一个点和它对应,反过来,复平面内的每一个点,有唯一的一个复数和它对应.一般地,任何一个复数 都可以表示成
都可以表示成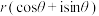 的形式,即
的形式,即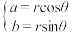 ,其中
,其中 为复数
为复数 的模,
的模, 叫做复数
叫做复数 的辐角,我们规定
的辐角,我们规定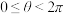 范围内的辐角
范围内的辐角 的值为辐角的主值,记作
的值为辐角的主值,记作 .
.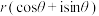 叫做复数
叫做复数 的三角形式.
的三角形式.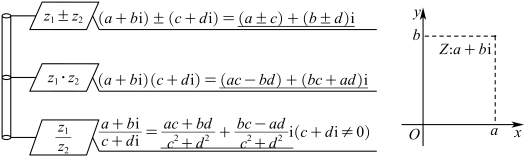
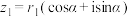 ,
,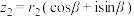 ,求
,求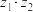 、
、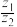 的三角形式;
的三角形式;(2)设复数
 ,
,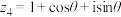 ,其中
,其中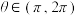 ,求
,求 ;
;(3)在
 中,已知
中,已知 、
、 、
、 为三个内角
为三个内角 的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:
的对应边.借助平面直角坐标系及阅读材料中所给复数相关内容,证明:①
 ;
;②
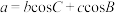 ,
,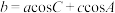 ,
,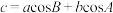 .
.注意:使用复数以外的方法证明不给分.
您最近一年使用:0次
2024-03-12更新
|
580次组卷
|
4卷引用:黑龙江省哈尔滨师范大学附属中学2023-2024学年高一下学期开学考试数学试卷
黑龙江省哈尔滨师范大学附属中学2023-2024学年高一下学期开学考试数学试卷(已下线)模块五 专题六 全真拔高模拟2(已下线)第七章:复数(新题型)-同步精品课堂(人教A版2019必修第二册)重庆市缙云教育联盟2023-2024学年高一下学期3月月度质量检测数学试题
2 . 对于无穷数列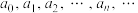 ,我们称
,我们称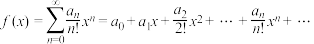 (规定
(规定 )为无穷数列
)为无穷数列 的指数型母函数.无穷数列1,1,…,1,…的指数型母函数记为
的指数型母函数.无穷数列1,1,…,1,…的指数型母函数记为 ,它具有性质
,它具有性质 .
.
(1)证明: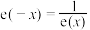 ;
;
(2)记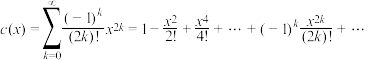 .证明:
.证明: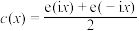 (其中i为虚数单位);
(其中i为虚数单位);
(3)以函数 为指数型母函数生成数列
为指数型母函数生成数列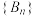 ,
, .其中
.其中 称为伯努利数.证明:
称为伯努利数.证明: .且
.且 .
.
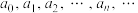 ,我们称
,我们称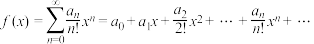 (规定
(规定 )为无穷数列
)为无穷数列 的指数型母函数.无穷数列1,1,…,1,…的指数型母函数记为
的指数型母函数.无穷数列1,1,…,1,…的指数型母函数记为 ,它具有性质
,它具有性质 .
.(1)证明:
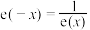 ;
;(2)记
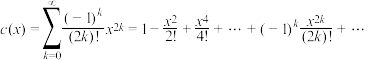 .证明:
.证明: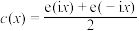 (其中i为虚数单位);
(其中i为虚数单位);(3)以函数
 为指数型母函数生成数列
为指数型母函数生成数列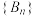 ,
, .其中
.其中 称为伯努利数.证明:
称为伯努利数.证明: .且
.且 .
.
您最近一年使用:0次
2024-03-03更新
|
555次组卷
|
3卷引用:压轴题06向量、复数压轴题16题型汇总-2
3 . 通过平面直角坐标系,我们可以用有序实数对表示向量.类似的,我们可以把有序复数对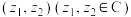 看作一个向量,记
看作一个向量,记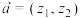 ,则称
,则称 为复向量.类比平面向量的相关运算法则,对于
为复向量.类比平面向量的相关运算法则,对于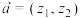 ,
,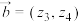 ,
, 、
、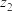 、
、 、
、 、
、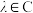 ,我们有如下运算法则:
,我们有如下运算法则:
①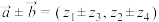 ; ②
; ② ;
;
③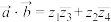 ; ④
; ④ .
.
(1)设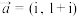 ,
,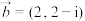 ,求
,求 和
和 .
.
(2)由平面向量的数量积满足的运算律,我们类比得到复向量的相关结论:
①
② ③
③ .
.
试判断这三个结论是否正确,并对正确的结论予以证明.
(3)若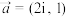 ,集合
,集合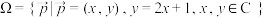 ,
,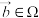 .对于任意的
.对于任意的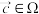 ,求出满足条件
,求出满足条件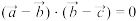 的
的 ,并将此时的
,并将此时的 记为
记为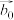 ,证明对任意的
,证明对任意的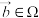 ,不等式
,不等式 恒成立.
恒成立.
根据对上述问题的解答过程,试写出一个一般性的命题(不需要证明).
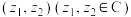 看作一个向量,记
看作一个向量,记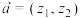 ,则称
,则称 为复向量.类比平面向量的相关运算法则,对于
为复向量.类比平面向量的相关运算法则,对于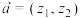 ,
,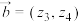 ,
, 、
、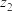 、
、 、
、 、
、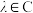 ,我们有如下运算法则:
,我们有如下运算法则:①
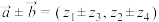 ; ②
; ② ;
;③
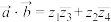 ; ④
; ④ .
.(1)设
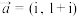 ,
,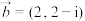 ,求
,求 和
和 .
.(2)由平面向量的数量积满足的运算律,我们类比得到复向量的相关结论:
①

②
 ③
③ .
.试判断这三个结论是否正确,并对正确的结论予以证明.
(3)若
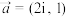 ,集合
,集合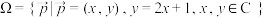 ,
,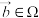 .对于任意的
.对于任意的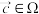 ,求出满足条件
,求出满足条件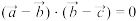 的
的 ,并将此时的
,并将此时的 记为
记为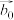 ,证明对任意的
,证明对任意的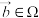 ,不等式
,不等式 恒成立.
恒成立.根据对上述问题的解答过程,试写出一个一般性的命题(不需要证明).
您最近一年使用:0次
2023-07-06更新
|
543次组卷
|
7卷引用:上海市闵行区2022-2023学年高一下学期期末数学试题
上海市闵行区2022-2023学年高一下学期期末数学试题(已下线)专题7.4 复数运算的综合应用大题专项训练-举一反三系列-(已下线)第06讲 第七章 复数 章节验收测评卷-【帮课堂】(人教A版2019必修第二册)(已下线)专题06 期末解答压轴题-《期末真题分类汇编》(上海专用)(已下线)专题03 复数-《期末真题分类汇编》(人教A版2019必修第二册)(已下线)专题01 复数-《期末真题分类汇编》(上海专用)(已下线)第12章 复数单元综合能力测试卷-【帮课堂】(苏教版2019必修第二册)
4 . 利用平面向量的坐标表示,可以把平面向量的概念推广为坐标为复数的“复向量”,即可将有序复数对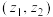 (其中
(其中 )视为一个向量,记作
)视为一个向量,记作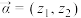 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量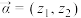 ,
,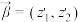 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足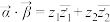 ,复向量
,复向量 的模定义为
的模定义为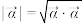 .
.
(1)设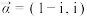 ,
, ,
, 为虚数单位,求复向量
为虚数单位,求复向量 、
、 的模;
的模;
(2)设 、
、 是两个复向量,
是两个复向量,
①已知对于任意两个平面向量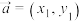 ,
,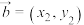 ,(其中
,(其中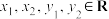 ),
), 成立,证明:对于复向量
成立,证明:对于复向量 、
、 ,
, 也成立;
也成立;
②当 时,称复向量
时,称复向量 与
与 平行.若复向量
平行.若复向量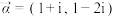 与
与 平行(其中
平行(其中 为虚数单位,
为虚数单位,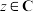 ),求复数
),求复数 .
.
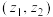 (其中
(其中 )视为一个向量,记作
)视为一个向量,记作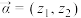 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量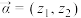 ,
,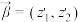 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足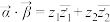 ,复向量
,复向量 的模定义为
的模定义为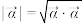 .
.(1)设
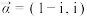 ,
, ,
, 为虚数单位,求复向量
为虚数单位,求复向量 、
、 的模;
的模;(2)设
 、
、 是两个复向量,
是两个复向量,①已知对于任意两个平面向量
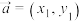 ,
,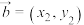 ,(其中
,(其中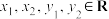 ),
), 成立,证明:对于复向量
成立,证明:对于复向量 、
、 ,
, 也成立;
也成立;②当
 时,称复向量
时,称复向量 与
与 平行.若复向量
平行.若复向量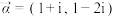 与
与 平行(其中
平行(其中 为虚数单位,
为虚数单位,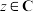 ),求复数
),求复数 .
.
您最近一年使用:0次
2023-07-04更新
|
817次组卷
|
14卷引用:上海市上海中学2022-2023学年高一下学期期末数学试题
上海市上海中学2022-2023学年高一下学期期末数学试题(已下线)专题7.6 复数全章八大压轴题型归纳(拔尖篇)--举一反三系列-(已下线)专题7.4 复数运算的综合应用大题专项训练-举一反三系列-(已下线)专题03 与复数有关的压轴题-【常考压轴题】(已下线)专题11+复数的四则运算(2)-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)7.2.2复数的乘、除运算——课后作业(提升版)单元测试B卷——第七章 复数(已下线)第9章 复数(单元测试卷)-同步精品课堂(沪教版2020必修第二册)(已下线)9.2 复数的几何意义-同步精品课堂(沪教版2020必修第二册)(已下线)专题06 期末解答压轴题-《期末真题分类汇编》(上海专用)(已下线)期末测试卷03-《期末真题分类汇编》(上海专用)(已下线)专题03 复数-《期末真题分类汇编》(人教A版2019必修第二册)(已下线)上海市高一下学期期末真题必刷04-期末考点大串讲(沪教版2020必修二)安徽省安庆市第一中学2023-2024学年高一下学期5月同步测试数学试卷
名校
5 . 利用平面向量的坐标表示,可以把平面向量的概念推广为坐标为复数的“复向量”,即可将有序复数对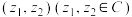 视为一个向量,记作
视为一个向量,记作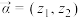 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量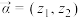 ,
,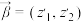 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足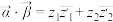 ,复向量
,复向量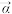 的模定义为
的模定义为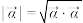 .
.
(1)设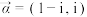 ,
,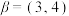 ,求复向量
,求复向量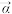 ,
,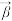 的模;
的模;
(2)设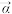 、
、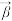 是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即:
是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即: ;
;
(3)当 时,称复向量
时,称复向量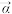 与
与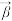 平行.设
平行.设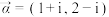 、
、 ,若复向量
,若复向量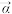 与
与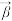 平行,求复数
平行,求复数 的值.
的值.
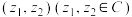 视为一个向量,记作
视为一个向量,记作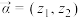 .类比平面向量可以定义其运算,两个复向量
.类比平面向量可以定义其运算,两个复向量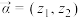 ,
,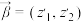 的数量积定义为一个复数,记作
的数量积定义为一个复数,记作 ,满足
,满足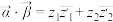 ,复向量
,复向量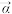 的模定义为
的模定义为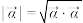 .
.(1)设
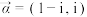 ,
,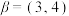 ,求复向量
,求复向量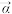 ,
,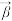 的模;
的模;(2)设
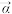 、
、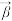 是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即:
是两个复向量,证明柯西一布涅科夫斯基不等式仍成立,即: ;
;(3)当
 时,称复向量
时,称复向量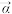 与
与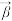 平行.设
平行.设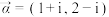 、
、 ,若复向量
,若复向量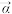 与
与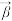 平行,求复数
平行,求复数 的值.
的值.
您最近一年使用:0次
2021-07-12更新
|
1266次组卷
|
9卷引用:上海交通大学附属中学2020-2021学年高一下学期期末数学试题
上海交通大学附属中学2020-2021学年高一下学期期末数学试题(已下线)7.2复数的四则运算C卷(已下线)专题05 复数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)(已下线)第02讲 复数的运算-【帮课堂】2021-2022学年高一数学同步精品讲义(苏教版2019必修第二册)高一复数重难点提高卷-【同步题型讲义】(已下线)第七章 复数(基础、典型、易错、压轴)分类专项训练(2)(已下线)复数的概念与运算(已下线)第7章 复数-《重难点题型·高分突破》(人教A版2019必修第二册)第12章 复数(单元测试)-2022-2023学年高一数学同步精品课堂(苏教版2019必修第二册)
2021高三·全国·专题练习
解题方法
6 . 设复平面上点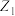 ,
,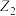 ,…,
,…, ,…分别对应复数
,…分别对应复数 ,
,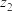 ,…,
,…, ,…
,…
(1)设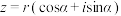 ,(
,( ,
, ),用数学归纳法证明:
),用数学归纳法证明: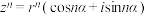 ,
,
(2)已知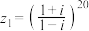 ,且
,且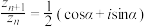 (
( 为实常数),求出数列
为实常数),求出数列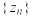 的通项公式;
的通项公式;
(3)在(2)的条件下,求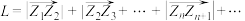 .
.
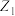 ,
,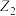 ,…,
,…, ,…分别对应复数
,…分别对应复数 ,
,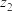 ,…,
,…, ,…
,…(1)设
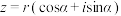 ,(
,( ,
, ),用数学归纳法证明:
),用数学归纳法证明: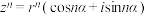 ,
,
(2)已知
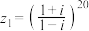 ,且
,且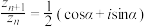 (
( 为实常数),求出数列
为实常数),求出数列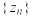 的通项公式;
的通项公式; (3)在(2)的条件下,求
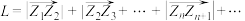 .
.
您最近一年使用:0次
7 . 求证:
(1)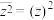 ;
;
(2) ;
;
(3)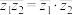 ;
;
(4)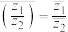 .
.
(1)
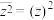 ;
;(2)
 ;
;(3)
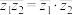 ;
;(4)
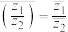 .
.
您最近一年使用:0次
2020-01-30更新
|
1267次组卷
|
6卷引用:人教B版(2019) 必修第四册 逆袭之路 第十章 10.2.2 复数的乘法与除法
人教B版(2019) 必修第四册 逆袭之路 第十章 10.2.2 复数的乘法与除法(已下线)第19讲压轴综合题(讲义)-【教育机构专用】2021年春季高一数学辅导讲义(沪教版2020必修第二册)(已下线)第十章 复数 10.2 复数的运算 10.2.2 复数的乘法与除法(已下线)专题05 复数压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)人教B版(2019)必修第四册课本习题10.2.2 复数的乘法与除法(已下线)第七章 复数(基础、典型、易错、压轴)分类专项训练(2)
8 . 关于复数z的方程z2-(a+i)z-(i+2)=0(a∈R).
(1)若此方程有实数解,求a的值;
(2)用反证法证明:对任意的实数a,原方程不可能有纯虚数根.
(1)若此方程有实数解,求a的值;
(2)用反证法证明:对任意的实数a,原方程不可能有纯虚数根.
您最近一年使用:0次
9 . 已知 是虚数,
是虚数,  是实数.
是实数.
(1)求 为何值时,
为何值时, 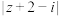 有最小值,并求出|
有最小值,并求出|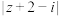 的最小值;
的最小值;
(2)设 ,求证:
,求证:  为纯虚数.
为纯虚数.
 是虚数,
是虚数,  是实数.
是实数.(1)求
 为何值时,
为何值时, 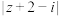 有最小值,并求出|
有最小值,并求出|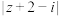 的最小值;
的最小值;(2)设
 ,求证:
,求证:  为纯虚数.
为纯虚数.
您最近一年使用:0次
2017-05-21更新
|
2183次组卷
|
4卷引用:安徽省定远重点中学2017-2018学年高二下学期教学段考数学(理)试题
安徽省定远重点中学2017-2018学年高二下学期教学段考数学(理)试题(已下线)专题16 复数——常见中档题型汇编-【重难点突破】2021-2022学年高一数学常考题专练(人教A版2019必修第二册)江苏省江阴市四校2016-2017学年高二下学期期中考试数学(理)试题江苏省苏州市吴中区2018-2019学年高二下学期期中数学(理)试题



