1 . 设z是虚数, 是实数,且
是实数,且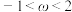 .
.
(1)求z的实部的取值范围;
(2)设 ,求证:u为纯虚数.
,求证:u为纯虚数.
 是实数,且
是实数,且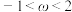 .
.(1)求z的实部的取值范围;
(2)设
 ,求证:u为纯虚数.
,求证:u为纯虚数.
您最近一年使用:0次
2 . 已知复数 满足
满足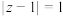 .
.
(1)求 的最小值与最大值;
的最小值与最大值;
(2)若 是虚数,且
是虚数,且 为实数,求证:
为实数,求证: .
.
 满足
满足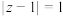 .
.(1)求
 的最小值与最大值;
的最小值与最大值;(2)若
 是虚数,且
是虚数,且 为实数,求证:
为实数,求证: .
.
您最近一年使用:0次
10-11高二下·河南郑州·阶段练习
名校
解题方法
3 . 设 是虚数,且
是虚数,且 满足
满足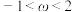 .
.
(1)求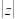 的值及
的值及 的实部的取值范围;
的实部的取值范围;
(2)设 ,求证:
,求证: 为纯虚数;
为纯虚数;
(3)求 的最小值.
的最小值.
 是虚数,且
是虚数,且 满足
满足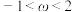 .
.(1)求
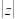 的值及
的值及 的实部的取值范围;
的实部的取值范围;(2)设
 ,求证:
,求证: 为纯虚数;
为纯虚数;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
2022-03-21更新
|
1426次组卷
|
28卷引用:2010-2011年河南省郑州市第47中学高二下学期第一次月考数学文卷
(已下线)2010-2011年河南省郑州市第47中学高二下学期第一次月考数学文卷河南省兰考县第二高级中学人教版高二数学选修2-2单元测试:第三章数系的扩充与复数的引入(已下线)2012年苏教版高中数学选修2-2 3.2复数的四则运算练习卷(已下线)2013-2014学年江西省吉安一中高二下学期期中考试文科数学试卷黑龙江省海林市朝鲜族中学人教版高中数学选修1-2同步练习:滚动习题第三章 数系的扩充与复数的引入[范围3.1~3.2]上海市宝山区宝山中学2017-2018学年高二下学期3月月考数学试题人教A版(2019) 必修第二册 过关斩将 第七章 7.3 复数的三角表示沪教版(上海) 高二第二学期 新高考辅导与训练 第13章 复数 本章复习题(已下线)专题59 复数(同步练习)-2021年高考一轮数学(文)单元复习一遍过(已下线)专题65 复数(同步练习)-2021年高考一轮数学单元复习一遍过(新高考地区专用)(已下线)专题65 复数(同步练习)-2021年高考一轮数学(理)单元复习一遍过江苏省新区实验2020-2021学年高一下学期期中数学试题重庆市第八中学2020-2021学年高一下学期第三次月考数学试题江苏省苏州市实验中学2020-2021学年高一下学期期中数学试题(已下线)专题7.3 复数 章末检测3(难)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(人教A版2019必修第二册)(已下线)第七章 复数(基础训练)A卷-2021-2022学年高一数学课后培优练(人教A版2019必修第二册)苏教版(2019) 必修第二册 过关斩将 第12章 本章达标检测沪教版(2020) 一轮复习 堂堂清 第六单元 6.4 复数的运算天津市第四十二中学2019-2020学年高一下学期期中理科数学试题广东省广州市真光中学2022-2023学年高一下学期期中数学试题3.2复数的四则运算(已下线)专题11+复数的四则运算(2)-《重难点题型·高分突破》(人教A版2019必修第二册)陕西省咸阳市永寿县中学2023-2024学年高一下学期第一次月考(3月)数学试题(已下线)7.3复数的三角表示——课后作业(提升版)(已下线)7.3复数的三角表示——课后作业(巩固版)(已下线)复数-综合测试卷A卷内蒙古通辽市科尔沁左翼中旗实验高级中学2023-2024学年高一下学期期中考试数学试题【巩固卷】章末检测试卷(三)单元测试A-湘教版(2019)必修(第二册)
4 . 设z是虚数,ω=z+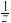 是实数,且-1<ω<2.
是实数,且-1<ω<2.
(1)求|z|的值及z的实部的取值范围;
(2)设μ= ,求证:μ为纯虚数.
,求证:μ为纯虚数.
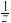 是实数,且-1<ω<2.
是实数,且-1<ω<2.(1)求|z|的值及z的实部的取值范围;
(2)设μ=
 ,求证:μ为纯虚数.
,求证:μ为纯虚数.
您最近一年使用:0次
2022-02-22更新
|
940次组卷
|
10卷引用:2014-2015学年河南实验中学高二下学期期中理科数学试卷
2014-2015学年河南实验中学高二下学期期中理科数学试卷河北省唐山市玉田县2018-2019学年高二下学期期中数学(文)试题江苏省宿迁市宿豫中学2019-2020学年高二(奥赛班)下学期4月月考数学试题山东省滕州市第一中学2019-2020学年高一5月摸底考试数学试题(已下线)【新教材精创】10.2.2复数的乘法与除法练习(2)(已下线)3.2 复数的四则运算(已下线)期中模拟卷-2021-2022学年高一数学链接教材精准变式练(人教A版2019必修第二册)(已下线)第12章 复数(综合测试卷)-2021-2022学年高一数学10分钟课前预习练(苏教版2019必修第二册)(已下线)专题02 复数的四则运算-2021-2022学年高一《新题速递·数学》(人教A版2019)湖南省长沙市长郡中学2021-2022学年高一下学期期末数学试题
5 . 已知复数 的模为
的模为 .
.
(1)写出一个 ,使得
,使得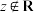 ,但
,但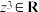 (只需要写出一个
(只需要写出一个 ,无需证明);
,无需证明);
(2)设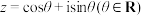 ,
,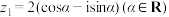 ,分别求
,分别求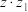 ,
,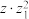 ,
, 的实部(用
的实部(用 ,
, 表示),并归纳得出
表示),并归纳得出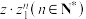 的实部.
的实部.
 的模为
的模为 .
.(1)写出一个
 ,使得
,使得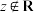 ,但
,但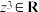 (只需要写出一个
(只需要写出一个 ,无需证明);
,无需证明);(2)设
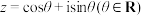 ,
,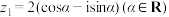 ,分别求
,分别求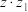 ,
,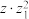 ,
, 的实部(用
的实部(用 ,
, 表示),并归纳得出
表示),并归纳得出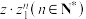 的实部.
的实部.
您最近一年使用:0次
9-10高二下·陕西西安·期中
名校
解题方法
6 . 设 是虚数,
是虚数, 是实数,且
是实数,且 .
.
(1)求|z1|的值以及z1的实部的取值范围.
(2)若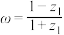 ,求证:
,求证: 为纯虚数.
为纯虚数.
 是虚数,
是虚数, 是实数,且
是实数,且 .
.(1)求|z1|的值以及z1的实部的取值范围.
(2)若
 ,求证:
,求证: 为纯虚数.
为纯虚数.
您最近一年使用:0次
2016-11-30更新
|
2172次组卷
|
20卷引用:2010年河南省实验中学高二下学期期中考试数学(理)
(已下线)2010年河南省实验中学高二下学期期中考试数学(理)(已下线)2010年河南省实验中学高二下学期期中考试数学(文)(已下线)2010年陕西省西安市铁一中高二下学期期中考试数学(文)(已下线)2012-2013学年浙江省台州中学高二下学期期中文科数学试卷2016-2017学年山东省临沂第一中学高二下学期第一次月考数学(理)试卷高中数学人教A版选修2-2 第三章 数系的扩充与复数的引入 3.2.2 复数代数形式的乘除运算 (1)山西省运城市康杰中学2017-2018学年高二下学期期中考试数学(理)试题【全国百强校】宁夏育才中学2017-2018学年高二下学期期中考试数学(文)试题(已下线)2019年3月24日 《每日一题》文数选修1-2-每周一测(已下线)2019年4月14日 《每日一题》理数选修2-2(期中复习)-每周一测山西省晋中市平遥中学2018-2019学年高二下学期期中考试数学(理)试题上海市十二校2017届高三上学期12月联考数学试题浙江省宁波市北仑中学2019-2020学年高一(1班)下学期期中数学试题(已下线)第30讲 复数-2021年新高考数学一轮专题复习(新高考专版)(已下线)第07章+复数(B卷提高篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版)(已下线)12.6 复数综合练习(提优)-2020-2021学年高一数学同步课堂帮帮帮(苏教版2019必修第二册)河北省尚义县第一中学2020-2021学年高二下学期期中数学试题(已下线)专题7.3 复数 章末检测3(难)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(人教A版2019必修第二册)(已下线)第七章 复数单元自测卷(二)第5章 复数 单元测试题2020-2021学年高一下学期数学北师大版(2019)必修第二册



