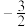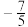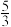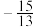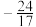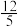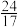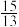1 . 综合与实践:
《函数》复习课后,为加深对函数的认识,张老师引导同学们对函数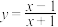 的图象与性质进行探究.过程如下,请完成探究过程:
的图象与性质进行探究.过程如下,请完成探究过程:
(1)初步感知
函数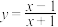 的自变量取值范围是______;
的自变量取值范围是______;
(2)作出图象
①列表:
填空:表中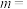 ______,
______, ______;
______;
②描点,连线:
在平面直角坐标系 中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
小刚观察图象,发现这个图象为双曲线,进一步研究中,小刚将函数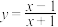 转化为
转化为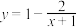 ,他判断该函数图象就是反比例函数
,他判断该函数图象就是反比例函数 通过某种平移转化而来,反比例函数
通过某种平移转化而来,反比例函数 的图象是中心对称图形,对称中心为
的图象是中心对称图形,对称中心为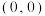 ,则函数
,则函数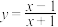 的图象的对称中心为______;反比例函数
的图象的对称中心为______;反比例函数 的图象是轴对称图形,对称轴为直线
的图象是轴对称图形,对称轴为直线 和
和 ,则函数
,则函数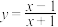 的图象的对称轴为直线______
的图象的对称轴为直线______
(4)拓展应用
①若一次函数 的图象与函数
的图象与函数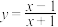 的图象交于A、B两点,连接
的图象交于A、B两点,连接 ,则
,则 的面积为______
的面积为______
②若直线 与函数
与函数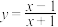 的图象有且只有一个交点,则k的值为______.
的图象有且只有一个交点,则k的值为______.
《函数》复习课后,为加深对函数的认识,张老师引导同学们对函数
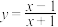 的图象与性质进行探究.过程如下,请完成探究过程:
的图象与性质进行探究.过程如下,请完成探究过程:(1)初步感知
函数
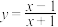 的自变量取值范围是______;
的自变量取值范围是______;(2)作出图象
①列表:
x | … |
|
|
|
|
|
|
|
| n |
| 0 | 1 | 2 | 3 | 4 | … |
y | … |
|
|
| 2 | 3 | 4 | m | 6 |
|
|
| 0 |
|
|
| … |
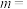 ______,
______, ______;
______;②描点,连线:
在平面直角坐标系
 中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;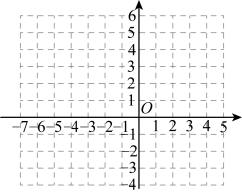
小刚观察图象,发现这个图象为双曲线,进一步研究中,小刚将函数
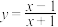 转化为
转化为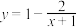 ,他判断该函数图象就是反比例函数
,他判断该函数图象就是反比例函数 通过某种平移转化而来,反比例函数
通过某种平移转化而来,反比例函数 的图象是中心对称图形,对称中心为
的图象是中心对称图形,对称中心为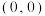 ,则函数
,则函数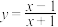 的图象的对称中心为______;反比例函数
的图象的对称中心为______;反比例函数 的图象是轴对称图形,对称轴为直线
的图象是轴对称图形,对称轴为直线 和
和 ,则函数
,则函数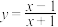 的图象的对称轴为直线______
的图象的对称轴为直线______(4)拓展应用
①若一次函数
 的图象与函数
的图象与函数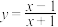 的图象交于A、B两点,连接
的图象交于A、B两点,连接 ,则
,则 的面积为______
的面积为______②若直线
 与函数
与函数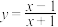 的图象有且只有一个交点,则k的值为______.
的图象有且只有一个交点,则k的值为______.
您最近一年使用:0次
2 . 在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数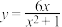 的性质及其应用的部分过程,请按要求完成下列各小题.
的性质及其应用的部分过程,请按要求完成下列各小题.
(1)请把下表补充完整,并在图中补全该函数图象.
①该函数图象是轴对称图形,它的对称轴为y轴.
②该函数在自变量的取值范围内,有最大值和最小值.当 时,函数取得最大值3;当
时,函数取得最大值3;当 时,函数取得最小值
时,函数取得最小值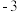 .
.
③当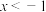 或
或 时,y随x的增大而减小;当
时,y随x的增大而减小;当 时,y随x的增大而增大.
时,y随x的增大而增大.
(3)若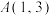 ,
, ,
,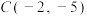 ,直接写出
,直接写出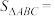 .
.
(4)已知函数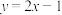 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式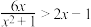 的解集(保留1位小数,误差不超过0.2).
的解集(保留1位小数,误差不超过0.2).
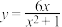 的性质及其应用的部分过程,请按要求完成下列各小题.
的性质及其应用的部分过程,请按要求完成下列各小题.(1)请把下表补充完整,并在图中补全该函数图象.
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
| 0 | 3 |
|
|
| … |
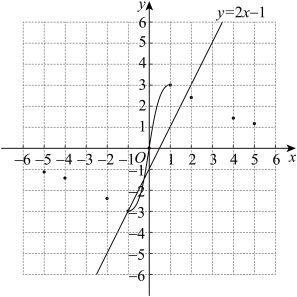
①该函数图象是轴对称图形,它的对称轴为y轴.
②该函数在自变量的取值范围内,有最大值和最小值.当
 时,函数取得最大值3;当
时,函数取得最大值3;当 时,函数取得最小值
时,函数取得最小值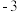 .
.③当
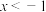 或
或 时,y随x的增大而减小;当
时,y随x的增大而减小;当 时,y随x的增大而增大.
时,y随x的增大而增大.(3)若
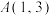 ,
, ,
,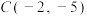 ,直接写出
,直接写出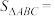 .
.(4)已知函数
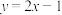 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式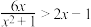 的解集(保留1位小数,误差不超过0.2).
的解集(保留1位小数,误差不超过0.2).
您最近一年使用:0次
名校
3 . 有这样一个问题:探究函数y=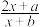 的图象与性质,小童根据学习函数的经验,对函数的图象与性质进行例研究,已知当x=2时,y=7,
的图象与性质,小童根据学习函数的经验,对函数的图象与性质进行例研究,已知当x=2时,y=7, 时,y=﹣3.下面是小童探究的过程,请补充完整:
时,y=﹣3.下面是小童探究的过程,请补充完整:
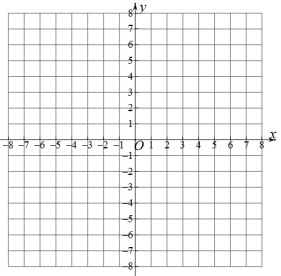
(1)该函数的解析式为 ,m= ,n= .
根据图中描出的点,画出函数图象.
(2)根据函图象,下列关于函数性质的描述正确的是 ;
①该函数图象是中心对称图形,它的对称中心是原点.
②该函数既无最大值也无最小值.
③在自变量的取值范围内,y随x的增大而减小.
(3)请结合(1)中函数图象,直接写出关于x的不等式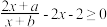 的解集.(保留1位小数,误差不超过0.2)
的解集.(保留1位小数,误差不超过0.2)
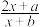 的图象与性质,小童根据学习函数的经验,对函数的图象与性质进行例研究,已知当x=2时,y=7,
的图象与性质,小童根据学习函数的经验,对函数的图象与性质进行例研究,已知当x=2时,y=7, 时,y=﹣3.下面是小童探究的过程,请补充完整:
时,y=﹣3.下面是小童探究的过程,请补充完整:
(1)该函数的解析式为 ,m= ,n= .
根据图中描出的点,画出函数图象.
x | … | ﹣4 | ﹣3 | ﹣2 | 0 | 2 | 3 | 4 | … |
y | … | m |  |  | ﹣3 | 7 | n |  | … |
①该函数图象是中心对称图形,它的对称中心是原点.
②该函数既无最大值也无最小值.
③在自变量的取值范围内,y随x的增大而减小.
(3)请结合(1)中函数图象,直接写出关于x的不等式
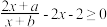 的解集.(保留1位小数,误差不超过0.2)
的解集.(保留1位小数,误差不超过0.2)
您最近一年使用:0次
2022-02-25更新
|
237次组卷
|
3卷引用:2021年重庆市北碚区西南大学附中中考数学四模试题