1 . 通常我们把一个以集合作为元素的集合称为族.若以集合 的子集为元素的族
的子集为元素的族 ,满足下列三个条件:(1)
,满足下列三个条件:(1) 和
和 在
在 中;(2)
中;(2) 中的有限个元素取交后得到的集合在
中的有限个元素取交后得到的集合在 中;(3)
中;(3) 中的任意多个元素取并后得到的集合在
中的任意多个元素取并后得到的集合在 中,则称族
中,则称族 为集合
为集合 上的一个拓扑.已知全集
上的一个拓扑.已知全集 为
为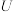 的非空真子集,且
的非空真子集,且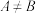 ,则( )
,则( )
 的子集为元素的族
的子集为元素的族 ,满足下列三个条件:(1)
,满足下列三个条件:(1) 和
和 在
在 中;(2)
中;(2) 中的有限个元素取交后得到的集合在
中的有限个元素取交后得到的集合在 中;(3)
中;(3) 中的任意多个元素取并后得到的集合在
中的任意多个元素取并后得到的集合在 中,则称族
中,则称族 为集合
为集合 上的一个拓扑.已知全集
上的一个拓扑.已知全集 为
为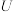 的非空真子集,且
的非空真子集,且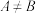 ,则( )
,则( )A.族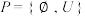 为集合 为集合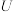 上的一个拓扑 上的一个拓扑 |
B.族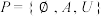 为集合 为集合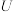 上的一个拓扑 上的一个拓扑 |
C.族 为集合 为集合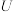 上的一个拓扑 上的一个拓扑 |
D.若族 为集合 为集合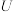 上的一个拓扑,将 上的一个拓扑,将 的每个元素的补集放在一起构成族 的每个元素的补集放在一起构成族 ,则 ,则 也是集合 也是集合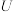 上的一个拓扑 上的一个拓扑 |
您最近一年使用:0次
名校
2 . 已知集合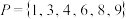 ,对于它的任一非空子集
,对于它的任一非空子集 ,可以将
,可以将 中的每一个元素
中的每一个元素 都乘
都乘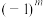 再求和,例如
再求和,例如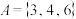 ,则可求得和为
,则可求得和为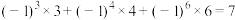 ,对
,对 所有非空子集,这些和的总和为( )
所有非空子集,这些和的总和为( )
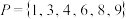 ,对于它的任一非空子集
,对于它的任一非空子集 ,可以将
,可以将 中的每一个元素
中的每一个元素 都乘
都乘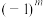 再求和,例如
再求和,例如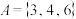 ,则可求得和为
,则可求得和为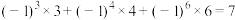 ,对
,对 所有非空子集,这些和的总和为( )
所有非空子集,这些和的总和为( )A. | B. | C. | D. |
您最近一年使用:0次
2022-11-18更新
|
596次组卷
|
10卷引用:山东省淄博市淄博实验中学2022-2023学年高一上学期期末数学试题
山东省淄博市淄博实验中学2022-2023学年高一上学期期末数学试题湖南省三湘名校教育联盟2022-2023学年高一上学期期中联考数学试题河南省部分学校2022-2023学年高一上学期11月联考数学试题广东省湛江市四校2022-2023学年高一上学期第二次联考数学试题青海省西宁市青海湟川中学2022-2023学年高一上学期12月学情调研测试数学试题青海省青海湟川中学2022-2023学年高一上学期12月月考数学试题江苏省连云港市灌南高级中学2022-2023学年高一提优班上学期11月解题能力大赛数学试题(已下线)第03讲 1.3集合的基本运算(1)-【帮课堂】(已下线)重难点02 集合中的创新问题(1)-【帮课堂】高一数学同步学与练(苏教版2019必修第一册)(已下线)第一章 集合与常用逻辑用语(知识归纳+7类题型突破)-速记·巧练(人教A版2019必修第一册)
3 . 非空集合 关于运算
关于运算 满足:对于任意的
满足:对于任意的 、
、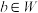 ,都有
,都有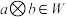 ,则称集合
,则称集合 关于运算
关于运算 为“回归集”.下列集合
为“回归集”.下列集合 关于运算
关于运算 为“回归集”的是( )
为“回归集”的是( )
 关于运算
关于运算 满足:对于任意的
满足:对于任意的 、
、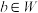 ,都有
,都有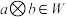 ,则称集合
,则称集合 关于运算
关于运算 为“回归集”.下列集合
为“回归集”.下列集合 关于运算
关于运算 为“回归集”的是( )
为“回归集”的是( )A. 为 为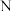 , , 为自然数的减法 为自然数的减法 |
B. 为 为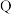 , , 为有理数的乘法 为有理数的乘法 |
C. 为 为 , , 为实数的加法 为实数的加法 |
D.已知全集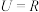 ,集合 ,集合 , , 为 为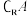 , , 为实数的乘法 为实数的乘法 |
您最近一年使用:0次
2022-07-07更新
|
1291次组卷
|
6卷引用:山东省青岛市2021-2022学年高二下学期期末数学试题
山东省青岛市2021-2022学年高二下学期期末数学试题第一章 集合与常用逻辑用语(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第一册)(已下线)第一章 集合与常用逻辑用语知识(2)(已下线)第一篇 代数与近世代数 专题2 群、环、域等新定义问题 微点2 群、环、域等新定义问题综合训练加习题(已下线)第03讲 1.3集合的基本运算(2)-【帮课堂】(已下线)第03讲 集合与常用逻辑用语章节综合测试(能力提升卷)-【练透核心考点】
4 . 定义集合运算: .若集合
.若集合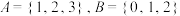 ,则
,则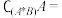 ( )
( )
 .若集合
.若集合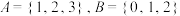 ,则
,则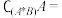 ( )
( )A. | B.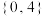 | C.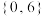 | D. |
您最近一年使用:0次
2022-01-23更新
|
1125次组卷
|
7卷引用:山东省青岛市四区2021-2022学年高三上学期期末考试数学试题
山东省青岛市四区2021-2022学年高三上学期期末考试数学试题山东省青岛市4区县2021-2022学年高三上学期期末考试数学试题(已下线)知识点 集合的基本运算 易错点2 背景理解有误(已下线)第1章 集合(培优卷)安徽省滁州市定远县育才学校2021-2022学年高一上学期期末考试数学试题天津市复兴中学2021-2022学年高三上学期第二次月考数学试题(已下线)艺体生一轮复习 第二章 集合、常用逻辑用语与不等式 第5讲 集合【练】



