名校
1 . 在计算机科学中, 维数组
维数组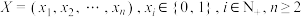 是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于
是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于 维数组
维数组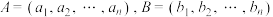 ,定义
,定义 与
与 的差为
的差为 与
与 之间的距离为
之间的距离为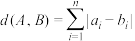 .
.
(1)若 维数组
维数组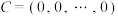 ,证明:
,证明: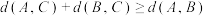 ;
;
(2)证明:对任意的数组 ,有
,有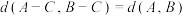 ;
;
(3)设集合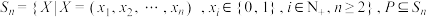 ,若集合
,若集合 中有
中有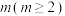 个
个 维数组,记
维数组,记 中所有两元素间的距离的平均值为
中所有两元素间的距离的平均值为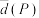 ,证明:
,证明: .
.
 维数组
维数组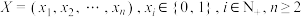 是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于
是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于 维数组
维数组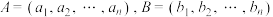 ,定义
,定义 与
与 的差为
的差为 与
与 之间的距离为
之间的距离为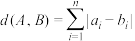 .
.(1)若
 维数组
维数组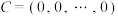 ,证明:
,证明: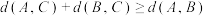 ;
;(2)证明:对任意的数组
 ,有
,有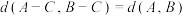 ;
;(3)设集合
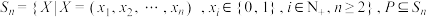 ,若集合
,若集合 中有
中有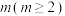 个
个 维数组,记
维数组,记 中所有两元素间的距离的平均值为
中所有两元素间的距离的平均值为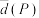 ,证明:
,证明: .
.
您最近半年使用:0次
名校
2 . 设非空数集M,对于M中的任意两个元素,如果满足:①两个元素之和属于M ②两个元素之差属于M.③两个元素之积属于M ④两个元素之商(分母不为零)也属于M.定义:满足条件①②③的数集M为数环(即数环对于加、减、乘运算封闭);满足④的数环M为数域(即数域对于加、减、乘、除运算封闭).
(1)判断自然数集N、整数集Z、有理数集Q、实数集R、复数集C是不是数环,假如该集合是数环,那么它是不是数域(无需说明理由);
(2)若M是一个数环,证明: ;若S是一个数域,证明:
;若S是一个数域,证明: ;
;
(3)设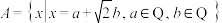 ,证明A是数域.
,证明A是数域.
(1)判断自然数集N、整数集Z、有理数集Q、实数集R、复数集C是不是数环,假如该集合是数环,那么它是不是数域(无需说明理由);
(2)若M是一个数环,证明:
 ;若S是一个数域,证明:
;若S是一个数域,证明: ;
;(3)设
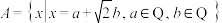 ,证明A是数域.
,证明A是数域.
您最近半年使用:0次
3 . 已知点集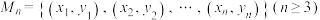 满足
满足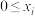 ,
, ,
,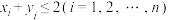 .对于任意点集
.对于任意点集 ,若其非空子集A,B满足
,若其非空子集A,B满足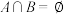 ,
, ,则称集合对
,则称集合对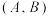 为
为 的一个优划分.对任意点集
的一个优划分.对任意点集 及其优划分
及其优划分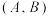 ,记A中所有点的横坐标之和为
,记A中所有点的横坐标之和为 ,B中所有点的纵坐标之和为
,B中所有点的纵坐标之和为 .
.
(1)写出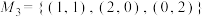 的一个优划分
的一个优划分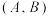 ,使其满足
,使其满足 ;
;
(2)对于任意点集 ,求证:存在
,求证:存在 的一个优划分
的一个优划分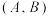 ,满足
,满足 ;
;
(3)对于任意点集 ,求证:存在
,求证:存在 的一个优划分
的一个优划分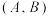 ,满足
,满足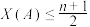 且
且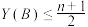 .
.
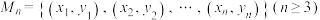 满足
满足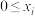 ,
, ,
,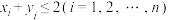 .对于任意点集
.对于任意点集 ,若其非空子集A,B满足
,若其非空子集A,B满足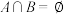 ,
, ,则称集合对
,则称集合对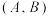 为
为 的一个优划分.对任意点集
的一个优划分.对任意点集 及其优划分
及其优划分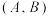 ,记A中所有点的横坐标之和为
,记A中所有点的横坐标之和为 ,B中所有点的纵坐标之和为
,B中所有点的纵坐标之和为 .
.(1)写出
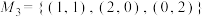 的一个优划分
的一个优划分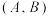 ,使其满足
,使其满足 ;
;(2)对于任意点集
 ,求证:存在
,求证:存在 的一个优划分
的一个优划分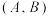 ,满足
,满足 ;
;(3)对于任意点集
 ,求证:存在
,求证:存在 的一个优划分
的一个优划分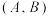 ,满足
,满足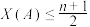 且
且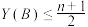 .
.
您最近半年使用:0次
4 . 设A,B是两个非空集合,如果对于集合A中的任意一个元素x,按照某种确定的对应关系 ,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称
,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称 :
: 为从集合A到集合B的一一对应,并称集合A与B等势,记作
为从集合A到集合B的一一对应,并称集合A与B等势,记作 .若集合A与B之间不存在一一对应关系,则称A与B不等势,记作
.若集合A与B之间不存在一一对应关系,则称A与B不等势,记作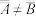 .
.
例如:对于集合 ,
, ,存在一一对应关系
,存在一一对应关系 ,因此
,因此 .
.
(1)已知集合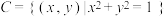 ,
,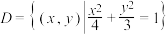 ,试判断
,试判断 是否成立?请说明理由;
是否成立?请说明理由;
(2)证明:① ;
;
② .
.
 ,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称
,在集合B中都有唯一确定的元素y和它对应,并且不同的x对应不同的y;同时B中的每一个元素y,都有一个A中的元素x与它对应,则称 :
: 为从集合A到集合B的一一对应,并称集合A与B等势,记作
为从集合A到集合B的一一对应,并称集合A与B等势,记作 .若集合A与B之间不存在一一对应关系,则称A与B不等势,记作
.若集合A与B之间不存在一一对应关系,则称A与B不等势,记作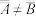 .
.例如:对于集合
 ,
, ,存在一一对应关系
,存在一一对应关系 ,因此
,因此 .
.(1)已知集合
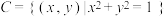 ,
,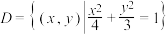 ,试判断
,试判断 是否成立?请说明理由;
是否成立?请说明理由;(2)证明:①
 ;
;②
 .
.
您最近半年使用:0次
5 . 如果一个非空集合 上定义了一个运算
上定义了一个运算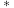 ,满足如下性质,则称
,满足如下性质,则称 关于运算
关于运算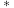 构成一个群.
构成一个群.
(1) 封闭性,即对于任意的 ,有
,有 ;
;
(2) 结合律,即对于任意的 ,有
,有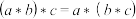 ;
;
(3) 对于任意的 ,方程
,方程 与
与 在
在 中都有解.
中都有解.
例如,整数集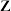 关于整数的加法(
关于整数的加法( )构成群,因为任意两个整数的和还是整数,且满足加法结合律,对于任意的
)构成群,因为任意两个整数的和还是整数,且满足加法结合律,对于任意的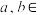
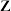 ,方程
,方程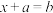 与
与 都有整数解;而实数集
都有整数解;而实数集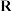 关于实数的乘法(
关于实数的乘法( )不构成群,因为方程
)不构成群,因为方程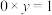 没有实数解.
没有实数解.
以下关于“群”的真命题有( )
①自然数集 关于自然数的加法(
关于自然数的加法( )构成群;
)构成群;
②有理数集 关于有理数的乘法(
关于有理数的乘法( )构成群;
)构成群;
③平面向量集关于向量的数量积( )构成群;
)构成群;
④复数集 关于复数的加法(
关于复数的加法( )构成群.
)构成群.
 上定义了一个运算
上定义了一个运算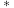 ,满足如下性质,则称
,满足如下性质,则称 关于运算
关于运算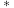 构成一个群.
构成一个群.(1) 封闭性,即对于任意的
 ,有
,有 ;
;(2) 结合律,即对于任意的
 ,有
,有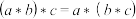 ;
;(3) 对于任意的
 ,方程
,方程 与
与 在
在 中都有解.
中都有解.例如,整数集
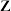 关于整数的加法(
关于整数的加法( )构成群,因为任意两个整数的和还是整数,且满足加法结合律,对于任意的
)构成群,因为任意两个整数的和还是整数,且满足加法结合律,对于任意的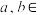
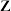 ,方程
,方程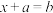 与
与 都有整数解;而实数集
都有整数解;而实数集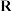 关于实数的乘法(
关于实数的乘法( )不构成群,因为方程
)不构成群,因为方程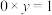 没有实数解.
没有实数解.以下关于“群”的真命题有( )
①自然数集
 关于自然数的加法(
关于自然数的加法( )构成群;
)构成群;②有理数集
 关于有理数的乘法(
关于有理数的乘法( )构成群;
)构成群;③平面向量集关于向量的数量积(
 )构成群;
)构成群;④复数集
 关于复数的加法(
关于复数的加法( )构成群.
)构成群.| A.0个; | B.1个; | C.2个; | D.3个. |
您最近半年使用:0次
6 . 指示函数是一个重要的数学函数,通常用来表示某个条件的成立情况.已知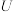 为全集且元素个数有限,对于
为全集且元素个数有限,对于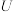 的任意一个子集
的任意一个子集 ,定义集合
,定义集合 的指示函数
的指示函数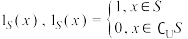 若
若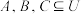 ,则( )
,则( )
注: 表示
表示 中所有元素
中所有元素 所对应的函数值
所对应的函数值 之和(其中
之和(其中 是
是 定义域的子集).
定义域的子集).
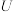 为全集且元素个数有限,对于
为全集且元素个数有限,对于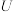 的任意一个子集
的任意一个子集 ,定义集合
,定义集合 的指示函数
的指示函数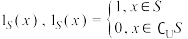 若
若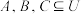 ,则( )
,则( )注:
 表示
表示 中所有元素
中所有元素 所对应的函数值
所对应的函数值 之和(其中
之和(其中 是
是 定义域的子集).
定义域的子集).A.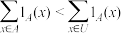 |
B. |
C.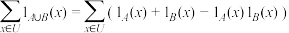 |
D.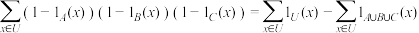 |
您最近半年使用:0次
7 . 已知 ,集合
,集合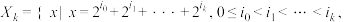 其中
其中 .
.
(1)求 中最小的元素;
中最小的元素;
(2)设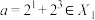 ,
,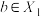 ,且
,且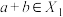 ,求
,求 的值;
的值;
(3)记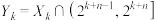 ,
,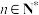 ,若集合
,若集合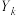 中的元素个数为
中的元素个数为 ,求
,求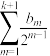 .
.
 ,集合
,集合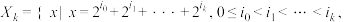 其中
其中 .
.(1)求
 中最小的元素;
中最小的元素;(2)设
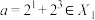 ,
,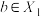 ,且
,且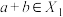 ,求
,求 的值;
的值;(3)记
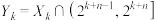 ,
,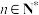 ,若集合
,若集合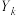 中的元素个数为
中的元素个数为 ,求
,求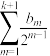 .
.
您最近半年使用:0次
2024·全国·模拟预测
解题方法
8 . 在平面直角坐标系中,两点 的“曼哈顿距离”定义为
的“曼哈顿距离”定义为 ,记为
,记为 ,如点
,如点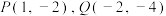 的“曼哈顿距离”为5,记为
的“曼哈顿距离”为5,记为
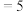 .
.
(1)若点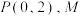 是满足
是满足
 的动点
的动点 的集合,求点集
的集合,求点集 所占区域的面积;
所占区域的面积;
(2)若动点 在直线
在直线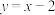 上,动点
上,动点 在函数
在函数 的图象上,求
的图象上,求 的最小值;
的最小值;
(3)设点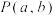 ,动点
,动点 在函数
在函数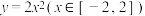 的图象上,
的图象上, 的最大值记为
的最大值记为 ,求
,求 的最小值.
的最小值.
 的“曼哈顿距离”定义为
的“曼哈顿距离”定义为 ,记为
,记为 ,如点
,如点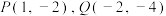 的“曼哈顿距离”为5,记为
的“曼哈顿距离”为5,记为
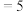 .
.(1)若点
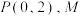 是满足
是满足
 的动点
的动点 的集合,求点集
的集合,求点集 所占区域的面积;
所占区域的面积;(2)若动点
 在直线
在直线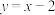 上,动点
上,动点 在函数
在函数 的图象上,求
的图象上,求 的最小值;
的最小值;(3)设点
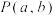 ,动点
,动点 在函数
在函数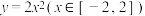 的图象上,
的图象上, 的最大值记为
的最大值记为 ,求
,求 的最小值.
的最小值.
您最近半年使用:0次
9 . 已知数列 的各项均为正整数,设集合
的各项均为正整数,设集合 ,
,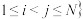 ,记
,记 的元素个数为
的元素个数为 .
.
(1)若数列A:1,3,5,7,求集合 ,并写出
,并写出 的值;
的值;
(2)若 是递减数列,求证:“
是递减数列,求证:“ ”的充要条件是“
”的充要条件是“ 为等差数列”;
为等差数列”;
(3)已知数列 ,求证:
,求证: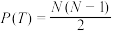 .
.
 的各项均为正整数,设集合
的各项均为正整数,设集合 ,
,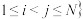 ,记
,记 的元素个数为
的元素个数为 .
.(1)若数列A:1,3,5,7,求集合
 ,并写出
,并写出 的值;
的值;(2)若
 是递减数列,求证:“
是递减数列,求证:“ ”的充要条件是“
”的充要条件是“ 为等差数列”;
为等差数列”;(3)已知数列
 ,求证:
,求证: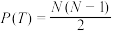 .
.
您最近半年使用:0次
10 . 设A,B为两个非空有限集合,定义 其中
其中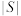 表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为
表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为 ,
, ,
, ,
,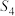 .已知
.已知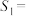 {物理,化学,生物},
{物理,化学,生物},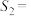 {地理,物理,化学},
{地理,物理,化学}, {思想政治,历史,地理},给出下列四个结论:
{思想政治,历史,地理},给出下列四个结论:
①若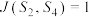 ,则
,则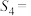 {思想政治,历史,生物};
{思想政治,历史,生物};
②若 ,则
,则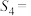 {地理,物理,化学};
{地理,物理,化学};
③若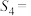 {思想政治,物理,生物},则
{思想政治,物理,生物},则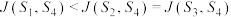 ;
;
④若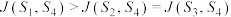 ,则
,则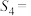 {思想政治,地理,化学}.
{思想政治,地理,化学}.
其中所有正确结论的序号是__________ .
 其中
其中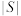 表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为
表示集合S的元素个数.某学校甲、乙、丙、丁四名同学从思想政治、历史、地理、物理、化学、生物这6门高中学业水平等级性考试科目中自主选择3门参加考试,设这四名同学的选考科目组成的集合分别为 ,
, ,
, ,
,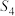 .已知
.已知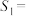 {物理,化学,生物},
{物理,化学,生物},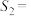 {地理,物理,化学},
{地理,物理,化学}, {思想政治,历史,地理},给出下列四个结论:
{思想政治,历史,地理},给出下列四个结论:①若
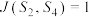 ,则
,则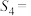 {思想政治,历史,生物};
{思想政治,历史,生物};②若
 ,则
,则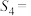 {地理,物理,化学};
{地理,物理,化学};③若
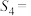 {思想政治,物理,生物},则
{思想政治,物理,生物},则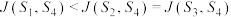 ;
;④若
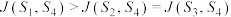 ,则
,则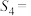 {思想政治,地理,化学}.
{思想政治,地理,化学}.其中所有正确结论的序号是
您最近半年使用:0次



