名校
1 . 用铁皮围成一个容积为 的无盖正四棱柱形水箱,需用铁皮的面积至少为
的无盖正四棱柱形水箱,需用铁皮的面积至少为_____ 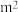 .(注:铁皮厚度不计,接缝处损耗不计)
.(注:铁皮厚度不计,接缝处损耗不计)
 的无盖正四棱柱形水箱,需用铁皮的面积至少为
的无盖正四棱柱形水箱,需用铁皮的面积至少为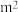 .(注:铁皮厚度不计,接缝处损耗不计)
.(注:铁皮厚度不计,接缝处损耗不计)
您最近一年使用:0次
2021-08-06更新
|
458次组卷
|
3卷引用:北京市西城区2020-2021学年高二下学期期末数学试题
解题方法
2 . 易拉罐用料最省问题的研究.小明同学最近注意到一条新闻,易拉罐(如图所示)作为饮品的容器,每年的用量可达数万亿个.这让他想到一个用料最优化的问题,即在易拉罐的体积一定的情况下,如何确定易拉罐的高和半径才能使得用料最省?他研究发现易拉罐的上盖、下底和侧壁的厚度是不同的,进而结合数学建模知识进行了深入研究.以下是小明的研究过程,请你补全缺失的部分.

以下是小明的研究过程,请你补全缺失的部分.
(1)模型假设:
①易拉罐近似看成圆柱体;
②上盖、下底、侧壁的厚度处处均匀;
③上盖、下底、侧壁所用金属相同;
④易拉罐接口处的所用材料忽略不计.
(2)建立模型
记圆柱体积为 ,高为
,高为 ,底面半径为
,底面半径为 ,上盖、下底和侧壁的厚度分别为
,上盖、下底和侧壁的厚度分别为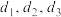 ,
,
金属用料总量为C.
由几何知识得到如下数量关系:
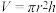 ①
①
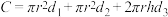 ②
②
因为 都是常数,不妨设
都是常数,不妨设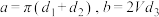 ,
,
则用料总量的函数简化为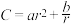 .
.
请写出表格中代入整理这一步的目的是:___________________________.
(3)求解模型:
所以,在 ___________(用
___________(用 表示)时,
表示)时, 取得最小值,即在此种情况下用料最省.
取得最小值,即在此种情况下用料最省.
(4)检验模型:
小明上网查阅到目前330毫升可乐易拉罐的数据,得知
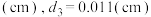 ,代入(3)的模型结果,经计算得
,代入(3)的模型结果,经计算得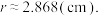 经验算,确认计算无误,但是这与实际罐体半径
经验算,确认计算无误,但是这与实际罐体半径 差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优.
差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优.
(5)模型评价与改进:
模型计算结果与现实数据存在较大差异的原因可能为:_________________________________________________________________________________________________.
相应改进措施为:_________________________________________________________________________________________________________________________________.

以下是小明的研究过程,请你补全缺失的部分.
(1)模型假设:
①易拉罐近似看成圆柱体;
②上盖、下底、侧壁的厚度处处均匀;
③上盖、下底、侧壁所用金属相同;
④易拉罐接口处的所用材料忽略不计.
(2)建立模型
记圆柱体积为
 ,高为
,高为 ,底面半径为
,底面半径为 ,上盖、下底和侧壁的厚度分别为
,上盖、下底和侧壁的厚度分别为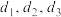 ,
,金属用料总量为C.
由几何知识得到如下数量关系:
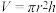 ①
①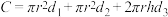 ②
②由①得 ,代入②整理得: ,代入②整理得: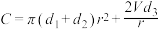 . . |
 都是常数,不妨设
都是常数,不妨设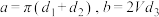 ,
,则用料总量的函数简化为
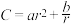 .
.请写出表格中代入整理这一步的目的是:___________________________.
(3)求解模型:
所以,在
 ___________(用
___________(用 表示)时,
表示)时, 取得最小值,即在此种情况下用料最省.
取得最小值,即在此种情况下用料最省.(4)检验模型:
小明上网查阅到目前330毫升可乐易拉罐的数据,得知

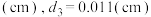 ,代入(3)的模型结果,经计算得
,代入(3)的模型结果,经计算得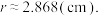 经验算,确认计算无误,但是这与实际罐体半径
经验算,确认计算无误,但是这与实际罐体半径 差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优.
差异较大.实际上,在经济利益驱动之下,目前的罐体成本应该已经达最优.(5)模型评价与改进:
模型计算结果与现实数据存在较大差异的原因可能为:_________________________________________________________________________________________________.
相应改进措施为:_________________________________________________________________________________________________________________________________.
您最近一年使用:0次
解题方法
3 . 某景区准备设计一景观,其上部是圆锥形的顶棚,如图所示.圆锥顶点为B,底面圆心为O,半径为2米.通过金属杆AB支撑在地面A处(AB垂直于地面),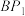 ,
,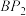 ,…,
,…, 支撑着顶棚,
支撑着顶棚, ,
, ,
,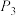 ,…,
,…, 是底面圆周上的n等分点,圆锥顶点距地面10米,设金属杆
是底面圆周上的n等分点,圆锥顶点距地面10米,设金属杆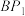 ,
,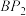 ,…,
,…, 所在直线与圆锥底面所成的角都为
所在直线与圆锥底面所成的角都为 (金属杆不计粗细).
(金属杆不计粗细).
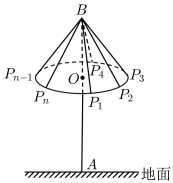
(1)当 为60°且n=3时,求AO,
为60°且n=3时,求AO,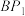 ,
,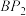 ,
,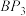 的总长.
的总长.
(2)当n一定, 变化时,为美观与安全起见,要求AO,
变化时,为美观与安全起见,要求AO,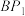 ,
,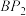 ,…,
,…, 的总长最短,此时
的总长最短,此时 的正弦值是多少?并由此说明n越大,O点的位置将会上移还是下移.
的正弦值是多少?并由此说明n越大,O点的位置将会上移还是下移.
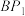 ,
,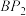 ,…,
,…, 支撑着顶棚,
支撑着顶棚, ,
, ,
,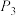 ,…,
,…, 是底面圆周上的n等分点,圆锥顶点距地面10米,设金属杆
是底面圆周上的n等分点,圆锥顶点距地面10米,设金属杆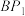 ,
,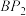 ,…,
,…, 所在直线与圆锥底面所成的角都为
所在直线与圆锥底面所成的角都为 (金属杆不计粗细).
(金属杆不计粗细).
(1)当
 为60°且n=3时,求AO,
为60°且n=3时,求AO,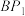 ,
,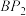 ,
,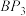 的总长.
的总长.(2)当n一定,
 变化时,为美观与安全起见,要求AO,
变化时,为美观与安全起见,要求AO,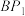 ,
,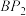 ,…,
,…, 的总长最短,此时
的总长最短,此时 的正弦值是多少?并由此说明n越大,O点的位置将会上移还是下移.
的正弦值是多少?并由此说明n越大,O点的位置将会上移还是下移.
您最近一年使用:0次



