1 . 类比思想在数学中极为重要，例如类比于二维平面内的余弦定理，有三维空间中的三面角余弦定理，如图1，由射线PA，PB，PC构成的三面角P-ABC，记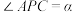
，
，
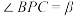，二面角A-PC-B的大小为
，则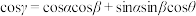
．
如图2，四棱柱
中，底面ABCD为菱形，
，
，
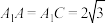，且
．
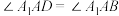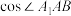的值；
(2)在图2中，直线
与平面ABCD内任意一条直线的夹角为φ，证明：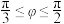
；
(3)在图2中，过点B作平面
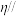，使平面
平面
，且与直线
相交于点P，求
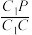的值．
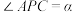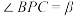，，，二面角A-PC-B的大小为，则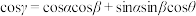．如图2，四棱柱
中，底面ABCD为菱形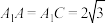，，，，且．
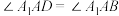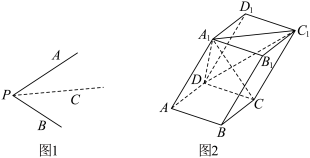
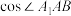的值；(2)在图2中，直线
与平面ABCD内任意一条直线的夹角为φ，证明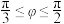：；(3)在图2中，过点B作平面
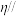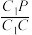，使平面平面，且与直线相交于点P，求的值．
您最近一年使用：0次
2024-09-03更新
|
317次组卷
|
2卷引用：湖北省鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高二上学期起点考试数学试卷
