1 . 类比思想在数学中极为重要,例如类比于二维平面内的余弦定理,有三维空间中的三面角余弦定理:如图1,由射线 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记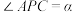 ,
,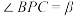 ,
, ,二面角
,二面角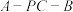 的大小为
的大小为 ,则
,则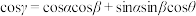 .如图2,四棱柱
.如图2,四棱柱 中,
中,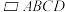 为菱形,
为菱形, ,
,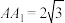 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.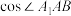 的值;
的值;
(2)直线 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: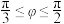 ;
;
(3)过点 作平面
作平面 ,使平面
,使平面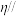 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
 ,
, ,
, 构成的三面角
构成的三面角 ,记
,记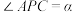 ,
,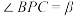 ,
, ,二面角
,二面角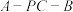 的大小为
的大小为 ,则
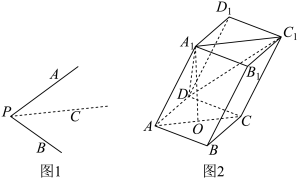
,则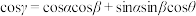 .如图2,四棱柱
.如图2,四棱柱 中,
中,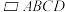 为菱形,
为菱形, ,
,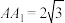 ,
, ,且
,且 点在底面
点在底面 内的射影为
内的射影为 的中点
的中点 .
.
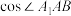 的值;
的值;(2)直线
 与平面
与平面 内任意一条直线夹角为
内任意一条直线夹角为 ,证明:
,证明: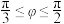 ;
;(3)过点
 作平面
作平面 ,使平面
,使平面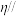 平面
平面 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 ,求
,求 值.
值.
您最近一年使用:0次
2024-07-20更新
|
782次组卷
|
6卷引用:湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题
湖北省黄冈市浠水县第一中学2024-2025学年高二上学期9月月考数学试题山东省德州市夏津育中万隆中英文高级中学2024-2025学年高二上学期第一次月考数学试题河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题山东省临沂市2023-2024学年高一下学期期末学科素养水平监测数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2(已下线)拔高点突破04 新情景、新定义下的立体几何问题(六大题型)-1
2 . 四面体 中,
中,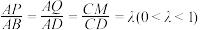 ,平面
,平面 交
交 于点
于点 ,则下列结论正确的是( )
,则下列结论正确的是( )
 中,
中,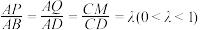 ,平面
,平面 交
交 于点
于点 ,则下列结论正确的是( )
,则下列结论正确的是( )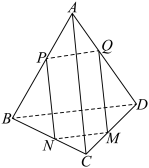
A.四边形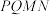 可以不是平行四边形 可以不是平行四边形 |
B.四边形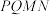 是矩形的充要条件是 是矩形的充要条件是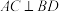 |
C.当 时,四边形 时,四边形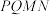 的面积最大 的面积最大 |
D.当 时,截面 时,截面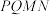 刚好平分四面体 刚好平分四面体 的体积 的体积 |
您最近一年使用:0次
名校
解题方法
3 . 如图,正三棱锥 和正三棱锥
和正三棱锥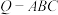 的侧棱长分别为2,
的侧棱长分别为2, ,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
 和正三棱锥
和正三棱锥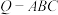 的侧棱长分别为2,
的侧棱长分别为2, ,直线PQ与底面ABC相交于点O,OP=2OQ,则( )
,直线PQ与底面ABC相交于点O,OP=2OQ,则( )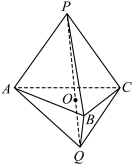
A.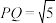 |
| B.AQ,BQ,CQ两两垂直 |
| C.AP与CQ的夹角为45° |
| D.点P,A,B,C,Q不可能同时在某个球的表面上 |
您最近一年使用:0次
2023-06-22更新
|
556次组卷
|
8卷引用:湖北省恩施州巴东县第三高级中学2023-2024学年高二上学期第二次月考数学试题
名校
解题方法
4 . 已知 ,
, 为两条异面直线,在直线
为两条异面直线,在直线 上取点
上取点 ,
, ,在直线
,在直线 上取点
上取点 ,
, ,使
,使 ,且
,且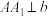 (称
(称 为异面直线
为异面直线 ,
, 的公垂线).已知
的公垂线).已知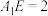 ,
,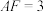 ,
, ,
, ,则异面直线
,则异面直线 ,
, 所成的角为( )
所成的角为( )
 ,
, 为两条异面直线,在直线
为两条异面直线,在直线 上取点
上取点 ,
, ,在直线
,在直线 上取点
上取点 ,
, ,使
,使 ,且
,且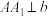 (称
(称 为异面直线
为异面直线 ,
, 的公垂线).已知
的公垂线).已知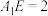 ,
,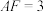 ,
, ,
, ,则异面直线
,则异面直线 ,
, 所成的角为( )
所成的角为( )A.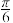 | B. | C.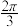 | D. |
您最近一年使用:0次
2021-10-14更新
|
558次组卷
|
6卷引用:湖北省潜江市园林高级中学2022-2023学年高二上学期10月月考数学试题
湖北省潜江市园林高级中学2022-2023学年高二上学期10月月考数学试题山西省运城市教育发展联盟2021-2022学年高二上学期10月月考数学试题山东省青岛市4区市2021-2022学年高二上学期期中考试数学试题山西省平遥中学校2021-2022学年高二上学期期中数学试题山东省泰安市2022-2023学年高二上学期期中考试数学试题(已下线)第二章 立体几何中的计算 专题二 空间距离 微点8 空间两条直线的距离(四)【培优版】



