名校
1 . (1)化简: .
.
(2)求证: .
.
 .
.(2)求证:
 .
.
您最近一年使用:0次
名校
解题方法
2 . 已知函数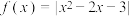 .
.
(1)求不等式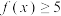 的解集;
的解集;
(2)设函数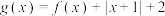 的最小值为
的最小值为 ,若
,若 且
且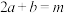 ,求证:
,求证: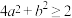 .
.
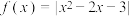 .
.(1)求不等式
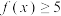 的解集;
的解集;(2)设函数
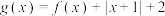 的最小值为
的最小值为 ,若
,若 且
且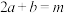 ,求证:
,求证: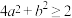 .
.
您最近一年使用:0次
2024-02-05更新
|
936次组卷
|
8卷引用:四川省内江市威远中学校2024届高三下期第一次月考理科数学试题
名校
解题方法
3 . 已知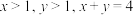 .
.
(1)求证: ;
;
(2)求 的最小值.
的最小值.
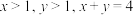 .
.(1)求证:
 ;
;(2)求
 的最小值.
的最小值.
您最近一年使用:0次
2023-08-15更新
|
1742次组卷
|
7卷引用:四川省内江市第六中学2023-2024学年高一上学期入学考试(精英班)数学试题
四川省内江市第六中学2023-2024学年高一上学期入学考试(精英班)数学试题陕西省渭南市韩城市新蕾中学2020-2021学年高二上学期第二次月考检测理科数学试题(已下线)3.2基本不等式-高一数学同步精品课堂(北师大版2019必修第一册)(已下线)第3章 不等式 章末题型归纳总结(1)-【帮课堂】(苏教版2019必修第一册)广西南宁第三中学2023-2024学年高一上学期第一次月考前数学模拟试题(1)福建省福州市闽侯县第一中学2023-2024学年高一上学期第一次月考(10月)数学试题甘肃省庆阳市环县第一中学2023-2024学年高一上学期第一次月考数学试题
名校
解题方法
4 . 已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若对任意的
,若对任意的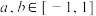 且
且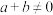 时,有
时,有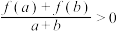 成立.
成立.
(1)证明: 在
在 上单调递增;
上单调递增;
(2)解不等式: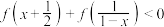 ;
;
(3)若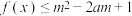 对所有的
对所有的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若对任意的
,若对任意的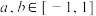 且
且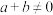 时,有
时,有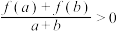 成立.
成立.(1)证明:
 在
在 上单调递增;
上单调递增;(2)解不等式:
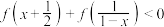 ;
;(3)若
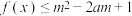 对所有的
对所有的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
5 . 已知函数 对于任意
对于任意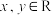 ,总有
,总有 ,且
,且 时,
时,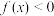 .
.
(1)求证: 在
在 上是奇函数;
上是奇函数;
(2)求证: 在
在 上是减函数;
上是减函数;
(3)若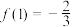 ,求
,求 在区间
在区间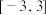 上的最大值和最小值.
上的最大值和最小值.
 对于任意
对于任意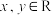 ,总有
,总有 ,且
,且 时,
时,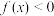 .
.(1)求证:
 在
在 上是奇函数;
上是奇函数;(2)求证:
 在
在 上是减函数;
上是减函数;(3)若
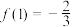 ,求
,求 在区间
在区间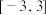 上的最大值和最小值.
上的最大值和最小值.
您最近一年使用:0次
2023-07-05更新
|
2253次组卷
|
10卷引用:四川省内江市威远县威远中学校2022-2023学年高一上学期期中数学试题
四川省内江市威远县威远中学校2022-2023学年高一上学期期中数学试题新疆兵团第二师华山中学2018-2019学年高一上学期第一次调研考试数学试题(已下线)考点08 函数的单调性与最值(考点专练)-备战2021年新高考数学一轮复习考点微专题湖南师范大学附属中学2020-2021学年高一上学期期中数学试题广东省江门市台山广旭实验学校2022-2023学年高一上学期期中数学试题(已下线)第二章 函数的概念与性质 第二节 函数的单调性与最值(讲)(已下线)专题3.5 函数性质及其应用大题专项训练【六大题型】-举一反三系列(已下线)专题3.2 函数的基本性质【十大题型】-举一反三系列(已下线)考点05 函数的奇偶性 2024届高考数学考点总动员【练】甘肃省兰州市第六十一中学(兰化一中)2024届高三上学期期中考试数学试题
名校
解题方法
6 . 已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求 ,
, 的值;
的值;
(2)用定义法证明函数 在
在 上单调递增;
上单调递增;
(3)若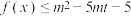 对于任意的
对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.(1)求
 ,
, 的值;
的值;(2)用定义法证明函数
 在
在 上单调递增;
上单调递增;(3)若
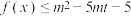 对于任意的
对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-08-17更新
|
2698次组卷
|
20卷引用:四川省内江市第二中学2023-2024学年高一上学期期中考试数学试题
四川省内江市第二中学2023-2024学年高一上学期期中考试数学试题四川省南充市第一中学2022-2023学年高一上学期11月月考数学试题黑龙江省鸡西实验中学2023-2024学年高三上学期第一次考试数学试题(已下线)高一上学期期中考试解答题压轴题50题专练-举一反三系列吉林省长春汽车经济技术开发区第三中学2023-2024学年高一上学期10月月考数学试题云南省下关第一中学2023-2024学年高一上学期10月月考数学试题湖北省荆州市沙市中学2023-2024学年高一上学期10月月考数学试题(已下线)专题02 高一上期中真题精选-期中考点大串讲(人教A版2019必修第一册)广东省中山市龙山中学2023-2024学年高一上学期10月月考数学试题广东省广州市第六十五中学2023-2024学年高一上学期期中数学试题(已下线)高一数学上学期期中考试模拟卷山东省淄博第七中学2023-2024学年高一上学期期中考试数学试题四川省成都市第二十中学校2023-2024学年高一上学期期中数学试题广东省江门市第一中学2023-2024学年高一上学期第二次段考数学试题(已下线)必修第一册综合检测(基础)-【优化数学】单元测试基础卷(人教A版2019)广东省江门市第一中学2023-2024学年高一下学期启超班期中数学试题(已下线)专题3 函数性质的综合应用【讲】(高一期中压轴专项)解答题新疆维吾尔自治区喀什地区巴楚县2024-2025学年高一上学期10月期中考试数学试题江苏省扬州市扬州大学附属中学东部分校2023-2024学年高一上学期期中考试数学试卷广州市白云区广州空港实验中学2024-2025学年高一上学期期中考试数学试题
名校
解题方法
7 . 已知函数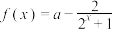 ,
, 的图像关于点
的图像关于点 中心对称.
中心对称.
(1)求实数 的值:
的值:
(2)探究 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(3)解关于 的不等式
的不等式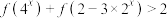 .
.
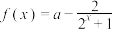 ,
, 的图像关于点
的图像关于点 中心对称.
中心对称.(1)求实数
 的值:
的值:(2)探究
 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)解关于
 的不等式
的不等式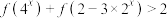 .
.
您最近一年使用:0次
2024-01-17更新
|
729次组卷
|
2卷引用:四川省隆昌市第一中学2023-2024学年高一下学期开学考试数学试题
名校
解题方法
8 . 设函数 是增函数,对于任意
是增函数,对于任意 ,
,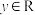 都有
都有 .
.
(1)证明 是奇函数;
是奇函数;
(2)关于 的不等式
的不等式 的解集中恰有3个正整数,求实数
的解集中恰有3个正整数,求实数 的取值范围.
的取值范围.
 是增函数,对于任意
是增函数,对于任意 ,
,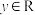 都有
都有 .
.(1)证明
 是奇函数;
是奇函数;(2)关于
 的不等式
的不等式 的解集中恰有3个正整数,求实数
的解集中恰有3个正整数,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-29更新
|
419次组卷
|
2卷引用:四川省内江市第六中学2023-2024学年高一上学期第二次月考数学试题
名校
解题方法
9 . 已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且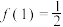 .
.
(1)求函数 的解析式;
的解析式;
(2)若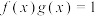 ,试用单调性的定义证明函数
,试用单调性的定义证明函数 在
在 上单调递减.
上单调递减.
 是定义在
是定义在 上的奇函数,且
上的奇函数,且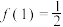 .
.(1)求函数
 的解析式;
的解析式;(2)若
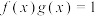 ,试用单调性的定义证明函数
,试用单调性的定义证明函数 在
在 上单调递减.
上单调递减.
您最近一年使用:0次
2023-02-21更新
|
527次组卷
|
2卷引用:四川省内江市第六中学2023-2024学年高一上学期期中考试数学试卷
10-11高二下·黑龙江鹤岗·期末
名校
解题方法
10 . 已知函数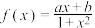 是定义在
是定义在 上的函数,
上的函数, 恒成立,且
恒成立,且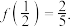
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
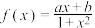 是定义在
是定义在 上的函数,
上的函数, 恒成立,且
恒成立,且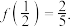
(1)确定函数
 的解析式;
的解析式;(2)用定义证明
 在
在 上是增函数;
上是增函数;(3)解不等式
 .
.
您最近一年使用:0次
2023-02-21更新
|
2468次组卷
|
154卷引用:四川省内江市第六中学2022-2023学年高一上学期第一次月考数学试卷(创新班)
四川省内江市第六中学2022-2023学年高一上学期第一次月考数学试卷(创新班)(已下线)黑龙江省鹤岗一中2010-2011学年高二下学期期末考试数学(理)(已下线)2011-2012学年度辽宁省沈阳市高三数学质量检测试卷(已下线)2011年四川省成都市六校协作体高一上学期期中考试数学(已下线)2011—2012学年江苏省仪征中学第二学期期中文科数学试卷(已下线)2011-2012学年云南省会泽县茚旺高级中学高一上学期期中数学试卷(已下线)2012-2013学年甘肃省甘谷一中高一上学期期中考试数学试题2014-2015学年山东省潍坊市第一中学高一上学期10月月考数学试卷2014-2015学年山东省潍坊市一中高一10月月考数学试卷2015-2016学年河南省郑州外国语学校高一上期第一次月考数学试卷2015-2016学年河北省枣强中学高一上学期第一次月考数学试卷2015-2016学年甘肃省定西市通渭二中高一上学期第一次月考数学试卷2015-2016学年贵州省贵阳市六中高一上期中数学试卷2015-2016学年安徽省淮南市高一上学期期末数学试卷2016-2017学年山西大同一中高一上学期期中数学试卷湖南省岳阳县一中2016-2017学年高一下学期期中考试数学试题河南省郑州外国语学校2017-2018学年高一上学期期中考试数学试卷宁夏石嘴山市第三中学2017-2018学年高一上学期期中考试数学试题【全国百强校】青海省西宁市第四高级中学2018-2019学年高一上学期第三次(12月)月考数学试题(已下线)2018年12月21日 《每日一题》人教必修1+必修2(上学期期末复习)-单调性与最大(小)值【市级联考】四川省广安市2018-2019学年高一(上)期末数学试题河南省洛阳市第一高级中学2019-2020学年高一9月月考数学试题浙江省台州五校联考2019年9月高一阶段性考试数学试题江苏省南通市第一中学2019-2020学年高一上学期10月月考数学试题四川省成都市双流区棠湖中学2019-2020学年高一上学期第一次月考数学试题北京市第八十中学2019-2020学年高一上学期期中数学试题山东省泰安市宁阳一中2019-2020学年高一上学期模块考试数学试题河北省邢台市第八中学2019-2020学年高一上学期期中数学试题江西省上饶市“山江湖”协作体2019-2020学年高一上学期期中联考数学(统招班)试题江西省宜春市宜丰县二中2019-2020学年高一上学期期中数学试题四川省自贡市田家炳中学2019-2020学年高一上学期期中数学试题山西省晋中市祁县第二中学2019-2020学年高一上学期期中数学试题福建省厦门市湖滨中学2019-2020学年高一上学期期中数学试题甘肃省天水市第一中学2019-2020学年高一上学期11月月考数学试题2江苏省苏州市吴县中学2019-2020学年高一上学期第一次调研数学试题黑龙江省绥化市青冈县第一中学2019-2020学年高一上学期(A班)期中数学试题湖北省黄石市育英高级中学2019-2020学年高一上学期9月月考数学试题山西省运城市永济中学2019-2020学年高一上学期10月月考数学试题吉林省延边州汪清县四中2019-2020学年高一上学期第一次阶段考试数学试题湖南省常德市临澧一中2019-2020学年高一上学期第一次阶段性考试数学试题四川省遂宁市第二中学2019-2020学年高一上学期期中数学试题四川省广元市川师大万达中学2019-2020学年高一上学期期中数学试题(已下线)【新东方】杭州高一数学试卷227新疆昌吉州教育共同体2019-2020学年高一上学期期末数学试题(已下线)2019-2020学年高一上学期期末复习1月第01期(考点03)-《新题速递·数学》陕西省西安交大附中2019-2020学年高一上学期9月月考数学试题江苏省南通市启东中学2017-2018学年高一下学期期初数学试题山西省河津市第二中学2019-2020学年高一上学期11月月考数学试题甘肃省武威市民勤县第一中学2018-2019学年高一上学期期中数学试题内蒙古呼和浩特市开来中学2019-2020学年高二第二学期期末考试数学(文科)试卷人教A版(2019) 必修第一册(上) 重难点知识清单 第三章 函数的概念与性质 3.2 函数的基本性质 3.2.2 奇偶性(已下线)对点练10 函数的基本性质之单调性-2020-2021年新高考高中数学一轮复习对点练(已下线)专题2.3 函数的奇偶性与周期性(精讲)-2021届高考数学(文)一轮复习讲练测(已下线)3.2.2+奇偶性-2020-2021学年高一数学新教材配套学案(人教A版必修第一册)(已下线)3.1.3+第2课时+函数奇偶性的应用(课后作业,)-新教材2020-2021学年高一数学同步备课(人教B版必修第一册)(已下线)3.2.2函数的奇偶性的应用-【新教材】人教A版(2019)高中数学必修第一册同步练习广西兴安县第三中学2018-2019学年高一上学期期中考试数学试题吉林省白城市洮南市第一中学2020-2021学年高三上学期第一次月考数学文科试卷(已下线)第5章+函数概念与性质(能力提升)-2020-2021学年高一数学单元测试定心卷(苏教版2019必修第一册)(已下线)【新东方】杭州新东方高中数学试卷345吉林省汪清县第六中学2020-2021学年高一上学期期中考试数学试题广东省韶关市田家炳中学2020-2021学年高一上学期期中数学试题广西南宁市第二十六中学2020-2021学年高一上学期段考数学试题江苏省南通市海门中学2020-2021学年高一上学期期中数学试题甘肃省民勤县第一中学2020-2021学年度第一学期高一第一次月考试题数学试题福建省福州市平潭县新世纪学校2020-2021学年高一上学期期中考试数学试题(B卷)四川省眉山市东坡区多悦高级中学校2020-2021学年高一上学期期中数学试题江苏省苏州市新区实验中学2020-2021学年高一上学期期中数学试题山东省济宁市任城区2020-2021学年高一上学期期中考试数学试题四川省成都市温江区东辰外国语学校2020-2021学年高一上学期10月月考数学试题湖北省荆州市沙市中学2020-2021学年高一上学期期中数学试题湖南省岳阳市平江县第一中学2020-2021学年高一上学期期末数学试题(已下线)3.2 函数的性质(精练)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教版A版)江苏省扬州市第一中学2020-2021学年高一上学期教学质量调研评(2)数学试题广西百色市平果县第二中学2019-2020学年高一10月月考数学试题(已下线)第二章 函数(能力提升)-2020-2021学年高一数学单元测试定心卷(北师大版必修1)(已下线)【新东方】【2021.4.27】【宁波】【高一上】【高中数学】【00109】(已下线)【新东方】【2021.5.25】【NB】【高一上】【高中数学】【NB00096】江苏省泰州市靖江市斜桥中学与刘国钧中学2020-2021学年高一上学期联考数学试题辽宁省葫芦岛市第八高级中学2020-2021学年高一实验班下学期期初考试数学试题江苏省南通市如皋市第一中学2020-2021学年高一上学期调研测试2数学试题3.2.2 第2课时 奇偶性的应用(学案)-2021-2022学年高一数学教材配套学案+练习(人教A版2019必修第一册)陕西省宝鸡市金台区2020-2021学年高二下学期期末文科数学试题江苏省淮安市盱眙县马坝高级中学城区分校2020-2021学年高三上学期阶段测试一数学试题(已下线)专练24 函数的奇偶性-2021-2022学年高一数学上册同步课后专练(人版A版必修第一册)(已下线)第3章 函数概念与性质 章末测试(基础)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第一册)(已下线)专题23 《函数的概念与性质》单元测试卷 - 2021-2022高一上学期数学新教材配套提升训练(人教B版2019必修第一册)(已下线)第三章 函数的概念与性质-2021-2022学年高一数学新教材单元过关测评卷(人教A版2019必修第一册)【学科网名师堂】云南省富源县第六中学2020-2021学年高一上学期数学期末模拟测试题河南省南阳市第一中学校2021-2022学年高三上学期第一次月考数学(文)试题河南省南阳市第一中学校2021-2022学年高三上学期第一次月考数学(理)试题河北省张家口市第一中学2020-2021学年高一上学期12月月考数学试题(已下线)考点04 函数的基本性质-备战2022年高考数学一轮复习考点帮(浙江专用)甘肃省会宁县第一中学2020-2021学年高一上学期第二次月考数学试题(已下线)第三章 函数 3.1 函数的概念与性质 3.1.3 函数的概念与性质(已下线)5.4 函数的奇偶性四川省雅安市雨城区雅安中学2021-2022学年高一上学期10月月考数学试题广东省佛山市南海区里水高级中学2021-2022学年高一上学期第一次教学质量检测数学试题广东侨中2021-2022学年高一上学期期中数学试题湖北省宜昌市葛洲坝中学2021-2022学年高一上学期期中数学试题宁夏银川一中2021-2022学年高一上学期期中考试数学试题重庆市涪陵第二中学校2021-2022学年高一上学期第二次月考数学试题(已下线)第五章 函数的概念与性质(单元测试)-【上好课】2021-2022学年高一数学同步备课系列(苏教版2019必修第一册)(已下线)期中考测试卷(基础)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第一册)(已下线)第5章 函数概念与性质 单元综合检测(重点)(单元培优)-2021-2022学年高一数学课后培优练(苏教版2019必修第一册)(已下线)第五章 函数概念与性质核心专项练习-【提升专练】2021-2022学年高一数学新教材同步学案+课时对点练(苏教版2019必修第一册)(已下线)专题14 函数的概念与性质压轴题型汇总-2021-2022学年高一《新题速递·数学》(人教A版2019)福建省龙岩市第一中学锦山学校2021-2022学年高一上学期第三次阶段性考试数学试题宁夏石嘴山市平罗中学2021-2022学年高一上学期期末考试数学试题青海省西宁市2021-2022学年高一上学期期末数学试题(已下线)第1讲 函数的图象与性质(练 )-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)(已下线)专题3.5 函数的概念与性质章节测试(A)-《聚能闯关》2021-2022学年高一数学提优闯关训练(人教A版2019必修第一册)河南省南阳市社旗县第一高级中学2021-2022学年高一(实验班)上学期入学测试数学试题江苏省常州市武进高级中学2021-2022学年高二上学期阶段检测数学试题新疆乌鲁木齐市第一中学2021-2022学年高一上学期期末数学试题(已下线)专题07 《函数概念与性质》中的解答题压轴题(1)-2021-2022学年高一数学上册同步培优训练系列(苏教版2019)四川省攀枝花市第七高级中学校2021-2022学年高一上学期第一次月考数学试题黑龙江省齐齐哈尔市恒昌中学校2021-2022学年高一上学期期中考试数学试题陕西省西安市雁塔区第二中学、渭北中学2021-2022学年高二下学期期中联考文科数学试题(已下线)专题07 函数的性质-单调性、奇偶性、周期性河北省武强中学2021-2022学年高二下学期期末数学试题黑龙江省七台河市勃利县高级中学2021-2022学年高一上学期期末考试数学试题(已下线)专题19 函数的基本性质(3)第三章 函数的概念与性质(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第一册)第五章 函数概念与性质(B卷·能力提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(苏教版2019必修第一册)江西省赣州市赣县第三中学2022届高三上学期强化训练(四)数学(理)试题广东省广州科学城中学2022-2023学年高一上学期期中数学试题黑龙江省佳木斯市桦南县第一中学2022-2023学年高一上学期期中数学试题广东省广州市执信中学2022-2023学年高一上学期期中数学试题广东省广州市十六中2022-2023学年高一上学期期中数学试题甘肃省兰州市第六十三中学2022-2023学年高一上学期期中数学试题辽宁省锦州市第一高级中学2022-2023学年高一上学期期中考试数学试题广东华侨中学2022-2023学年高一上学期期中数学试题吉林省长白朝鲜族自治县实验中学2022-2023学年高一上学期第二次月考数试题河南省郑州市六校联盟2022-2023学年高一上学期期中考试数学试题吉林省吉林市吉林毓文中学2018-2019学年高一上第一次月考数学试题吉林省松原市乾安县第七中学2021-2022学年高一上学期第三次质量检测数学试题陕西省铜川市耀州中学2022-2023学年高一上学期期末数学试题重庆市荣昌永荣中学校2021-2022学年高二下学期期末数学试题湖北省天门市2019-2020学年高一上学期11月月考数学试题广东省河源市源城区城东学校2022-2023学年高一上学期11月月考数学试题湖南省株洲市炎陵县2022-2023学年高一下学期3月素质检测数学试题吉林省长春市第十七中学2022-2023学年高二下学期4月月考数学试题(已下线)专题07 函数的性质-单调性、奇偶性、周期性-4 云南省丽江市2022-2023学年高一上学期期末考试数学试题3.2.1函数的单调性与最值第三章 函数 单元检测卷-2022-2023学年高一上学期数学人教B版(2019)必修第一册湖北省武汉市黄陂一中盘龙校区2022-2023学年高一上学期11月适应性考试数学试题宁夏银川市贺兰县景博中学2022-2023学年高一上学期期中考试数学试题广东省惠州市龙门县高级中学2023-2024学年高一上学期期中考试数学试题吉林省普通高中友好学校联合体2023-2024学年高一上学期第三十七届基础年段期末联考数学试题(已下线)第三章 函数的概念与性质(单元检测)-【同步题型讲义】(人教A版2019必修第一册)黑龙江省齐齐哈尔市衡齐高级中学2024-2025学年高一上学期9月月考数学试题河南省安阳市安阳县实验中学2022-2023学年高一上学期开学考试数学试题



