解题方法
1 . 已知函数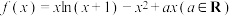 .
.
(1)若 在定义域内是单调函数,求a的取值范围;
在定义域内是单调函数,求a的取值范围;
(2)若 有两个极值点
有两个极值点 ,
, ,求证:
,求证: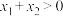 .
.
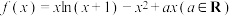 .
.(1)若
 在定义域内是单调函数,求a的取值范围;
在定义域内是单调函数,求a的取值范围;(2)若
 有两个极值点
有两个极值点 ,
, ,求证:
,求证: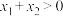 .
.
您最近一年使用:0次
2024-07-03更新
|
258次组卷
|
2卷引用:2024届西藏自治区高三5月大联考理科数学试卷
2 . 已知直线 的参数方程为
的参数方程为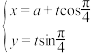 (
( 为参数,
为参数, ).以坐标原点
).以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为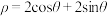 .
.
(1)写出直线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(2)设 是曲线
是曲线 上的两点,且
上的两点,且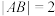 .若直线
.若直线 上存在点
上存在点 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
 的参数方程为
的参数方程为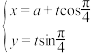 (
( 为参数,
为参数, ).以坐标原点
).以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为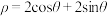 .
.(1)写出直线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)设
 是曲线
是曲线 上的两点,且
上的两点,且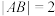 .若直线
.若直线 上存在点
上存在点 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-03更新
|
105次组卷
|
3卷引用:西藏自治区拉萨市第三高级中学2023-2024学年高三下学期5月月考文科数学试题
名校
3 . 已知函数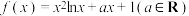 .
.
(1)若曲线 在点
在点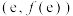 处的切线与直线
处的切线与直线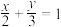 平行,求实数
平行,求实数 的值;
的值;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
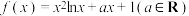 .
.(1)若曲线
 在点
在点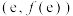 处的切线与直线
处的切线与直线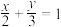 平行,求实数
平行,求实数 的值;
的值;(2)若
 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
4 . 已知抛物线 ,准线
,准线 与
与 轴交于点
轴交于点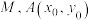 为抛物线
为抛物线 上一点,
上一点, 交
交 轴于点
轴于点 .当
.当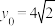 时,
时, .
.
(1)求抛物线 的方程;
的方程;
(2)设直线 与抛物线
与抛物线 的另一交点为
的另一交点为 (点
(点 在点
在点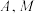 之间),过点
之间),过点 且垂直于
且垂直于 轴的直线交
轴的直线交 于点
于点 .是否存在实数
.是否存在实数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 ,准线
,准线 与
与 轴交于点
轴交于点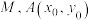 为抛物线
为抛物线 上一点,
上一点, 交
交 轴于点
轴于点 .当
.当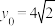 时,
时, .
.(1)求抛物线
 的方程;
的方程;(2)设直线
 与抛物线
与抛物线 的另一交点为
的另一交点为 (点
(点 在点
在点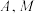 之间),过点
之间),过点 且垂直于
且垂直于 轴的直线交
轴的直线交 于点
于点 .是否存在实数
.是否存在实数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2024-06-25更新
|
359次组卷
|
5卷引用:西藏自治区拉萨市第三高级中学2023-2024学年高三下学期5月月考文科数学试题
名校
解题方法
5 . 已知函数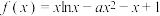 .
.
(1)若 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;
(2)若 有两个极值点
有两个极值点 ,
, ,证明:
,证明: .
.
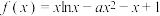 .
.(1)若
 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;(2)若
 有两个极值点
有两个极值点 ,
, ,证明:
,证明: .
.
您最近一年使用:0次
2023-11-28更新
|
679次组卷
|
5卷引用:西藏拉萨市城关区拉萨中学2024届高三第五次月考数学(文)试题
名校
解题方法
6 . 已知函数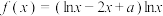 .
.
(1)当 时,求
时,求 的单调性;
的单调性;
(2)若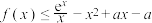 ,求实数
,求实数 的取值范围.
的取值范围.
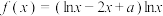 .
.(1)当
 时,求
时,求 的单调性;
的单调性;(2)若
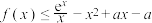 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-03更新
|
906次组卷
|
6卷引用:西藏林芝市第二高级中学2024届高三上学期第三次月考数学(理)试题
7 . 已知函数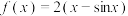 .
.
(1)判断函数 的单调性;
的单调性;
(2)已知函数 ,其中
,其中 ,若存在
,若存在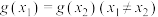 ,证明:
,证明: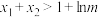 .
.
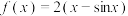 .
.(1)判断函数
 的单调性;
的单调性;(2)已知函数
 ,其中
,其中 ,若存在
,若存在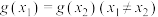 ,证明:
,证明: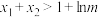 .
.
您最近一年使用:0次
8 . 已知函数 .
.
(1)若函数 在点
在点 处的切线与函数
处的切线与函数 的图象有公共点,求实数
的图象有公共点,求实数 的取值范围;
的取值范围;
(2)若函数 和函数
和函数 的图象没有公共点,求实数
的图象没有公共点,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 在点
在点 处的切线与函数
处的切线与函数 的图象有公共点,求实数
的图象有公共点,求实数 的取值范围;
的取值范围;(2)若函数
 和函数
和函数 的图象没有公共点,求实数
的图象没有公共点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
9 . 已知双曲线C: 的离心率为
的离心率为 ,F为C的左焦点,P是C右支上的点,点P到C的两条渐近线的距离之积为
,F为C的左焦点,P是C右支上的点,点P到C的两条渐近线的距离之积为 .
.
(1)求C的方程;
(2)若线段PF与C的左支交于点Q,与两条渐近线交于点A,B,且 ,求
,求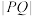 .
.
 的离心率为
的离心率为 ,F为C的左焦点,P是C右支上的点,点P到C的两条渐近线的距离之积为
,F为C的左焦点,P是C右支上的点,点P到C的两条渐近线的距离之积为 .
.(1)求C的方程;
(2)若线段PF与C的左支交于点Q,与两条渐近线交于点A,B,且
 ,求
,求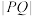 .
.
您最近一年使用:0次
名校
解题方法
10 . 已知函数 .
.
(1)若 ,求
,求 的最小值;
的最小值;
(2)若方程 有解,求实数a的取值范围.
有解,求实数a的取值范围.
 .
.(1)若
 ,求
,求 的最小值;
的最小值;(2)若方程
 有解,求实数a的取值范围.
有解,求实数a的取值范围.
您最近一年使用:0次
2023-08-13更新
|
639次组卷
|
5卷引用:西藏自治区拉萨市2024届高三一模数学(理)试题



