1 . 已知函数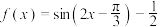 .
.
(1)求函数 的单调递增区间,并解不等式
的单调递增区间,并解不等式 ;
;
(2)关于 的方程
的方程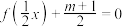 在
在 上有两个不相等的实数解
上有两个不相等的实数解 ,求实数
,求实数 的取值范围及
的取值范围及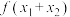 的值.
的值.
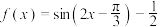 .
.(1)求函数
 的单调递增区间,并解不等式
的单调递增区间,并解不等式 ;
;(2)关于
 的方程
的方程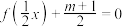 在
在 上有两个不相等的实数解
上有两个不相等的实数解 ,求实数
,求实数 的取值范围及
的取值范围及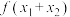 的值.
的值.
您最近一年使用:0次
2024-02-11更新
|
609次组卷
|
3卷引用:四川省绵阳市2023-2024学年高一上期末教学质量测试数学试卷
四川省绵阳市2023-2024学年高一上期末教学质量测试数学试卷安徽省六安市第二中学2023-2024学年高一上学期期末数学试题(一)(已下线)【第三练】5.4.1正弦函数、余弦函数的图象+5.4.2正弦函数、余弦函数的性质
解题方法
2 . 已知函数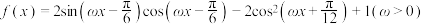 ,且满足________.
,且满足________.
(1)求函数 的解析式;
的解析式;
(2)若关于x的方程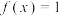 在区间
在区间 上有两个不同解,求实数m的取值范围.
上有两个不同解,求实数m的取值范围.
从① 的图象与直线
的图象与直线 的两个相邻交点之间的距离等于
的两个相邻交点之间的距离等于 ;②
;② 的两个相邻对称中心之间的距离为
的两个相邻对称中心之间的距离为 .这两个条件中选择一个,补充在上面问题中并作答.
.这两个条件中选择一个,补充在上面问题中并作答.
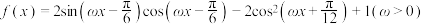 ,且满足________.
,且满足________.(1)求函数
 的解析式;
的解析式;(2)若关于x的方程
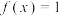 在区间
在区间 上有两个不同解,求实数m的取值范围.
上有两个不同解,求实数m的取值范围.从①
 的图象与直线
的图象与直线 的两个相邻交点之间的距离等于
的两个相邻交点之间的距离等于 ;②
;② 的两个相邻对称中心之间的距离为
的两个相邻对称中心之间的距离为 .这两个条件中选择一个,补充在上面问题中并作答.
.这两个条件中选择一个,补充在上面问题中并作答.
您最近一年使用:0次
名校
解题方法
3 . 在平面直角坐标系 中,角
中,角 的始边为
的始边为 轴的非负半轴,终边经过点
轴的非负半轴,终边经过点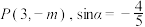
(1)求 的值和
的值和 ;
;
(2)化简求值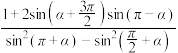
 中,角
中,角 的始边为
的始边为 轴的非负半轴,终边经过点
轴的非负半轴,终边经过点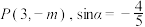
(1)求
 的值和
的值和 ;
;(2)化简求值
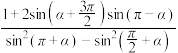
您最近一年使用:0次
2024-01-21更新
|
917次组卷
|
3卷引用:四川省宜宾市叙州区第二中学校2023-2024学年高一上学期期末数学试题
名校
解题方法
4 . 已知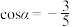 ,且
,且 是第二象限角.
是第二象限角.
(1)求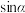 ,
, 的值;
的值;
(2)化简求值: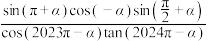 .
.
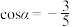 ,且
,且 是第二象限角.
是第二象限角.(1)求
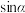 ,
, 的值;
的值;(2)化简求值:
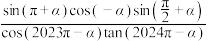 .
.
您最近一年使用:0次
2023-07-11更新
|
640次组卷
|
2卷引用:四川省内江市2022-2023学年高一下学期期末数学试题
解题方法
5 . 化简求值:
(1)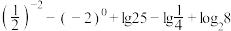 ;
;
(2)已知 ,求
,求 .
.
(1)
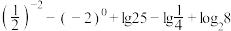 ;
;(2)已知
 ,求
,求 .
.
您最近一年使用:0次
6 . 已知函数f(x)=sinx(x∈R),则下列四个说法:
①函数g(x)=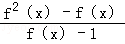 是奇函数;
是奇函数;
②函数f(x)满足:对任意x1,x2∈[0,π]且x1≠x2都有f(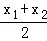 )<
)<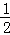 [f(x1)+f(x2)];
[f(x1)+f(x2)];
③若关于x的不等式f2(x)﹣f(x)+a≤0在R上有解,则实数a的取值范围是(﹣∞,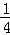 ];
];
④若关于x的方程3﹣2cos2x=f(x)﹣a在[0,π]恰有4个不相等的解x1,x2,x3,x4;则实数a的取值范围是[﹣1,﹣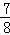 ),且x1+x2+x3+x4=2π;
),且x1+x2+x3+x4=2π;
其中说法正确的序号是_____ .
①函数g(x)=
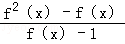 是奇函数;
是奇函数;②函数f(x)满足:对任意x1,x2∈[0,π]且x1≠x2都有f(
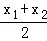 )<
)<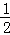 [f(x1)+f(x2)];
[f(x1)+f(x2)];③若关于x的不等式f2(x)﹣f(x)+a≤0在R上有解,则实数a的取值范围是(﹣∞,
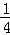 ];
];④若关于x的方程3﹣2cos2x=f(x)﹣a在[0,π]恰有4个不相等的解x1,x2,x3,x4;则实数a的取值范围是[﹣1,﹣
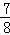 ),且x1+x2+x3+x4=2π;
),且x1+x2+x3+x4=2π;其中说法正确的序号是
您最近一年使用:0次
7 . 化简或计算下列各题:
(Ⅰ)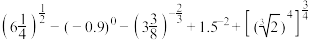 ;
;
(Ⅱ)已知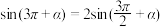 ,求
,求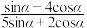
(Ⅰ)
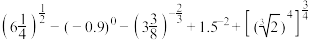 ;
;(Ⅱ)已知
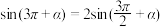 ,求
,求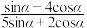
您最近一年使用:0次
11-12高一下·浙江杭州·阶段练习
名校
解题方法
8 . 已知函数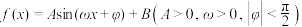 的某一周期内的对应值如下表:
的某一周期内的对应值如下表:
(1)根据表格提供的数据求函数 的解析式;
的解析式;
(2)根据(1)的结果,若函数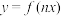 ,
, 的最小正周期为
的最小正周期为 ,当
,当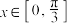 时,方程
时,方程 恰有两个不同的解,求实数m的取值范围.
恰有两个不同的解,求实数m的取值范围.
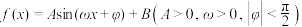 的某一周期内的对应值如下表:
的某一周期内的对应值如下表:| x | 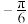 |  |  |  |  |
 |  | 1 | 3 | 1 |  |
 的解析式;
的解析式;(2)根据(1)的结果,若函数
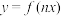 ,
, 的最小正周期为
的最小正周期为 ,当
,当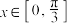 时,方程
时,方程 恰有两个不同的解,求实数m的取值范围.
恰有两个不同的解,求实数m的取值范围.
您最近一年使用:0次
2023-12-14更新
|
711次组卷
|
41卷引用:四川省巴中市恩阳区2020-2021学年高一上学期期末数学试题
四川省巴中市恩阳区2020-2021学年高一上学期期末数学试题黑龙江省鹤岗市第一中学2020-2021学年高一上学期期末考试数学试题福建省莆田第七中学2020-2021学年高一上学期期末考试数学试题(已下线)期末押题测试卷(一)-《聚能闯关》2021-2022学年高一数学提优闯关训练(人教A版2019必修第一册)浙江省宁波市镇海中学2021-2022学年高一上学期期末数学试题山东省青岛市青岛第九中学2021-2022学年高一上学期期末数学试题河南省漯河市第五高级中学2022-2023学年高一上学期期末数学试题四川省绵阳市三台县三台中学校2022-2023学年高一下学期3月月考数学试题(已下线)2011-2012学年浙江省杭州市西湖高级中学高一3月月考数学试卷(已下线)2012-2013学年安徽省泗县二中高一上学期第三次月考数学试卷(已下线)2013-2014学年山东省淄博六中高二下学期期中考试文科数学试卷(已下线)2013-2014学年浙江省巨人中学等三校高一下学期第二次联考数学试卷2015-2016学年浙江慈溪中学高一7-12班上期中数学卷江西省樟树中学2017-2018学年人教A版高一下学期第一次月考数学(理)试题人教高中数学 必修四 1.4 三角函数图像与性质试题(已下线)2019年一轮复习讲练测【新课标版理】 4.4三角函数的图象及三角函数模型的简单应用【测】(已下线)2019年一轮复习讲练测【新课标版文】4.4三角函数的图象及三角函数模型的简单应用【测】人教A版 必杀技 第一章 三角函数 第一章全章训练湖南省长沙市南雅中学2019-2020学年高一上学期12月月考数学试题第五章 三角函数 本章达标检测人教B版(2019) 必修第三册 逆袭之路 第七章 三角函数 整合提升人教A版(2019) 必修第一册 必杀技 第五章 素养检测河南省林州市第一中学2019-2020学年高一3月线上考试数学试题专题15 三角函数的图象与性质(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第一册)-《高中新教材知识讲学》(已下线)专题02 三角函数的图象问题(第一篇)-备战2020年高考数学大题精做之解答题题型全覆盖陕西省咸阳市武功县普集高中2019-2020学年高一下学期第二次月考数学试题河南省项城三高2019-2020学年高一下学期第一次调研考试数学试题(已下线)综合测试(一)-2020-2021学年高一数学尖子生同步培优题典(人教A版2019必修第一册)(已下线)综合测试(二)-2020-2021学年高一数学尖子生同步培优题典(人教A版2019必修第一册)宁夏回族自治区银川一中2021届高三上学期第一次月考数学(文)试题江西省信丰中学2019-2020学年高一上学期第二次月考数学试题吉林省白城市洮南市第一中学2020-2021学年高三上学期第一次月考数学文科试卷(已下线)5.6+第1课时+函数y=Asin(ωx+φ)(一)(分层练习)-2020-2021学年高一数学新教材配套练习(人教A版必修第一册)河南省新乡县高级中学2020-2021学年高一下学期第二次月考数学试题(已下线)第7章 三角函数(A卷·夯实基础)-2021-2022学年高一数学同步单元AB卷(苏教版2019必修第一册)【学科网名师堂】甘肃省兰州市教育局第四片区2021-2022学年高一下学期期中考试数学试题(已下线)第7章 三角函数(基础卷)-【满分计划】2022-2023学年高一数学阶段性复习测试卷(苏教版2019必修第一册)第五章 三角函数单元检测(已下线)第七章 三角函数(单元重点综合测试)单元速记·巧练(苏教版2019必修第一册)(已下线)5.6函数y=Asin(ωx+φ)(导学案)-【上好课】河北省保定市第一中学2024-2025学年高一(第八届贯通班)上学期开学考试数学试题
名校
9 . 已知平面向量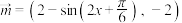 ,
,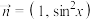 ,
, ,其中
,其中 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象所有的点向右平移
的图象所有的点向右平移 个单位,再将所得图象上各点横坐标缩短为原来的
个单位,再将所得图象上各点横坐标缩短为原来的 (纵坐标不变),再向下平移1个单位得到
(纵坐标不变),再向下平移1个单位得到 的图象,若
的图象,若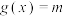 在
在 上恰有2个解,求m的取值范围.
上恰有2个解,求m的取值范围.
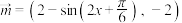 ,
,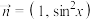 ,
, ,其中
,其中 .
.(1)求函数
 的单调增区间;
的单调增区间;(2)将函数
 的图象所有的点向右平移
的图象所有的点向右平移 个单位,再将所得图象上各点横坐标缩短为原来的
个单位,再将所得图象上各点横坐标缩短为原来的 (纵坐标不变),再向下平移1个单位得到
(纵坐标不变),再向下平移1个单位得到 的图象,若
的图象,若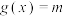 在
在 上恰有2个解,求m的取值范围.
上恰有2个解,求m的取值范围.
您最近一年使用:0次
2022-06-06更新
|
2035次组卷
|
8卷引用:四川省仁寿第一中学校南校区2022-2023学年高一下学期期末适应性考试数学试题
四川省仁寿第一中学校南校区2022-2023学年高一下学期期末适应性考试数学试题四川省内江市内江市第六中学2022-2023学年高一下学期期中数学试题广东省珠海市香樟中学2022-2023学年高一下学期期末数学试题云南省昆明市第一中学2021-2022学年高一下学期期中考试数学试题(已下线)第08讲:第四章 三角函数(测)(提高卷)-2023年高考数学一轮复习讲练测(新教材新高考)(已下线)专题4-4 三角函数与解三角形大题综合归类-1(已下线)拓展一:平面向量的拓展应用 (精讲)(2) - 【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)云南省临沧市民族中学2022-2023学年高二上学期期中数学试题
名校
解题方法
10 . 已知函数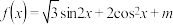 在区间
在区间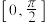 上的最大值为6.
上的最大值为6.
(1)求常数 的值以及函数
的值以及函数 当
当 时的最小值
时的最小值
(2)将函数 的图象向下平移4个单位,再向右平移
的图象向下平移4个单位,再向右平移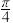 个单位,得到函数
个单位,得到函数 的图象
的图象
(i)求函数 的解析式;
的解析式;
(ii)若关于 的方程
的方程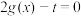 在
在 时,有两个不同实数解,求实数
时,有两个不同实数解,求实数 的取值范围.
的取值范围.
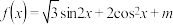 在区间
在区间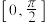 上的最大值为6.
上的最大值为6.(1)求常数
 的值以及函数
的值以及函数 当
当 时的最小值
时的最小值(2)将函数
 的图象向下平移4个单位,再向右平移
的图象向下平移4个单位,再向右平移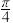 个单位,得到函数
个单位,得到函数 的图象
的图象(i)求函数
 的解析式;
的解析式;(ii)若关于
 的方程
的方程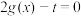 在
在 时,有两个不同实数解,求实数
时,有两个不同实数解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-03-22更新
|
1530次组卷
|
3卷引用:四川省自贡市2020-2021学年高一上学期期末数学试题



