1 . 四棱锥 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,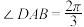 .
.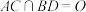 ,且
,且 平面
平面 ,
,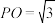 ,点
,点 分别是线段
分别是线段 上的中点,
上的中点, 在
在 上.且
上.且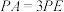 .
.
(Ⅰ)求证: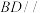 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 的成角的正弦值;
的成角的正弦值;
(Ⅲ)请画出平面 与四棱锥的表面的交线,并写出作图的步骤.
与四棱锥的表面的交线,并写出作图的步骤.
 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,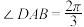 .
.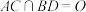 ,且
,且 平面
平面 ,
,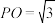 ,点
,点 分别是线段
分别是线段 上的中点,
上的中点, 在
在 上.且
上.且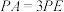 .
.(Ⅰ)求证:
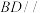 平面
平面 ;
;(Ⅱ)求直线
 与平面
与平面 的成角的正弦值;
的成角的正弦值;(Ⅲ)请画出平面
 与四棱锥的表面的交线,并写出作图的步骤.
与四棱锥的表面的交线,并写出作图的步骤.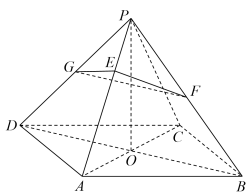
您最近一年使用:0次
2018-06-16更新
|
1431次组卷
|
7卷引用:【全国百强校】北京市十一学校2018届高三三模数学(文理)试题
【全国百强校】北京市十一学校2018届高三三模数学(文理)试题北京市十一学校2024届高三下学期三模数学试题(已下线)专题24 立体几何解答题最全归纳总结-2(已下线)专题08 立体几何解答题常考全归类(精讲精练)-1(已下线)重难点突破06 立体几何解答题最全归纳总结(九大题型)-2(已下线)专题15 立体几何解答题全归类(练习)(已下线)重难点突破03 立体几何解答题常考模型归纳总结(九大题型)-1
名校
解题方法
2 . 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形, ,
,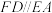 ,且
,且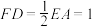 .
.

(1)记线段 的中点为
的中点为 ,在平面
,在平面 内过点
内过点 作一条直线与平面
作一条直线与平面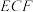 平行,要求保留作图痕迹,但不要求证明;
平行,要求保留作图痕迹,但不要求证明;
(2)求直线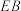 与平面
与平面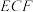 所成角的正弦值.
所成角的正弦值.
 ,
,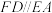 ,且
,且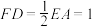 .
.
(1)记线段
 的中点为
的中点为 ,在平面
,在平面 内过点
内过点 作一条直线与平面
作一条直线与平面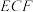 平行,要求保留作图痕迹,但不要求证明;
平行,要求保留作图痕迹,但不要求证明;(2)求直线
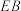 与平面
与平面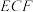 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-06-15更新
|
713次组卷
|
9卷引用:广西桂林市桂林中学2017届高三5月全程模拟考试数学(理)试题
广西桂林市桂林中学2017届高三5月全程模拟考试数学(理)试题山西省太原市第五中学2017届高三第二次模拟考试(5月) 数学(理)试题辽宁省鞍山市第一中学2018届高三上学期第二次模拟考试(期中)数学(理)试题天津市实验中学2018届高三上学期第二次模拟数学(理)试题江西省临川二中、新余四中2018届高三1月联合考试数学(理)试题安徽省舒城中学2023届高三仿真模拟卷(三)数学试题(已下线)重难点突破06 立体几何解答题最全归纳总结(九大题型)-2(已下线)专题15 立体几何解答题全归类(9大核心考点)(讲义)-1(已下线)重难点12 立体几何必考经典解答题全归类【九大题型】
名校
解题方法
3 . 如图,组合体由半个圆锥 和一个三棱锥
和一个三棱锥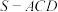 构成,其中
构成,其中 是圆锥
是圆锥 底面圆心,
底面圆心, 是圆弧
是圆弧 上一点,满足
上一点,满足 是锐角,
是锐角, .
.
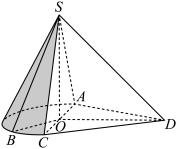
(1)在平面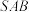 内过点
内过点 作
作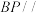 平面
平面 交
交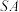 于点
于点 ,并写出作图步骤,但不要求证明;
,并写出作图步骤,但不要求证明;
(2)在(1)中,若 是
是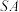 中点,且
中点,且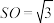 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 和一个三棱锥
和一个三棱锥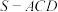 构成,其中
构成,其中 是圆锥
是圆锥 底面圆心,
底面圆心, 是圆弧
是圆弧 上一点,满足
上一点,满足 是锐角,
是锐角, .
.
(1)在平面
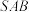 内过点
内过点 作
作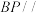 平面
平面 交
交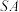 于点
于点 ,并写出作图步骤,但不要求证明;
,并写出作图步骤,但不要求证明;(2)在(1)中,若
 是
是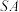 中点,且
中点,且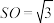 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2020-08-05更新
|
210次组卷
|
4卷引用:福建省福州第一中学2020届高三6月高考模拟考试数学(理)试题
福建省福州第一中学2020届高三6月高考模拟考试数学(理)试题福建省2020届高三考前冲刺适应性模拟卷(三)数学(理)试题(已下线)专题04 立体几何——2020年高考真题和模拟题理科数学分项汇编(已下线)考点41 立体几何的向量方法-空间角问题(考点专练)-备战2021年新高考数学一轮复习考点微专题
19-20高二下·上海浦东新·阶段练习
名校
解题方法
4 . 正四棱锥 的底面正方形边长是3,
的底面正方形边长是3, 是在底面上的射影,
是在底面上的射影,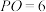 ,
, 是
是 上的一点,过
上的一点,过 且与
且与 、
、 都平行的截面为五边形
都平行的截面为五边形 .
.

(1)在图中作出截面 ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
 的底面正方形边长是3,
的底面正方形边长是3, 是在底面上的射影,
是在底面上的射影,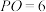 ,
, 是
是 上的一点,过
上的一点,过 且与
且与 、
、 都平行的截面为五边形
都平行的截面为五边形 .
.
(1)在图中作出截面
 ,并写出作图过程;
,并写出作图过程;(2)求该截面面积的最大值.
您最近一年使用:0次
2020-05-04更新
|
1372次组卷
|
6卷引用:2020届上海市高三高考压轴卷数学试题
2020届上海市高三高考压轴卷数学试题(已下线)上海市华东师范大学第二附属中学2019-2020学年高二下学期(4月)月考数学试题(已下线)重难点05 空间向量与立体几何-2021年高考数学【热点·重点·难点】专练(上海专用)(已下线)专题5.8 期末考前选做30题(解答题压轴版)-2020-2021学年高二数学下学期期末专项复习(沪教版)(已下线)第09讲 空间几何体的结构与直观图(核心考点讲与练)(1)(已下线)第四章 立体几何解题通法 专题一 降维法 微点1 降维法(一)【基础版】
名校
解题方法
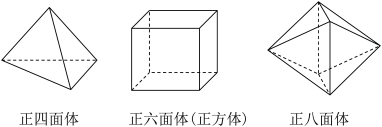
5 . 如果一个凸多面体的每个面都是全等的正多边形,而且每个顶点都引出相同数目的棱,那么这个凸多面体叫做正多面体.古希腊数学家欧几里得在其著作《几何原本》的卷13中系统地研究了正多面体的作图,并证明了每个正多面体都有外接球.若正四面体、正方体、正八面体的外接球半径相同,则它们的棱长之比为( )

A.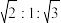 | B. | C.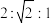 | D.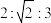 |
您最近一年使用:0次
2020-02-15更新
|
624次组卷
|
5卷引用:2020届安徽省芜湖市高三上学期期末数学(文)试题
2020届安徽省芜湖市高三上学期期末数学(文)试题陕西省咸阳市武功县普集高级中学2023届高三5月模考(三)数学(文)试题陕西省咸阳市武功县普集高级中学2023届高三5月模拟预测理科数学试题(已下线)专题4.2 与球相关的外接与内切问题-玩转压轴题,进军满分之2021高考数学选择题填空题(已下线)专题25 欧几里得
6 . 如图,在直三棱柱 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形,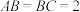 ,
, ,
, 为
为 的中点,
的中点, 为
为 的三等分点(靠近
的三等分点(靠近 )点.
)点.
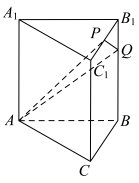
(1)求三棱锥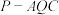 的体积;
的体积;
(2)在线段 上找点
上找点 ,使得
,使得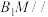 平面
平面 ,写出作图步骤,但不要求证明.
,写出作图步骤,但不要求证明.
 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形,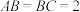 ,
, ,
, 为
为 的中点,
的中点, 为
为 的三等分点(靠近
的三等分点(靠近 )点.
)点.
(1)求三棱锥
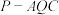 的体积;
的体积;(2)在线段
 上找点
上找点 ,使得
,使得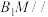 平面
平面 ,写出作图步骤,但不要求证明.
,写出作图步骤,但不要求证明.
您最近一年使用:0次
解题方法
7 . 在四棱锥 中,
中, 平面
平面 ,且底面
,且底面 为边长为2的菱形,
为边长为2的菱形,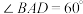 ,
,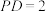 .
.
(1)记 在平面
在平面 内的射影为
内的射影为 (即
(即 平面
平面 ),试用作图的方法找出M点位置,并写出
),试用作图的方法找出M点位置,并写出 的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);
的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);
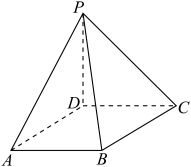
(2)求二面角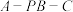 的余弦值.
的余弦值.
 中,
中, 平面
平面 ,且底面
,且底面 为边长为2的菱形,
为边长为2的菱形,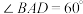 ,
,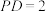 .
.(1)记
 在平面
在平面 内的射影为
内的射影为 (即
(即 平面
平面 ),试用作图的方法找出M点位置,并写出
),试用作图的方法找出M点位置,并写出 的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);
的长(要求写出作图过程,并保留作图痕迹,不需证明过程和计算过程);
(2)求二面角
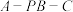 的余弦值.
的余弦值.
您最近一年使用:0次
8 . 如图,已知多面体 的底面
的底面 是边长为2的正方形,
是边长为2的正方形,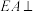 底面
底面 ,
,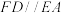 ,且
,且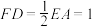 .
.
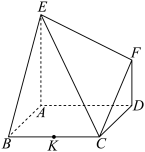
(Ⅰ)求多面体 的体积;
的体积;
(Ⅱ)求直线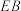 与平面
与平面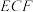 所成角的正弦值;
所成角的正弦值;
(Ⅲ)记线段 的中点为
的中点为 ,在平面
,在平面 内过点
内过点 作一条直线与平面
作一条直线与平面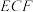 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
 的底面
的底面 是边长为2的正方形,
是边长为2的正方形,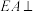 底面
底面 ,
,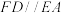 ,且
,且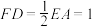 .
.
(Ⅰ)求多面体
 的体积;
的体积;(Ⅱ)求直线
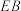 与平面
与平面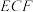 所成角的正弦值;
所成角的正弦值;(Ⅲ)记线段
 的中点为
的中点为 ,在平面
,在平面 内过点
内过点 作一条直线与平面
作一条直线与平面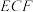 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
您最近一年使用:0次
2017-04-18更新
|
242次组卷
|
3卷引用:2017届山西省三区八校高三第二次模拟考试数学(理)试卷
名校
解题方法
9 . 如图,三棱柱 中,
中,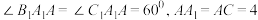 ,
, ,
, 分别为棱
分别为棱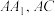 的中点.
的中点.
(1)在平面 内过点
内过点 作
作 平面
平面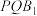 交
交 于点
于点 ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面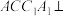 侧面
侧面 ,求直线
,求直线 与平面
与平面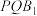 所成角的正弦值.
所成角的正弦值.
 中,
中,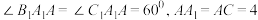 ,
, ,
, 分别为棱
分别为棱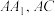 的中点.
的中点.(1)在平面
 内过点
内过点 作
作 平面
平面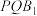 交
交 于点
于点 ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.(2)若侧面
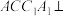 侧面
侧面 ,求直线
,求直线 与平面
与平面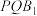 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2017-04-11更新
|
808次组卷
|
5卷引用:2017届福建省高三4月单科质量检测数学理试卷
2017届福建省高三4月单科质量检测数学理试卷江西省新余市第一中学2017届高三高考全真模拟考试数学(理)试题江西省新余市第一中学2017届高三高考全真模拟考试理科数学试题湖北武汉市蔡甸区汉阳一中2017届高三第三次模拟考试数学(理)试题(已下线)重难点突破03 立体几何解答题常考模型归纳总结(九大题型)-2
解题方法
10 . 如图,已知多面体 的底面
的底面 是边长为2的正方形,
是边长为2的正方形,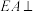 底面
底面 ,
,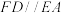 ,且
,且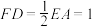 .
.
(1)求多面体 的体积;
的体积;
(2)记线段 的中点为
的中点为 ,在平面
,在平面 内过点
内过点 作一条直线与平面
作一条直线与平面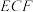 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
 的底面
的底面 是边长为2的正方形,
是边长为2的正方形,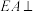 底面
底面 ,
,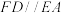 ,且
,且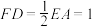 .
.
(1)求多面体
 的体积;
的体积;(2)记线段
 的中点为
的中点为 ,在平面
,在平面 内过点
内过点 作一条直线与平面
作一条直线与平面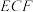 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
您最近一年使用:0次



