名校
解题方法
1 . 已知 是函数
是函数 的导函数,且对任意的实数
的导函数,且对任意的实数 都有
都有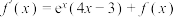 (
( 是自然对数的底数),
是自然对数的底数), ,若不等式组
,若不等式组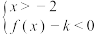 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数 的取值范围是
的取值范围是__________
 是函数
是函数 的导函数,且对任意的实数
的导函数,且对任意的实数 都有
都有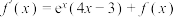 (
( 是自然对数的底数),
是自然对数的底数), ,若不等式组
,若不等式组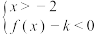 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
2 . 新教材人教B版必修第二册课后习题:“求证方程 只有一个解”.证明如下:“化为
只有一个解”.证明如下:“化为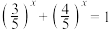 ,设
,设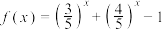 ,则
,则 在R上单调递减,且
在R上单调递减,且 ,所以原方程只有一个解
,所以原方程只有一个解 ”.类比上述解题思路,解不等式
”.类比上述解题思路,解不等式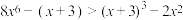 的解集是( )
的解集是( )
 只有一个解”.证明如下:“化为
只有一个解”.证明如下:“化为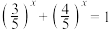 ,设
,设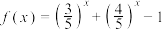 ,则
,则 在R上单调递减,且
在R上单调递减,且 ,所以原方程只有一个解
,所以原方程只有一个解 ”.类比上述解题思路,解不等式
”.类比上述解题思路,解不等式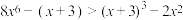 的解集是( )
的解集是( )A.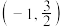 | B. |
C. | D. |
您最近一年使用:0次
2022-05-05更新
|
209次组卷
|
2卷引用:河南省商丘市商丘名校2021-2022学年高二下学期期中联考数学文科试题
3 . 对于三次函数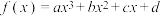
 ,给出定义:设
,给出定义:设 是函数
是函数 的导数,
的导数, 是
是 的导数,若方程
的导数,若方程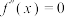 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”,同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心,若
的“拐点”,同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心,若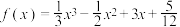 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 的对称中心为
的对称中心为___________ ;(2)计算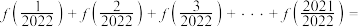
___________ .
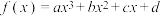
 ,给出定义:设
,给出定义:设 是函数
是函数 的导数,
的导数, 是
是 的导数,若方程
的导数,若方程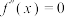 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”,同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心,若
的“拐点”,同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心,若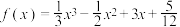 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 的对称中心为
的对称中心为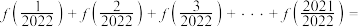
您最近一年使用:0次
2021-10-23更新
|
604次组卷
|
9卷引用:第1讲 函数的图象与性质(练 )-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)
(已下线)第1讲 函数的图象与性质(练 )-2022年高考数学二轮复习讲练测(新教材·新高考地区专用)江苏省徐州市第七中学2022-2023学年高三上学期12月学情检测数学试题北京市第一六一中学2022届高三10月月考数学试题江苏省淮安市高中校协作体2021-2022学年高三上学期期中联考数学试题(已下线)考向08 函数的奇偶性、周期性与对称性(重点)(已下线)第24讲 章末检测四-备战2023年高考数学一轮复习考点帮(新高考专用)江苏省盐城市大丰区新丰中学2022-2023学年高二上学期期末数学试题(已下线)宁夏石嘴山市第三中学2023-2024学年高二上学期期末数学试题(已下线)期末考试押题卷一(考试范围:苏教版2019选择性必修第一册)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
解题方法
4 . 对于三次函数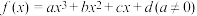 ,给出定义:设
,给出定义:设 是函数
是函数 的导数,
的导数, 是
是 的导数,若方程
的导数,若方程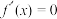 有实数解
有实数解 ,则称点
,则称点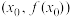 为函数
为函数 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若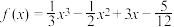 ,请你根据这一发现.
,请你根据这一发现.
(1)求函数 的对称中心;
的对称中心;
(2)计算 .
.
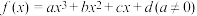 ,给出定义:设
,给出定义:设 是函数
是函数 的导数,
的导数, 是
是 的导数,若方程
的导数,若方程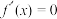 有实数解
有实数解 ,则称点
,则称点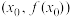 为函数
为函数 的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若
的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若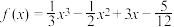 ,请你根据这一发现.
,请你根据这一发现.(1)求函数
 的对称中心;
的对称中心;(2)计算
 .
.
您最近一年使用:0次
解题方法
5 . 设函数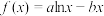 ,
,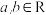 ,若曲线
,若曲线 在点(1,f(1))处的切线方程为
在点(1,f(1))处的切线方程为
(1)求a,b的值:
(2)若关于x的不等式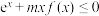 只有唯一实数解,求实数m的值.
只有唯一实数解,求实数m的值.
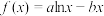 ,
,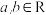 ,若曲线
,若曲线 在点(1,f(1))处的切线方程为
在点(1,f(1))处的切线方程为
(1)求a,b的值:
(2)若关于x的不等式
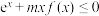 只有唯一实数解,求实数m的值.
只有唯一实数解,求实数m的值.
您最近一年使用:0次
6 . 已知函数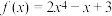 .
.
(1)求曲线 在点
在点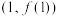 处的切线方程;
处的切线方程;
(2)若关于 的不等式
的不等式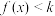 有实数解,求
有实数解,求 的取值范围.
的取值范围.
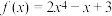 .
.(1)求曲线
 在点
在点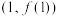 处的切线方程;
处的切线方程;(2)若关于
 的不等式
的不等式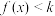 有实数解,求
有实数解,求 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
7 . 已知函数 .
.
(1)解关于x的不等式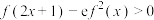 ;
;
(2)当 时,求函数
时,求函数 的最大值的取值范围.
的最大值的取值范围.
 .
.(1)解关于x的不等式
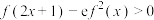 ;
;(2)当
 时,求函数
时,求函数 的最大值的取值范围.
的最大值的取值范围.
您最近一年使用:0次
解题方法
8 . 已知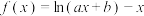 ,其中
,其中 ,
, .
.
(1)求 在
在 上为减函数的充要条件;
上为减函数的充要条件;
(2)求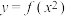 在
在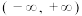 上的最大值;
上的最大值;
(3)解关于x的不等式: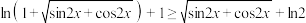 .
.
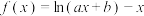 ,其中
,其中 ,
, .
.(1)求
 在
在 上为减函数的充要条件;
上为减函数的充要条件;(2)求
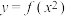 在
在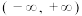 上的最大值;
上的最大值;(3)解关于x的不等式:
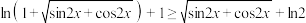 .
.
您最近一年使用:0次
2021·全国·模拟预测
解题方法
9 . 已知函数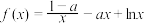 .
.
(1)当a=2时,求曲线f(x)在点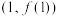 处的切线方程;
处的切线方程;
(2)若关于x的不等式 在[1,+∞)上有实数解,求实数a的取值范围.
在[1,+∞)上有实数解,求实数a的取值范围.
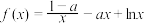 .
.(1)当a=2时,求曲线f(x)在点
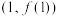 处的切线方程;
处的切线方程;(2)若关于x的不等式
 在[1,+∞)上有实数解,求实数a的取值范围.
在[1,+∞)上有实数解,求实数a的取值范围.
您最近一年使用:0次
21-22高二·全国·课后作业
10 . 观察实际情景,提出并分析问题
(1)实际情景
双十—就要到了,那时候大家都很忙,卖家搞促销,想赚更多的钱,买家想货比三家,买到物美价廉的商品,在这个交易过程中,快递不可或缺,你们有没有发现,商品都会被形形色色的盒子所包装,对于快递公司而言,包装同一个商品,用的材料越少越好,而给你一张硬纸片﹐制作出的盒子当然体积越大越好,这样制作非常环保.
(2)提出问题
一个边长为定值的正方形纸片按某种方式裁剪,做成一个无盖的方底纸盒,当盒底边长与高分别为多少时,盒子容积最大?最大容积是多少?
(3)分析问题
容积的计算依据裁剪的方法,由学生根据自己所学知识确定裁剪方法,确定剪裁方法后,我们可以通过长度关系,用未知数表示盒子容积,根据函数单调性求得容积最大时的相应的裁剪方法.
2.收集数据
现有一个面积为 平方厘米的正方形纸板
平方厘米的正方形纸板 .
.
3.剪裁过程
裁剪方案1:去除如阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得正方形的四个点重合于图中的点 ,正好形成一个长方体形状的包装盒.
,正好形成一个长方体形状的包装盒.
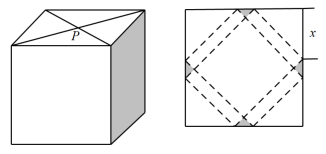
裁剪方案2:如图所示,先在正方形的相邻两个角各切去边长为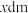 的正方形,然后在余下两角处各切去一个长、宽分别为
的正方形,然后在余下两角处各切去一个长、宽分别为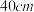 、
、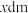 的矩形,再将剩余部分沿图中的虚线折起.
的矩形,再将剩余部分沿图中的虚线折起.
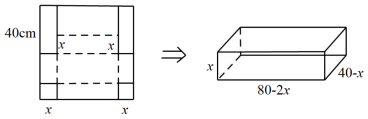
4.问题解决
裁剪方案1:设包装盒的高为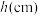 ,底面边长为
,底面边长为 ,
,
则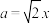 ,
,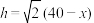 ,
,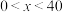 ,
,
所以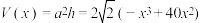 ,
,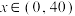 ;
;
可得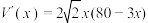 ,
,
当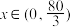 时,
时,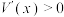 ;当
;当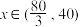 时,
时,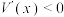 ,
,
所以函数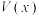 在
在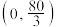 上递增,在
上递增,在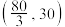 上递减,
上递减,
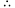 当
当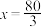 时,
时,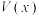 取得极大值也是最大值:
取得极大值也是最大值: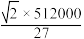 .
.
所以当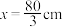 时,包装盒的容积最大是
时,包装盒的容积最大是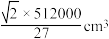 .
.
裁剪方案2:因为包装盒高 ,底面矩形的长为
,底面矩形的长为 ,宽为
,宽为 ,
,
所以包装盒的容积为 ,
,
函数的定义域为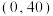 .
.
 ,
,
令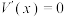 ,解得
,解得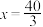 ,
,
∴当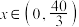 时,
时,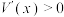 ,函数
,函数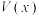 单调递增;
单调递增;
当 时,
时,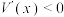 ,函数
,函数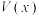 单调递减,
单调递减,
∴当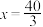 时,函数
时,函数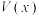 取得极大值,也是函数
取得极大值,也是函数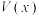 的最大值,
的最大值,
所以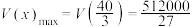
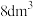 .
.
比较两种模型,故选择裁剪方案1.
5.检验模型
两种最值的计算都是依据给定的裁剪方法,可能会有其他的裁剪方法,求得的容积可能会更大.
6.延伸拓展
请同学们集思广益,研究一下是否有其他裁剪方法,并计算出相应的容积的最大值.
(1)实际情景
双十—就要到了,那时候大家都很忙,卖家搞促销,想赚更多的钱,买家想货比三家,买到物美价廉的商品,在这个交易过程中,快递不可或缺,你们有没有发现,商品都会被形形色色的盒子所包装,对于快递公司而言,包装同一个商品,用的材料越少越好,而给你一张硬纸片﹐制作出的盒子当然体积越大越好,这样制作非常环保.
(2)提出问题
一个边长为定值的正方形纸片按某种方式裁剪,做成一个无盖的方底纸盒,当盒底边长与高分别为多少时,盒子容积最大?最大容积是多少?
(3)分析问题
容积的计算依据裁剪的方法,由学生根据自己所学知识确定裁剪方法,确定剪裁方法后,我们可以通过长度关系,用未知数表示盒子容积,根据函数单调性求得容积最大时的相应的裁剪方法.
2.收集数据
现有一个面积为
 平方厘米的正方形纸板
平方厘米的正方形纸板 .
.3.剪裁过程
裁剪方案1:去除如阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得正方形的四个点重合于图中的点
 ,正好形成一个长方体形状的包装盒.
,正好形成一个长方体形状的包装盒.
裁剪方案2:如图所示,先在正方形的相邻两个角各切去边长为
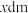 的正方形,然后在余下两角处各切去一个长、宽分别为
的正方形,然后在余下两角处各切去一个长、宽分别为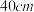 、
、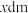 的矩形,再将剩余部分沿图中的虚线折起.
的矩形,再将剩余部分沿图中的虚线折起.
4.问题解决
裁剪方案1:设包装盒的高为
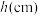 ,底面边长为
,底面边长为 ,
,则
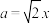 ,
,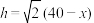 ,
,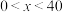 ,
,所以
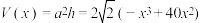 ,
,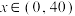 ;
;可得
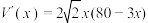 ,
,当
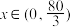 时,
时,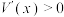 ;当
;当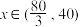 时,
时,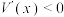 ,
,所以函数
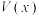 在
在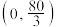 上递增,在
上递增,在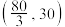 上递减,
上递减,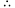 当
当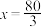 时,
时,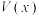 取得极大值也是最大值:
取得极大值也是最大值: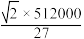 .
.所以当
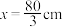 时,包装盒的容积最大是
时,包装盒的容积最大是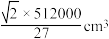 .
.裁剪方案2:因为包装盒高
 ,底面矩形的长为
,底面矩形的长为 ,宽为
,宽为 ,
,所以包装盒的容积为
 ,
,函数的定义域为
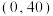 .
. ,
,令
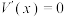 ,解得
,解得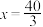 ,
,∴当
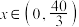 时,
时,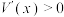 ,函数
,函数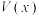 单调递增;
单调递增;当
 时,
时,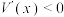 ,函数
,函数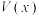 单调递减,
单调递减,∴当
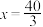 时,函数
时,函数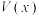 取得极大值,也是函数
取得极大值,也是函数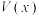 的最大值,
的最大值,所以
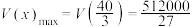
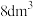 .
.比较两种模型,故选择裁剪方案1.
5.检验模型
两种最值的计算都是依据给定的裁剪方法,可能会有其他的裁剪方法,求得的容积可能会更大.
6.延伸拓展
请同学们集思广益,研究一下是否有其他裁剪方法,并计算出相应的容积的最大值.
您最近一年使用:0次



