名校
解题方法
1 . 已知函数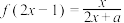
 .
.
(1)当 时,求出
时,求出 的解析式并用定义证明
的解析式并用定义证明 在
在 为单调递减;
为单调递减;
(2)若 在
在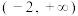 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
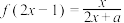
 .
.(1)当
 时,求出
时,求出 的解析式并用定义证明
的解析式并用定义证明 在
在 为单调递减;
为单调递减;(2)若
 在
在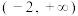 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
您最近一年使用:0次
10-11高三上·山东济南·阶段练习
名校
解题方法
2 . 已知函数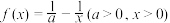 .
.
(1)求证: 在
在 上是单调递增函数;
上是单调递增函数;
(2)若 在
在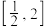 上的值域是
上的值域是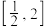 ,求a的值.
,求a的值.
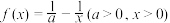 .
.(1)求证:
 在
在 上是单调递增函数;
上是单调递增函数;(2)若
 在
在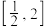 上的值域是
上的值域是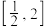 ,求a的值.
,求a的值.
您最近一年使用:0次
2020-10-30更新
|
1065次组卷
|
36卷引用:天津市咸水沽第一中学2022-2023学年高三上学期开学检测数学试题
天津市咸水沽第一中学2022-2023学年高三上学期开学检测数学试题(已下线)2011届山东省济南市第一中学高三10月阶段考试文科数学卷(已下线)2012-2013学年山东省临沂一中高一10月月考数学试卷(已下线)2012—2013学年福建省东山二中高一上学期第一次月考数学试卷(已下线)2014-2015学年广东省普宁市华美实验学校高一10月月考数学试卷江苏省泰州中学2017-2018学年高一10月月考数学试题四川省眉山第一中学2017-2018学年高一11月月考数学试题【校级联考】四川省凉山州2018-2019学年高一上学期期末检测数学试题新疆生产建设兵团农八师一四三团第一中学2018-2019学年高一上学期期末考试数学试题陕西省咸阳市武功县普集高中2019-2020学年高一上学期9月月考数学试题甘肃省武威市第十八中学2019年高三上学期10月月考数学试题宁夏石嘴山市平罗中学2019-2020学年高一上学期期中数学试题广东省佛山市实验中学2018-2019学年高一第二阶段测试数学试题安徽省安庆市怀宁中学2019-2020学年高一上学期第二次月考数学试题吉林省长春市十一高中、白城一中2017-2018学年高一上学期第一次月考联考数学试题广东省广州市第一一三中学2019-2020学年高一上学期期中数学试题甘肃省武威第十八中学2019-2020学年高三上学期第一次诊断考试数学试题(已下线)专题2.2 函数的单调性与最值(精测)-2021届高考数学(理)一轮复习讲练测(已下线)专题2.2 函数的单调性与最值(精练)-2021年高考数学(理)一轮复习学与练(已下线)专题2.2 函数的单调性与最值(精练)-2021年高考数学(文)一轮复习学与练宁夏银川市宁夏大学附属中学2019-2020学年高二下学期期末考试数学(文科)试卷(已下线)测试卷02 集合与函数概念(B)-2021届高考数学一轮复习(文理通用)单元过关测试卷(已下线)考点08 函数的单调性与最值(考点专练)-备战2021年新高考数学一轮复习考点微专题(已下线)测试卷01 集合与函数概念(A)-2021届高考数学一轮复习(文理通用)单元过关测试卷(已下线)专题03函数的单调性和最值-解题模板(已下线)专题03函数的单调性和最值解题模板A(已下线)【南昌新东方】江西省南昌十九中2020-2021学年高一上学期10月第一次月考数学试题陕西省延安市黄陵中学2020-2021学年高三(本部)上学期期中数学(理)试题广东省深圳市宝安区2019-2020学年高一上学期期末数学数学试题陕西省西安市阎良区关山中学2020-2021学年高一上学期12月月考数学试题河南省商丘市第一高级中学2021-2022学年高一上学期期中数学试题安徽省宿州市灵璧县渔沟中学2021-2022学年高一上学期第一次月考数学试题第二章 函数 综合测试卷-2022-2023学年高一上学期数学北师大版(2019)必修第一册北京名校2023届高三一轮总复习 第2章 函数与导数 2.4 函数的单调性陕西省渭南市集才中学老城分校2022届高三上学期期末数学(文)试题(已下线)第三章 函数及其应用3.2 函数的单调性
名校
解题方法
3 . 已知函数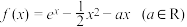 .
.
(1)若函数 在R上是增函数,求实数a的取值范围;
在R上是增函数,求实数a的取值范围;
(2)如果函数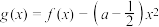 恰有两个不同的极值点
恰有两个不同的极值点 ,证明:
,证明: .
.
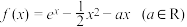 .
.(1)若函数
 在R上是增函数,求实数a的取值范围;
在R上是增函数,求实数a的取值范围;(2)如果函数
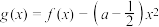 恰有两个不同的极值点
恰有两个不同的极值点 ,证明:
,证明: .
.
您最近一年使用:0次
2021-09-13更新
|
2109次组卷
|
13卷引用:天津市第一中学2019-2020学年高二下学期期末数学试题
天津市第一中学2019-2020学年高二下学期期末数学试题(已下线)极值点偏移专题06含指数式的极值点偏移问题山东省师范大学附属中学2021-2022学年高三上学期开学考试数学试题炎德英才联考合作体2021-2022学年高三上学期10月联考数学试题湖南省长沙市长郡中学2021-2022学年高三上学期10月月考数学试题湖南省名校联合体2021-2022学年高三上学期10月联考数学试题河北省石家庄市第一中学2022届高三上学期第二次学情反馈数学试题江西省景德镇市第一中学2021-2022学年高二(2班)上学期期中数学试题甘肃省张掖市某重点校2022-2023学年高三上学期第三次检测数学试题甘肃省敦煌中学2022-2023学年高三上学期第二次诊断考试数学理科试题安徽省滁州市定远县民族中学2021-2022学年高三下学期3月月考数学(文)试题浙江省宁波市2022-2023学年高二下学期期末数学试题(A)(已下线)第三章 重点专攻二 不等式的证明问题(讲)
名校
4 . 已知函数 的定义域为
的定义域为 ,且对任意的
,且对任意的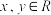 有
有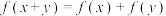 . 当
. 当 时,
时, ,
,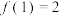 .
.
(1)求 并证明
并证明 的奇偶性;
的奇偶性;
(2)判断 的单调性并证明;
的单调性并证明;
(3)求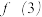 ;若
;若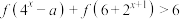 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,且对任意的
,且对任意的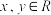 有
有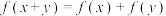 . 当
. 当 时,
时, ,
,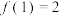 .
.(1)求
 并证明
并证明 的奇偶性;
的奇偶性;(2)判断
 的单调性并证明;
的单调性并证明;(3)求
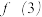 ;若
;若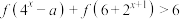 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2019-02-14更新
|
2237次组卷
|
6卷引用:【校级联考】天津市六校(静海一中、宝坻一中、杨村一中等)2018-2019学年高一上学期期末考试数学试题
名校
5 . 已知f(x)=log4(4x+1)+kx是偶函数.
(1)求k的值;
(2)判断函数y=f(x)- x在R上的单调性,并加以证明;
x在R上的单调性,并加以证明;
(3)设g(x)=log4(a•2x-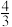 a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
(1)求k的值;
(2)判断函数y=f(x)-
 x在R上的单调性,并加以证明;
x在R上的单调性,并加以证明;(3)设g(x)=log4(a•2x-
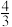 a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且仅有一个交点,求实数a的取值范围.
您最近一年使用:0次
2019-01-12更新
|
745次组卷
|
2卷引用:【区级联考】天津市南开区2018-2019学年高一(上)期中数学试题
名校
解题方法
6 . 已知二次函数
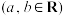 ,
,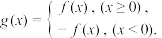
(1)若 ,且对
,且对 ,函数
,函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;
(2)在(1)的条件下,函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(3)设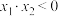 ,
,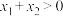 ,
, 且
且 为偶函数,证明
为偶函数,证明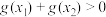

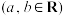 ,
,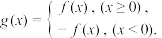
(1)若
 ,且对
,且对 ,函数
,函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式;(2)在(1)的条件下,函数
 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;(3)设
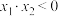 ,
,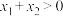 ,
, 且
且 为偶函数,证明
为偶函数,证明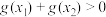
您最近一年使用:0次
名校
7 . 已知函数 是奇函数,且
是奇函数,且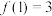 ,其中
,其中 .
.
(1)求 和
和 的值;
的值;
(2)判断 在
在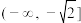 上的单调性,并加以证明.
上的单调性,并加以证明.
 是奇函数,且
是奇函数,且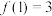 ,其中
,其中 .
.(1)求
 和
和 的值;
的值;(2)判断
 在
在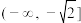 上的单调性,并加以证明.
上的单调性,并加以证明.
您最近一年使用:0次
名校
8 . 函数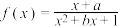 是定义在
是定义在 上的奇函数.
上的奇函数.
⑴确定函数 的解析式;
的解析式;
⑵用定义证明 的单调性;
的单调性;
⑶解不等式
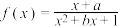 是定义在
是定义在 上的奇函数.
上的奇函数.⑴确定函数
 的解析式;
的解析式;⑵用定义证明
 的单调性;
的单调性;⑶解不等式

您最近一年使用:0次
2018-11-18更新
|
319次组卷
|
3卷引用:【全国百强校】天津市实验中学2018-2019学年度高一上学期期中数学试题
9 . 设 是实数,已知奇函数
是实数,已知奇函数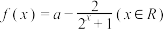 ,
,
(1)求 的值;
的值;
(2)证明函数 在R上是增函数;
在R上是增函数;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0有解,求k的取值范围.
 是实数,已知奇函数
是实数,已知奇函数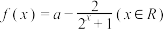 ,
,(1)求
 的值;
的值;(2)证明函数
 在R上是增函数;
在R上是增函数;(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0有解,求k的取值范围.
您最近一年使用:0次
2018-12-02更新
|
1440次组卷
|
2卷引用:【校级联考】天津市宝坻区普通高中2018-2019学年高一上学期三校联考数学试题
名校
10 . 已知 是定义在
是定义在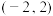 上的减函数,且
上的减函数,且 ,满足对任意
,满足对任意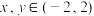 ,都有
,都有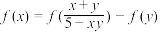 .
.
(1)求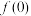 的值;
的值;
(2)判断 的奇偶性并证明;
的奇偶性并证明;
(3)解不等式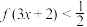 .
.
 是定义在
是定义在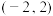 上的减函数,且
上的减函数,且 ,满足对任意
,满足对任意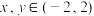 ,都有
,都有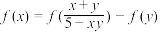 .
.(1)求
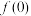 的值;
的值;(2)判断
 的奇偶性并证明;
的奇偶性并证明;(3)解不等式
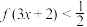 .
.
您最近一年使用:0次



