名校
1 . 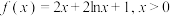
(1)证明: 存在唯一的零点
存在唯一的零点 ,且
,且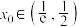
(2)若 的零点记为
的零点记为 ,设
,设 ,求证
,求证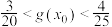
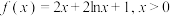
(1)证明:
 存在唯一的零点
存在唯一的零点 ,且
,且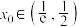
(2)若
 的零点记为
的零点记为 ,设
,设 ,求证
,求证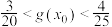
您最近一年使用:0次
2023-10-01更新
|
184次组卷
|
3卷引用:福建省漳州实验高级中学2022-2023学年高一创新班上学期期中考试数学试题
福建省漳州实验高级中学2022-2023学年高一创新班上学期期中考试数学试题福建省厦门市厦门二中2023-2024学年高一上学期12月月考数学试题(已下线)专题04 指数函数与对数函数2-2024年高一数学寒假作业单元合订本
名校
2 . 设 ,函数
,函数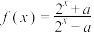 .
.
(1)若 ,求证:函数
,求证:函数 为奇函数;
为奇函数;
(2)若 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;
(3)若 ,函数
,函数 在区间
在区间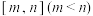 上的取值范围是
上的取值范围是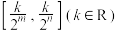 ,求
,求 的范围.
的范围.
 ,函数
,函数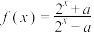 .
.(1)若
 ,求证:函数
,求证:函数 为奇函数;
为奇函数;(2)若
 ,判断并证明函数
,判断并证明函数 的单调性;
的单调性;(3)若
 ,函数
,函数 在区间
在区间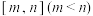 上的取值范围是
上的取值范围是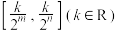 ,求
,求 的范围.
的范围.
您最近一年使用:0次
2023-03-14更新
|
687次组卷
|
3卷引用:福建省漳州市第三中学2022-2023学年高一上学期期中数学试题
名校
解题方法
3 . (1)平面多边形中,三角形具有稳定性,而四边形不具有这一性质.四边形ABCD的顶点在同一平面上,已知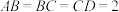 ,
,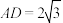 .当BD长度变化时,
.当BD长度变化时, 是否为一个定值?若是,求出这个定值;若否,说明理由.
是否为一个定值?若是,求出这个定值;若否,说明理由.
(2)在平面四边形ABCD中,已知 ,
,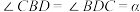 ,
, .若
.若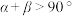 ,求证:
,求证: .
.
(3)记 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知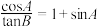 ,求
,求 的取值范围.
的取值范围.
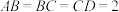 ,
,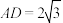 .当BD长度变化时,
.当BD长度变化时, 是否为一个定值?若是,求出这个定值;若否,说明理由.
是否为一个定值?若是,求出这个定值;若否,说明理由.(2)在平面四边形ABCD中,已知
 ,
,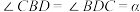 ,
, .若
.若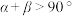 ,求证:
,求证: .
.(3)记
 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知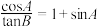 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
4 . 若函数 与区间
与区间 同时满足:①区间
同时满足:①区间 为
为 的定义域的子集,②对任意
的定义域的子集,②对任意 ,存在常数
,存在常数 ,使得
,使得 成立,则称
成立,则称 是区间
是区间 上的有界函数,其中
上的有界函数,其中 称为
称为 的一个上界.(注:涉及复合函数单调性求最值可直接使用单调性,不需要证明)
的一个上界.(注:涉及复合函数单调性求最值可直接使用单调性,不需要证明)
(1)试判断函数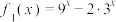 ,
, 是否为
是否为 上的有界函数?并说明理由.
上的有界函数?并说明理由.
(2)已知函数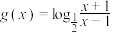 是区间
是区间 上的有界函数,设
上的有界函数,设 在区间
在区间 上的上界为
上的上界为 ,求
,求 的取值范围;
的取值范围;
(3)若函数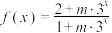 ,问:
,问: 在区间
在区间 上是否存在上界
上是否存在上界 ?若存在,求出
?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 与区间
与区间 同时满足:①区间
同时满足:①区间 为
为 的定义域的子集,②对任意
的定义域的子集,②对任意 ,存在常数
,存在常数 ,使得
,使得 成立,则称
成立,则称 是区间
是区间 上的有界函数,其中
上的有界函数,其中 称为
称为 的一个上界.(注:涉及复合函数单调性求最值可直接使用单调性,不需要证明)
的一个上界.(注:涉及复合函数单调性求最值可直接使用单调性,不需要证明)(1)试判断函数
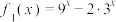 ,
, 是否为
是否为 上的有界函数?并说明理由.
上的有界函数?并说明理由.(2)已知函数
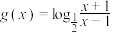 是区间
是区间 上的有界函数,设
上的有界函数,设 在区间
在区间 上的上界为
上的上界为 ,求
,求 的取值范围;
的取值范围;(3)若函数
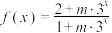 ,问:
,问: 在区间
在区间 上是否存在上界
上是否存在上界 ?若存在,求出
?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
5 . 对于定义域为 的函数
的函数 ,如果存在区间
,如果存在区间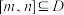 .同时满足:①
.同时满足:① 在
在 内是单调函数;②当定义域是
内是单调函数;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“优美区间”.
是该函数的“优美区间”.
(1)求证: ,
, 是函数
是函数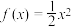 的一个“优美区间”;
的一个“优美区间”;
(2)函数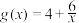 是否存在“优美区间”?若存在,求出它的“优美区间”,若不存在,请说明理由.
是否存在“优美区间”?若存在,求出它的“优美区间”,若不存在,请说明理由.
(3)已知函数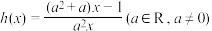 有“优美区间”
有“优美区间” ,当
,当 变化时,求出
变化时,求出 的最大值.
的最大值.
 的函数
的函数 ,如果存在区间
,如果存在区间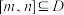 .同时满足:①
.同时满足:① 在
在 内是单调函数;②当定义域是
内是单调函数;②当定义域是 时,
时, 的值域也是
的值域也是 ,则称
,则称 是该函数的“优美区间”.
是该函数的“优美区间”.(1)求证:
 ,
, 是函数
是函数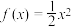 的一个“优美区间”;
的一个“优美区间”;(2)函数
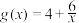 是否存在“优美区间”?若存在,求出它的“优美区间”,若不存在,请说明理由.
是否存在“优美区间”?若存在,求出它的“优美区间”,若不存在,请说明理由.(3)已知函数
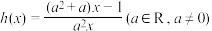 有“优美区间”
有“优美区间” ,当
,当 变化时,求出
变化时,求出 的最大值.
的最大值.
您最近一年使用:0次
2022-11-28更新
|
477次组卷
|
3卷引用:福建省福州市仓山区福建师大附中2023-2024学年高一上学期期中数学试题
福建省福州市仓山区福建师大附中2023-2024学年高一上学期期中数学试题江苏省南京市雨花台中学2022-2023学年高一上学期期中数学试题(已下线)全册综合测试卷(提高篇)-2022-2023学年高一数学举一反三系列(人教A版2019必修第一册)
名校
解题方法
6 . 已知函数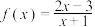 .
.
(1)用函数单调性的定义证明: 在
在 上是增函数;
上是增函数;
(2)求函数 在区间
在区间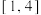 上的值域.
上的值域.
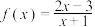 .
.(1)用函数单调性的定义证明:
 在
在 上是增函数;
上是增函数;(2)求函数
 在区间
在区间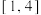 上的值域.
上的值域.
您最近一年使用:0次
2023-11-02更新
|
1389次组卷
|
5卷引用:福建省泉州市泉州科技中学2023-2024学年高一上学期期中数学试题
福建省泉州市泉州科技中学2023-2024学年高一上学期期中数学试题北京市交通大学附属中学2023-2024学年高一上学期期中考试数学试题北京市海淀区北京交通大学附属中学2023-2024学年高一上学期期中练习数学试题(已下线)第三章 函数的概念与性质【单元基础卷】-【满分全攻略】(人教A版2019必修第一册)(已下线)专题01 函数的单调性证明考点(期末大题1)-期末题型秒杀技巧及专项练习(人教A版2019必修第一册)
解题方法
7 . 已知函数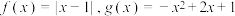 .
.
(1)在同一坐标系中画出函数 ,
, 的图象;
的图象;
(2)定义:对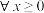 ,
, 表示
表示 与
与 中的较小者,记为
中的较小者,记为 ,分别用函数图象法和解析法表示函数
,分别用函数图象法和解析法表示函数 ,并写出
,并写出 的单调区间和值域(不需要证明).
的单调区间和值域(不需要证明).
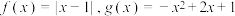 .
.

(1)在同一坐标系中画出函数
 ,
, 的图象;
的图象;(2)定义:对
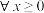 ,
, 表示
表示 与
与 中的较小者,记为
中的较小者,记为 ,分别用函数图象法和解析法表示函数
,分别用函数图象法和解析法表示函数 ,并写出
,并写出 的单调区间和值域(不需要证明).
的单调区间和值域(不需要证明).
您最近一年使用:0次
名校
解题方法
8 . 已知函数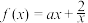 ,且
,且 .
.
(1)求 的值,并证明:
的值,并证明: 在区间
在区间 上单调递减;
上单调递减;
(2)若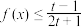 对
对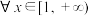 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
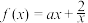 ,且
,且 .
.(1)求
 的值,并证明:
的值,并证明: 在区间
在区间 上单调递减;
上单调递减;(2)若
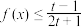 对
对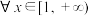 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
9 . 已知函数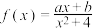 是定义在
是定义在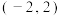 上的奇函数,且
上的奇函数,且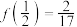 .
.
(1)求a,b的值,并用定义证明:函数 在区间
在区间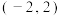 上的单调性;
上的单调性;
(2)若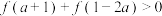 ,求实数a的取值范围;
,求实数a的取值范围;
(3)写出函数 的值域(不必写出解答过程)
的值域(不必写出解答过程)
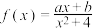 是定义在
是定义在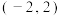 上的奇函数,且
上的奇函数,且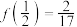 .
.(1)求a,b的值,并用定义证明:函数
 在区间
在区间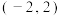 上的单调性;
上的单调性;(2)若
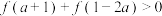 ,求实数a的取值范围;
,求实数a的取值范围;(3)写出函数
 的值域(不必写出解答过程)
的值域(不必写出解答过程)
您最近一年使用:0次
名校
10 . 已知函数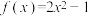
(1)用定义证明 是偶函数;
是偶函数;
(2)用定义证明 在
在 上是减函数;
上是减函数;
(3)作出函数 的图象,并写出函数
的图象,并写出函数 当
当 时的最大值与最小值.
时的最大值与最小值.
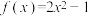
(1)用定义证明
 是偶函数;
是偶函数;(2)用定义证明
 在
在 上是减函数;
上是减函数;(3)作出函数
 的图象,并写出函数
的图象,并写出函数 当
当 时的最大值与最小值.
时的最大值与最小值.
您最近一年使用:0次



