名校
解题方法
1 . 对于函数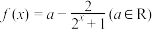 .
.
(1)探索函数 的单调性并用定义证明;
的单调性并用定义证明;
(2)是否存在实数a使函数 为奇函数?
为奇函数?
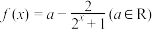 .
.(1)探索函数
 的单调性并用定义证明;
的单调性并用定义证明;(2)是否存在实数a使函数
 为奇函数?
为奇函数?
您最近一年使用:0次
2 . 固定项链的两端,在重力的作用下项链所形成的曲线是悬链线.1691年,莱布尼茨等得出“悬链线”方程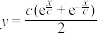 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数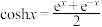 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数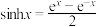 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.
(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论: _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);
(2)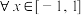 ,不等式
,不等式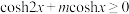 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若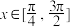 ,试比较
,试比较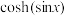 与
与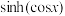 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
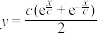 ,其中
,其中 为参数.当
为参数.当 时,就是双曲余弦函数
时,就是双曲余弦函数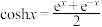 ,类似地我们可以定义双曲正弦函数
,类似地我们可以定义双曲正弦函数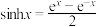 .它们与正、余弦函数有许多类似的性质.
.它们与正、余弦函数有许多类似的性质.(1)类比正弦函数的二倍角公式,请写出双曲正弦函数的一个正确的结论:
 _____________.(只写出即可,不要求证明);
_____________.(只写出即可,不要求证明);(2)
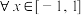 ,不等式
,不等式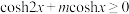 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
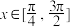 ,试比较
,试比较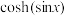 与
与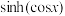 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
2024-01-27更新
|
1513次组卷
|
14卷引用:云南省昆明市云南师范大学附属中学2023-2024学年高一下学期期末数学模拟测试试题(一)
云南省昆明市云南师范大学附属中学2023-2024学年高一下学期期末数学模拟测试试题(一)福建省宁德市2023-2024学年高一上学期1月期末质量检测数学试题(已下线)专题04 三角函数恒等变形综合大题归类 -期末考点大串讲(苏教版(2019))(已下线)专题08 期末必刷解答题专题训练的7种常考题型归类-期末真题分类汇编(北师大版2019必修第二册)重庆市缙云教育联盟2024届高三下学期2月月度质量检测数学试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)讲河南省名校联盟2023-2024学年高一下学期3月测试数学试题(已下线)第八章:向量的数量积与三角恒等变换章末重点题型复习(2)-同步精品课堂(人教B版2019必修第三册)河南省信阳市信阳高级中学2023-2024学年高一下学期3月月考(一)数学试题(已下线)第8章:向量的数量积与三角恒等变换章末综合检测卷(新题型)-【帮课堂】(人教B版2019必修第三册)江西省上饶市横峰县横峰中学2023-2024学年高一下学期期中考试数学试卷(已下线)拔高点突破05 函数与导数背景下的新定义压轴解答题(九大题型)(已下线)拔高点突破01 三角函数与解三角形背景下的新定义问题(十大题型)(已下线)专题2 函数与导数新定义压轴大题(一)【讲】
名校
解题方法
3 . 下列函数中,在区间 上为增函数的是( )
上为增函数的是( )
 上为增函数的是( )
上为增函数的是( )A.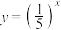 | B.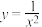 |
C.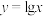 | D. |
您最近一年使用:0次
2023-12-09更新
|
256次组卷
|
11卷引用:云南省曲靖市马龙区第一中学2023-2024学年高一上学期期末考试数学试题
云南省曲靖市马龙区第一中学2023-2024学年高一上学期期末考试数学试题云南省昭通市威信县第二中学2023-2024学年高一下学期期末考试数学试题青海省海西蒙古族藏族自治州格尔木市2023-2024学年高一下学期全市教学质量检测(期末)考试数学试题内蒙古集宁新世纪中学2023-2024学年高一上学期期末数学试卷甘肃省陇南市第一中学2023-2024学年高一下学期期末考试数学试题云南省曲靖市富源县第八中学2023-2024学年高一下学期5月月考数学试卷甘肃定西市临洮县文峰中学2023-2024学年高一下学期期末质量检测(一)数学试题黑龙江省齐齐哈尔市克东县第一中学2023-2024学年高一上学期12月月考数学试卷贵州省铜仁市第八中学2023-2024学年高一上学期12月月考数学试题青海省海东市民和回族土族自治县城西高级中学2023-2024学年高一下学期6月月考数学试题河南省安阳市林州市第一中学2024-2025学年高二上学期8月月考数学试题
名校
解题方法
4 . 已知指数函数 的图象经过点
的图象经过点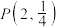 .
.
(1)求函数 的解析式并判断
的解析式并判断 的单调性;
的单调性;
(2)若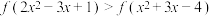 ,求
,求 的取值范围.
的取值范围.
 的图象经过点
的图象经过点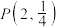 .
.(1)求函数
 的解析式并判断
的解析式并判断 的单调性;
的单调性;(2)若
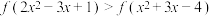 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-20更新
|
413次组卷
|
2卷引用:云南省昆明市西南联大研究院附中2021-2022学年高一上学期期末数学试题
5 . 下列函数中,在定义域上为减函数的是( )
A. | B.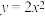 |
C.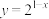 | D.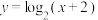 |
您最近一年使用:0次
6 . 下列函数中,在定义域上单调递增的是( )
A. | B.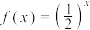 | C. | D.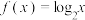 |
您最近一年使用:0次
2023-05-20更新
|
1018次组卷
|
4卷引用:云南省(新教材)2021-2022学年高一春季学期期末普通高中学业水平考试数学试题
名校
7 . 函数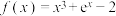 ,若
,若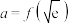 ,
,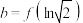 ,
,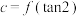 ,则( )
,则( )
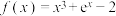 ,若
,若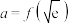 ,
,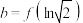 ,
,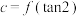 ,则( )
,则( )A.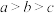 | B.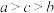 |
C.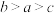 | D.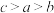 |
您最近一年使用:0次
2023-03-31更新
|
646次组卷
|
4卷引用:云南省昆明市西山区2022-2023学年高一上学期2月期末考试数学试题
云南省昆明市西山区2022-2023学年高一上学期2月期末考试数学试题河北省石家庄市河北正中实验中学2022-2023学年高二下学期月考三数学试题河北省衡水市第二中学2022-2023学年高一下学期期中数学试题(已下线)第六章 导数与不等式恒成立问题 专题一 两类经典不等式 微点1 三个重要的指数不等式
名校
解题方法
8 . 已知偶函数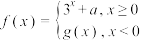 ,则满足
,则满足 的实数
的实数 的取值范围是( )
的取值范围是( )
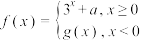 ,则满足
,则满足 的实数
的实数 的取值范围是( )
的取值范围是( )A. | B. | C.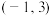 | D.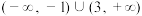 |
您最近一年使用:0次
2022-12-26更新
|
813次组卷
|
4卷引用:云南省昆明市第三中学2022届高三上学期期末考试数学(理)试题
解题方法
9 . 已知函数 ,
,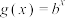 ,若
,若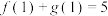 ,
,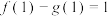 .
.
(1)求 ,
, 的解析式;
的解析式;
(2)若 ,试比较m,n的大小.
,试比较m,n的大小.
 ,
,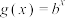 ,若
,若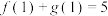 ,
,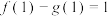 .
.(1)求
 ,
, 的解析式;
的解析式;(2)若
 ,试比较m,n的大小.
,试比较m,n的大小.
您最近一年使用:0次
2022-07-09更新
|
1112次组卷
|
4卷引用:云南省昆明市2021-2022学年高一下学期期末质量检测数学试题
名校
解题方法
10 . 设函数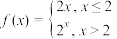 ,若
,若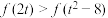 ,则t的取值范围是
,则t的取值范围是___________ .
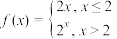 ,若
,若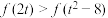 ,则t的取值范围是
,则t的取值范围是
您最近一年使用:0次
2022-02-25更新
|
1006次组卷
|
3卷引用:云南省昆明市第一中学2021-2022学年高一上学期期末考试数学试题
云南省昆明市第一中学2021-2022学年高一上学期期末考试数学试题(已下线)技巧05 第二篇 解题技巧(测试卷)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》湖南省永州市第二十八中学2021-2022学年高一下学期期中数学试题



