1 . 朱世杰是元代著名数学家,他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题,主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔,小明模仿“堆垛”问题,将它们全部堆放成纵断面为等腰梯形的“垛”,要求层数不小于2,且从最下面一层开始,每一层比上一层多1根,则该“等腰梯形垛”应堆放的层数可以是( )
| A.4 | B.5 | C.7 | D.8 |
您最近一年使用:0次
2023-01-03更新
|
873次组卷
|
15卷引用:新疆维吾尔自治区昌吉市第一中学2023-2024学年高二上学期12月月考数学试题
新疆维吾尔自治区昌吉市第一中学2023-2024学年高二上学期12月月考数学试题湖南省、河北省新高考联考2020-2021学年高三上学期10月质量检测数学试题湖北省鄂州高中2020-2021学年高三上学期10月质量检测数学试题甘肃省临洮中学2022-2023学年高二上学期第一次月考数学试题新疆乌鲁木齐八一中学2022-2023学年高二上学期期末考试数学试题湖北省十堰市普通高中协作体2022-2023学年高二下学期3月月考数学试题湖南省益阳市桃江县第一中学2020-2021学年高二下学期入学考试数学试题(已下线)突破4.2.2 等差数列的前n项和课时训练-【新教材优创】突破满分数学之2020-2021学年高二数学课时训练(人教A版2019选择性必修第二册) 人教A版(2019) 选修第二册 突围者 第四章 第二节 课时2 等差数列的前n项和公式(1)苏教版(2019) 选修第一册 选填专练 第4章 限时小练26 等差数列的前n项和(1)人教A版(2019) 选修第二册 实战演练 第四章 数列 课时练习05 等差数列的前n项和公式(2)湖北省荆州中学2022-2023学年高二上学期期末数学试题辽宁省沈阳市东北育才学校2020-2021学年上学期高三期末考试数学试题(已下线)专题29 等差数列通项与前n项和(已下线)4.2.2 等差数列的前n项和公式——课堂例题
2 . 记 为数列
为数列 的前n项和,已知
的前n项和,已知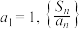 是公差为
是公差为 的等差数列.
的等差数列.
(1)求 的通项公式;
的通项公式;
(2)证明: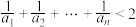 .
.
 为数列
为数列 的前n项和,已知
的前n项和,已知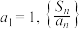 是公差为
是公差为 的等差数列.
的等差数列.(1)求
 的通项公式;
的通项公式;(2)证明:
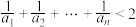 .
.
您最近一年使用:0次
2022-06-07更新
|
96764次组卷
|
101卷引用:新疆乌鲁木齐市第七十中学2024届高三上学期第二次月考数学试题
新疆乌鲁木齐市第七十中学2024届高三上学期第二次月考数学试题广东省佛山市南海区九江中学2021-2022学年高二下学期6月校内三检数学试题辽宁省营口市第二高级中学2021-2022学年高二下学期6月月考数学试题吉林省白山市抚松县第一中学2022-2023学年高三上学期第三次校内模拟数学试题四川省遂宁中学校2022-2023学年高二下学期3月月考数学(理)试题陕西省汉中市西乡县第一中学2023届高三上学期第一次检测理科数学试题贵州省黔西南州兴义市第六中学2022-2023学年高二下学期第三次月考数学试题河南省鹤壁市高中2022-2023学年高二下学期第五次段考数学试题广东省惠州市龙门县高级中学2024届高三上学期10月月考数学试题湖南省邵阳市邵东创新实验学校2023-2024学年高三上学期第三次月考数学试题河南省光山县第二高级中学2023-2024学年高三上学期11月阶段测试数学试题甘肃省白银市会宁县第四中学2024届高三上学期第三次月考数学试题江苏省江阴市第一中学2024届高三上学期12月阶段测试数学试题河南省开封市五县2023-2024学年高二上学期联考数学试题江苏省连云港市赣马高级中学2024届高三上学期12月学情检测数学试题云南省宣威市第三中学2023-2024学年高二下学期第一次月考数学试题河南省焦作市第一中学2024届高三上学期11月月考数学试题上海市青浦高级中学2024-2025学年高三上学期9月考试数学试卷江苏省南通市启东中学2023-2024学年高二上学期10月考试数学试题江苏省苏州三中2024-2025学年高二上学期10月月考数学试题湖南省邵阳市邵东市第一中学2024-2025学年高三上学期第三次月考(10月)数学试题安徽省安庆市怀宁县第二中学2025届高三上学期第二次月考数学试卷2022年新高考全国I卷数学真题(已下线)2022年全国新高考Ⅰ卷数学试题变式题9-12题(已下线)第5讲 数列与不等式(已下线)第04讲 数列求和 (讲)-2023年高考数学一轮复习讲练测(新教材新高考)(已下线)专题22 常见数列的通项求法-2023届高考数学一轮复习精讲精练(新高考专用)(已下线)专题06 数列解答题(已下线)专题05 数列解答题(已下线)专题26 数列的通项公式-1(已下线)专题27 数列求和-2(已下线)专题24 等差数列及其前n项和-3黑龙江省七台河市勃利县高级中学2022-2023学年高三上学期开学考试数学试题(已下线)第02讲 等差数列及前n项和(练)(已下线)第04讲 数列求和(练)(已下线)2022年全国新高考Ⅰ卷数学试题变式题17-19题(已下线)考向19等差数列及其前n项和(重点) - 1(已下线)专题6-1 数列递推与通项公式22种归类-3(已下线)专题5 2022年高考“数列”专题命题分析(已下线)专题1 2022高考命题分析与专家整体解读(已下线)专题05 数列放缩(精讲精练)-1第四章 数列(单元测)西藏拉萨中学2022-2023学年高二上学期期末考试数学试题(已下线)专题5 数列 第2讲 数列通项与求和(已下线)专题3 解答题题型(已下线)重组卷01(已下线)押新高考第18题 数列综合(已下线)第7讲 数列求和9种常见题型总结 (2)(已下线)专题15 数列求和-3(已下线)拓展五:近五年数列高考真题分类汇编(2)专题05数列(成品)专题05数列(添加试题分类成品)(已下线)专题07 数列-1(已下线)重难专攻(五) 数列中的综合问题 A素养养成卷(已下线)第一节 数列的概念与表示(核心考点集训)甘肃省天水市等2地2023届高三上学期期末理科数学试题(已下线)第1讲 数与式的运算【讲】第一章 必须掌握的计算基础(已下线)第04讲 数列的通项公式(练习)-24.2.2 等差数列的前n项和公式练习人教A版(2019) 选修第二册 数学奇书 第四章 数列 4.2等差数列 4.2.2 等差数列的前n项和公式 第2课时 等差数列前n项和的综合应用安徽省滁州市滁州中学2023-2024学年高二上学期期末数学试题宁夏回族自治区银川一中2023-2024学年高二上学期期末考试数学试题(已下线)考点12 数列中的不等关系 2024届高考数学考点总动员【练】(已下线)专题04 数列(3)(已下线)大招10裂项相消法(已下线)艺体生一轮复习 第六章 数列 第29讲 数列求和的方法【讲】(已下线)艺体生一轮复习 第六章 数列 第28讲 数列通项的求法【讲】专题04数列求和(裂项求和)(已下线)第3讲:数列中的不等问题【练】(已下线)第4讲:数列中的最值问题【练】(已下线)专题04 数列及求和(讲义)(已下线)重难点03:数列近3年高考真题赏析-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)重难点02:求数列前n项和常用10种解题策略-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)专题10 数列不等式的放缩问题 (7大核心考点)(讲义)(已下线)专题05 数列 第三讲 数列与不等关系(解密讲义)(已下线)专题05 数列 第二讲 数列的求和(解密讲义)(已下线)专题05 数列 第一讲 数列的递推关系(分层练)(已下线)专题05 数列 第一讲 数列的递推关系(解密讲义)(已下线)专题6.1 等差数列及其前n项和【九大题型】(已下线)专题06:数列大题真题精练(已下线)专题09 数列的通项公式、数列求和及综合应用(练习)-2(已下线)第17题 数列不等式变化多端,求和灵活证明方法多(优质好题一题多解)广东省珠海市六校2023-2024学年高二下学期4月期中考试数学试题(已下线)5.1 数列的概念及其表示(高考真题素材之十年高考)(已下线)专题21 数列解答题(理科)-3(已下线)专题21 数列解答题(文科)-2(已下线)专题2 考前押题大猜想6-10(已下线)模块三 失分陷阱4 模块融合题找不准解题方法专题06数列四川省泸州市龙马潭区2023-2024学年高二下学期5月期中考试数学试题(已下线)五年新高考专题06数列(已下线)三年新高考专题06数列(已下线)暑假作业02 数列通项公式的构造及其数列求和-【暑假分层作业】(人教A版2019)(已下线)第05讲 数列求和(九大题型)(练习)四川省成都市天府新区太平中学2024届高三数学文科模拟测试(三)(已下线)专题13 数列(4大考向真题解读)-备战2025年高考数学真题题源解密(新高考卷)(已下线)第04讲 数列的通项公式(十八大题型)(练习)-2江苏省南京市宁海中学2023-2024学年高二上学期期末考试数学试题【巩固卷】第1章数列 高考强化单元测试B-湘教版(2019)选择性必修第一册湖南省邵阳市海谊中学2024届高三上学期期末考试数学试题江苏省镇江中学2024-2025学年高二上学期期初学情检测数学试题
名校
解题方法
3 . 已知公差为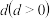 的等差数列
的等差数列 中,
中,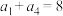 ,
,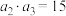 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,令
,令 ,求数列
,求数列 的前n项和
的前n项和 .
.
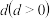 的等差数列
的等差数列 中,
中,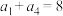 ,
,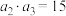 .
.(1)求数列
 的通项公式;
的通项公式;(2)若
 ,令
,令 ,求数列
,求数列 的前n项和
的前n项和 .
.
您最近一年使用:0次
2022-01-22更新
|
344次组卷
|
2卷引用:新疆喀什地区莎车县第一中学2023届高三上学期11月月考理科数学试题
4 . 设等差数列 前
前 项和为
项和为 ,等差数列
,等差数列 前
前 项和为
项和为 ,若
,若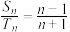 .则
.则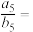 ( )
( )
 前
前 项和为
项和为 ,等差数列
,等差数列 前
前 项和为
项和为 ,若
,若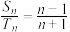 .则
.则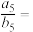 ( )
( )A. | B. | C. | D.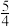 |
您最近一年使用:0次
2021-01-28更新
|
4645次组卷
|
6卷引用:新疆兵团第三师图木舒克市鸿德实验学校2022-2023学年高二下学期第一次月考数学试题
新疆兵团第三师图木舒克市鸿德实验学校2022-2023学年高二下学期第一次月考数学试题江西省抚州市部分中学联合体2020-2021学年高一下学期第一次月考数学试题陕西省宝鸡市渭滨区2020-2021学年高二上学期期末数学(文)试题陕西省宝鸡市渭滨区2020-2021学年高二上学期期末数学(理)试题(已下线)第四章 数列(基础测评卷)-2020-2021学年高二数学单元复习(人教A版2019选择性必修第二册)(已下线)专题1.3 数列 章末检测3(难)-【满分计划】2021-2022学年高二数学阶段性复习测试卷(人教A版2019选择性必修第二册)
名校
解题方法
5 . 已知数列 满足:
满足: ,
,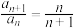 数列
数列 是等比数列,并满足
是等比数列,并满足 ,且
,且 ,
,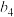 ,
, 成等差数列.
成等差数列.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若数列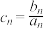 ,求数列
,求数列 的前
的前 项和
项和 .
.
 满足:
满足: ,
, 数列
数列 是等比数列,并满足
是等比数列,并满足 ,且
,且 ,
,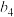 ,
, 成等差数列.
成等差数列.(1)求数列
 ,
, 的通项公式;
的通项公式;(2)若数列
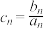 ,求数列
,求数列 的前
的前 项和
项和 .
.
您最近一年使用:0次
2020-11-04更新
|
2062次组卷
|
5卷引用:新疆乌鲁木齐市第八中学2020-2021学年高一下学期第一阶段考试数学试题
名校
解题方法
6 . 已知数列 满足
满足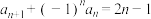 ,则数列
,则数列 的前32项之和为
的前32项之和为__________ .
 满足
满足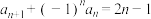 ,则数列
,则数列 的前32项之和为
的前32项之和为
您最近一年使用:0次
2020-11-02更新
|
2696次组卷
|
7卷引用:新疆实验中学2021届高三11月月考数学试题
新疆实验中学2021届高三11月月考数学试题安徽省亳州市蒙城第一中学东校区2022-2023学年高三上学期第四次月考数学试题贵州省遵义市2021届高三上学期第一次联考理科数学试题(已下线)第23练 数列的通项与求和-2021年高考数学(文)一轮复习小题必刷(已下线)第24练 数列的通项与求和-2021年高考数学(理)一轮复习小题必刷(已下线)热点06 数列-2021年高考数学【热点·重点·难点】专练(山东专用)宁夏石嘴山市2022届高三适应性测试数学(理)试题
名校
解题方法
7 . 在等差数列 中,已知
中,已知
(1)求 的通项公式;
的通项公式;
(2)令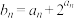 ,求
,求 的前
的前 项和
项和 .
.
 中,已知
中,已知
(1)求
 的通项公式;
的通项公式;(2)令
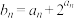 ,求
,求 的前
的前 项和
项和 .
.
您最近一年使用:0次
2020-06-03更新
|
329次组卷
|
2卷引用:新疆维吾尔自治区乌鲁木齐市第八十中学2024届高三上学期11月月考数学试题
名校
8 . 等差数列 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则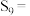 ( ).
( ).
 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则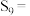 ( ).
( ).| A.39 | B.29 | C.28 | D.24 |
您最近一年使用:0次
2020-04-29更新
|
946次组卷
|
3卷引用:新疆博尔塔拉蒙古自治州第五师高级中学2019-2020学年高二上学期第一次月考数学试题
解题方法
9 . 设 是公差不为零的等差数列
是公差不为零的等差数列 的前n项和.已知
的前n项和.已知 是
是 与
与 的等比中项,
的等比中项, .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求
,求 的前n项和
的前n项和 .
.
 是公差不为零的等差数列
是公差不为零的等差数列 的前n项和.已知
的前n项和.已知 是
是 与
与 的等比中项,
的等比中项, .
.(Ⅰ)求
 的通项公式;
的通项公式;(Ⅱ)设
 ,求
,求 的前n项和
的前n项和 .
.
您最近一年使用:0次
2020-04-23更新
|
249次组卷
|
2卷引用:新疆维吾尔自治区2019-2020学年高三适应性检测(文科)数学(问卷)试题
名校
解题方法
10 . 已知 是递增的等差数列,
是递增的等差数列, 且
且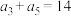 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设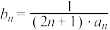 ,求数列
,求数列 的前n项和
的前n项和 .
.
 是递增的等差数列,
是递增的等差数列, 且
且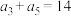 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
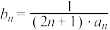 ,求数列
,求数列 的前n项和
的前n项和 .
.
您最近一年使用:0次
2020-03-26更新
|
342次组卷
|
3卷引用:新疆维吾尔自治区乌鲁木齐市第十一中学2024届高三上学期12月月考数学试题



